[数据结构与算法]数据结构——队列

队列

队列是一个插入操作和删除操作受到限制的线性表数据结构。队列的插入和删除被限制在表的两端，即插入操作只能在表的一端进行，而删除操作只能在表的另一端进行，因此队列又称先进先出表。

顺序存储的队列

队列既可以采用顺序存储，也可以采用链接存储来实现。下面给出了一种基于顺序存储的队列实现方案：

该队列存储了 4 个元素 {56,77,15,12} ，其中 56 为队列头， 12 为队列尾。

这种实现方案将队列元素存储在一片连续的空间中，并通过data、front、rear和max四个属性元素组织成为一个结构：

• data: 给出队列存储空间的起始地址；
• front: 为队头指针，它指向队头元素；
• rear: 为队尾指针，它指向下一个入队元素的存储位置；
• max: 指明队列存储空间中最多可存储的数据元素个数。（通常为了区分队列空和满，会在队列尾留一个空数据单元，此时队列最多可放max-1个数据元素）

特别说明：空间的开始地址为data，连续空间里的位置编号从data所指的开始位置起，到该空间的结束位置，编号依次是0,1,2,…,max-1。在图1的示例中max=6。下一个出队元素（这里是队列的头结点）所存储的位置编号用front给出，下一个入队元素应存储的位置编号用rear给出。

基于这些属性要素组织成的队列结构如下所示：

struct SeqQueue {
    T* data; // 指向数据元素数组的指针
    int front; // 下一个出队元素的数组下标
    int rear; // 下一个入队元素应该存放的单元的数组下标
    int max;  // 队列中最多可放max-1个数据元素，留一个空数据单元以区分空和满
};

为了大家更好地理解队列空、队列满以及入队和出队操作，相关知识介绍如下：

• 队列为空的判断：当front与rear相等时，队列为空。
• 队列为满的判断：当front=0,rear=max-1或者front=rear+1（相当于实现了循环）时，队列为满。
• 出队操作：出队操作的前提是队列不为空。每出队一个元素（将front处的元素出队），就将front加 1 ；加 1 后，如果front超出最后一个位置max-1，就将front重新设置为 0 。

同时为了讨论简单，我们假设队列元素的数据类型为整数：

typedef int T; // 队列元素的数据类型

据此，只要给定指向该结构的一指针sq，就可对队列进行出队入队操作。

• 在给定图1的状态下，连续 2 次出队操作，这时的状态则变为如图 2 所示的状态。
  
• 在给定图 2 的状态下，连续 2 次入队操作（依次入队 23 、78 ），这时的状态则如图 3 所示。
  

顺序队列的主要操作

对数据元素进行操作处理是一个数据结构的重要组成部分。队列涉及的主要操作如下:

• 创建队列：创建一个最多可以存储maxlen个元素的顺序队列。具体操作函数定义如下：
  SeqQueue* SQ_Create(int maxlen)；
• 释放队列空间：释放队列所占用的空间，以删除队列。具体操作函数定义如下：
  void SQ_Free(SeqQueue* sq)；
• 置空队列：将队列置空。具体操作函数定义如下：
  void SQ_MakeEmpty(SeqQueue* sq)；
• 判断队列是否为空：若队列为空，则返回true，否则返回false。具体操作函数定义如下：
  bool SQ_IsEmpty(SeqQueue* sq)；
• 判断队列是否为满：若队列满，则返回true，否则返回false。具体操作函数定义如下：
  bool SQ_IsFull(SeqQueue* sq)；
• 求队列长度：获取队列的长度。具体操作函数定义如下：
  int SQ_Length(SeqQueue* sq)；
• 将元素 x 入队：将 x 入队，若入队失败(队列满)，则返回false，否则返回true。具体操作函数定义如下：
  bool SQ_In(SeqQueue* sq, T x)；
• 从队列sq出队一个元素：item为出队的元素的值。若出队成功(队列不为空)，则返回true；否则(队列空)，返回false，此时item不会返回有效值。具体操作函数定义如下：
  bool SQ_Out(SeqQueue* sq, T& item)；
• 获取队列头结点元素：返回时head保存头结点元素。若获取失败(队列空)，则返回值为false，否则返回值为true。具体操作函数定义如下：
  bool SQ_Head(SeqQueue* sq, T& head)；
• 打印队列元素：依次打印出队列中的每个元素。具体操作函数定义如下：
  void SQ_Print(SeqQueue* sq)。

// 循环顺序的队列实现文件

#include <stdio.h>
#include <stdlib.h>

typedef int T; // 队列元素的数据类型

struct SeqQueue {
    T* data;//指向数据元素数组的指针
    int front;//下一个出队元素的数组下标
    int rear;//下一个入队元素应该存放单元的数组下标
    int max;//队列中最多可以存放max-1个元素，留下一个空数据单元以区分空和满
};

SeqQueue* SQ_Create(int maxlen)
// 创建顺序队列, 队列最多存储maxlen个队列元素。
{
    SeqQueue* sq = (SeqQueue*)malloc(sizeof(SeqQueue));
    sq->data = (T*)malloc(sizeof(T) * (maxlen + 1));
    sq->front = sq->rear = 0;
    sq->max = maxlen + 1;
    return sq;
}

void SQ_Free(SeqQueue* sq)
// 释放队列空间，以删除队列。
{
    free(sq->data);
    free(sq);
}

void SQ_MakeEmpty(SeqQueue* sq)
// 将队列置空。
{
    sq->front = 0;
    sq->rear = 0;
}

bool SQ_IsEmpty(SeqQueue* sq)
// 判断队列是否为空，为空返回true，否则返回false。
{
    if (sq->front == sq->rear) {
        return true;
    }
    return false;
}

bool SQ_IsFull(SeqQueue* sq)
// 判断队列是否为满。为满返回true,否则返回false。
{
    if ((sq->front == 0 && sq->rear == sq->max - 1) || sq->front == sq->rear + 1) {
        return true; //front=rear+1相当于循环
    }
    else {
        return false;
    }
}

int SQ_Length(SeqQueue* sq)
// 队列长度。
{
    if (sq->front <= sq->rear) {
        return sq->rear - sq->front;
    }
    else {
        return sq->max - (sq->front - sq->rear);
    }    

}

bool SQ_In(SeqQueue* sq, T x)
// 将x入队。若入队失败(队列满)，则返回false，否则返回true。
{
    if (SQ_IsFull(sq)) {
        return false;
    }
    else {
       sq->data[sq->rear++]=x;
       if (sq->rear == sq->max) {//实现循环
           sq->rear = 0;
       }
       return true;
    }

}

bool SQ_Out(SeqQueue* sq, T& item)
// 从队列sq出队一个元素，返回时item为出队的元素的值。
// 若出队成功(队列不为空)，则返回true，否则(队列空)，返回false，
// 此时item不会返回有效值。
{
    if (SQ_IsEmpty(sq)) {
        return false;
    }
    else {
        item = sq->data[sq->front];
        sq->front++;
        if (sq->front == sq->max) {
            sq->front = 0;
        }
        return true;
    }

}

bool SQ_Head(SeqQueue* sq, T& head)
// 获取队列头结点元素，返回时head保存头结点元素。
// 若获取失败(队列空)，则返回值为false，否则返回值为true。
{
    if (SQ_IsEmpty(sq)) {
        return false;
    }
    else {
        head = sq->data[sq->front];
        return true;
    }
}

void SQ_Print(SeqQueue* sq)
// 依次打印出队列中的每个元素。
{
    int i = sq->front;
    if (SQ_IsEmpty(sq)) {
        printf("queue is emtpy");
        return;
    }
    for (i = sq->front; i != sq->rear; i = (i + 1) % sq->max) {
        printf("%d  ", sq->data[i]);
    }
    printf("\n");
}

链式队列

队列的存储除了顺序存储之外也可以采用链接存储方式来实现。图 1 描述了队列的一种链接存储实现方案。

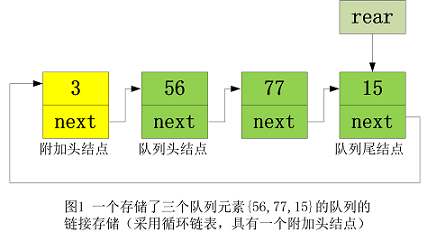
该队列存储了 3 个元素 {56,77,15} ，其中 56 为队列头， 15 为队列尾。

这种实现方案中涉及到的两个属性元素如下：

• rear: 指向队列尾结点的指针；
• next: 指向队列头结点的指针。

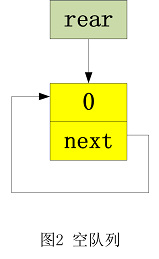
当队列是空队列时，rear指向附加头结点，附加头结点的数据项等于 0 ，如图 2 所示。

基于这些属性要素组织成的链表结点的结构定义为：

struct LNode {
    T data;
    LNode* next;
};

为了讨论简单，我们假设队列元素的数据类型为整数：

typedef int T; // 队列元素的数据类型

据此，只要给定rear指针，我们就可以对队列进行入队和出队的操作。

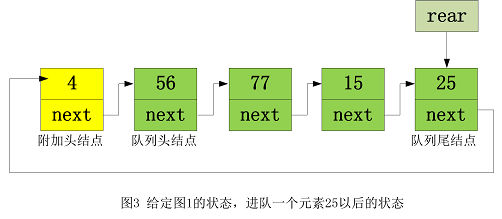
• 在给定图 1 的状态下，进队一个元素 25 以后的状态如图 3 所示：
  
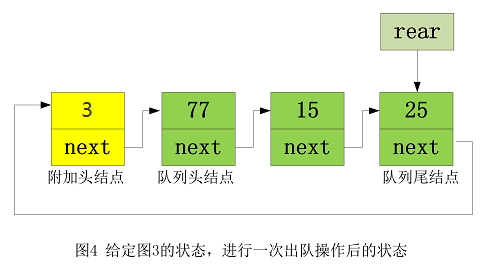
• 若出队一个元素是指将当前队列头结点去掉。则在给定图 3 的状态下，进行一次出队后的状态如图 4 所示：
  

链式队列的主要操作

对数据元素进行操作处理是一个数据结构的重要组成部分。队列涉及的主要操作如下：

• 创建队列：创建一个队列。具体操作函数定义如下：
  LNode* CLQ_Create()；
• 释放队列空间：释放队列所占用的空间，其中rear指向尾结点。具体操作函数定义如下：
  void CLQ_Free(LNode* rear)；
• 置空队列：将队列变为空队列，其中rear指向尾结点。具体操作函数定义如下：
  void CLQ_MakeEmpty(LNode* & rear)；
• 判断队列是否为空：若队列为空，则返回 true，否则返回false。具体操作函数定义如下：
  bool CLQ_IsEmpty(LNode* rear)；
• 求队列长度：获取队列的长度，其中rear指向尾结点。具体操作函数定义如下：
  int CLQ_Length(LNode* rear)；
• 新结点入队列：新结点加入链表尾部，其中rear指向尾结点。具体操作函数定义如下：
  void CLQ_In(LNode* & rear, T x)；
• 队列元素出队列：item为出队的元素的值。若出队成功(队列不为空)，则返回true；否则(队列空)，返回false。具体操作函数定义如下：
  bool CLQ_Out(LNode* & rear, T& item)；
• 获取队列头结点元素：若获取失败(队列空)，则返回值为false，否则返回值为true。具体操作函数定义如下：
  bool CLQ_Head(LNode* rear, T& item)；
• 打印队列：依次打印出队列中的每个元素。具体操作函数定义如下：
  void CLQ_Print(LNode* rear)。

// 队列的链接存储实现文件。
// 采用循环链表，具有附加头节点，使用尾结点指针。
// CLQ_   Circularly Linked Queue

#include <stdio.h>
#include <stdlib.h>

typedef int T;//队列元素的数据类型

struct LNode {
    T data;
    struct LNode* next;
};


LNode* CLQ_Create()
// 创建一个队列。
{
    LNode* rear = (LNode*)malloc(sizeof(LNode));
    rear->data = 0;//头结点的数据域，即元素个数为0
    rear->next = rear;//循环列表
    return rear;
}
void CLQ_Free(LNode* rear)
// rear指向尾结点。
{
    CLQ_MakeEmpty(rear);
    free(rear);
}

void CLQ_MakeEmpty(LNode*& rear)
// rear指向尾结点。
// 将队列变为空队列。
{
    T item;
    while (!CLQ_IsEmpty(rear))
        CLQ_Out(rear, item);
}

bool CLQ_IsEmpty(LNode* rear)
// 判断队列是否为空。
{
    return rear == rear->next;
}

int CLQ_Length(LNode* rear)
// 返回队列长度，rear指向尾结点。
{
    return rear->next->data;
}

void CLQ_In(LNode*& rear, T x)
// 入队列, 新结点加入链表尾部。rear指向尾结点。
{
    struct LNode* newNode = (LNode*)malloc(sizeof(LNode));
    newNode->data = x;
    newNode->next = rear->next;
    rear->next = newNode;
    rear = newNode;
    rear->next->data++;
}

bool CLQ_Out(LNode*& rear, T& item)
// 出队列。空队列时，返回值为false。rear指向尾结点。
{
    if (CLQ_IsEmpty(rear)) {
        return false;
    }
    else if (rear->next->data == 1) {
        free(rear);
        rear = rear->next;
        rear->next = rear;
        rear->data = 0;
    }
    else {
        LNode* front = rear->next->next;//不是头结点，而是首元结点
        rear->next->next = front->next;
        item = front->data;
        free(front);
        front = NULL;
        rear->next->data--;
        return true;
    }
}

bool CLQ_Head(LNode* rear, T& item)
// rear指向尾结点。
// 获取队列头。空队列时返回值为false。
{
    if (CLQ_IsEmpty(rear))
        return false;

    item = rear->next->next->data;
    return true;
}
void CLQ_Print(LNode* rear)
// 打印队列。
{
    if (CLQ_IsEmpty(rear)) {
        printf("The queue is: empty. \n");
        return;
    }
    LNode* node = rear->next->next;
    do {
        printf("%d  ", node->data);
        node = node->next;
    } while (node != rear->next);
    //printf("\n");
}