[数据结构与算法][AGC006B] Median Pyramid Easy(题解)

一道挺有意思的构造题

其实有很多种构造方法，这里介绍一种比较好想的方法。

我们想让 $x$ 作为最顶层的元素，最好的方法就是让 $x$ 一直处于中间。于是我们就可以使得 $x$ 左右两边的数都比 $x$ 小，分别为 $x?1$ 和 $x+1$,如图
（有点难看）

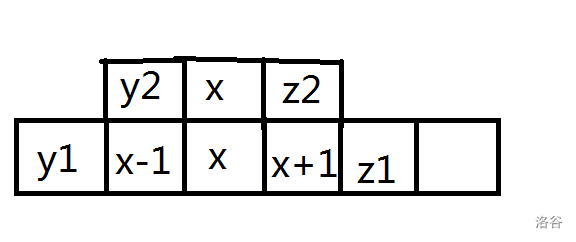
这里我们可以证明一下 $x$ 一直处在中间

若 $y1>=x$ 则 $y2=x$

若 $y1<x$ 则 $y2=x?1$

所以 $y2=$ $x$ 或 $x?1$

同理

若 $z1<=x$ 则 $z2=x$

若 $y1>x$ 则 $y2=x+1$

所以 $z2=$ $x$ 或 $x+1$

综上，无论 $y2$ 和 $z2$ 怎么搭配，中间的数一定是 $x$

所以我们写程序的时候只用将 $x?1,x,x+1$ 放在中间即可，其他的数可以随便放置

对于无法构造的情况我们只需判断 $x$ 是否等于 $1$ 或 $2\times n+1$

完整代码

#include <cstdio>
int a[200005], tot = 1;
int main() {
	int n, x;
	scanf("%d %d", &n, &x);
	if (x == 1 || x == 2 * n - 1) {
		printf("No");
		return 0;
	}
	printf("Yes\n");
	a[n - 1] = x - 1, a[n] = x, a[n + 1] = x + 1;
	for (int i = 1; i <= n - 2;) {
		if (tot == x - 1 || tot == x || tot == x + 1) tot++;
		else a[i] = tot, tot++, i++;
	}
	for (int i = n + 2; i <= 2 * n - 1;) {
		if (tot == x - 1 || tot == x || tot == x + 1) tot++;
		else a[i] = tot, tot++, i++;
	}
	for (int i = 1; i <= 2 * n - 1; i++) {
		printf("%d\n", a[i]);
	}
	return 0;
}