什么是决策树

decision tree决策树是一种基本的分类和回归方法。顾名思义，决策树模型呈树形结构，就是数据结构中的树，有一个根节点、若干个内部节点、若干个叶子节点（决策结果）。

在分类问题中： 决策树可以认为是if-then规则的集合；也可以认为是定义在特征空间与类空间上的条件概率分布。
在回归问题中： 决策树可看作将空间用超平面进行划分，每内部节点都将当前的空间一分为二，使得每个叶子节点都是空间中的一个不相交的区域。

模型优点： 具有可读性、分类深度快、可以处理数值和非数值字段
模型缺点： 容易过拟合、无法学习属性之间的相关性

决策树学习包括3个步骤：
①特征选择
②决策树的生成
③决策树的修剪

3种决策树

介绍ID3决策树、C4.5决策树、CART决策树

ID3决策树（Iterative Dichotomiser）

熵(entropy)

熵在信息论中表示随机变量不确定性的度量。
熵越大，随机变量的不确定性就越大。
信息熵的定义：
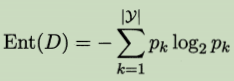
在这里插入图片描述
二分类中当p=0或p=1时信息熵等于0，此时没有不确定性。而当p=0.5时，信息熵取值最大等于1，随机变量不确定性最大。

信息增益

计算出信息熵后，再考虑到不同的分支节点所包含的样本数不同，给分支节点赋予权重|Dv|/|D|，即样本数越多的分支节点的影响越大。

信息增益定义如下：
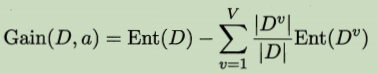
在这里插入图片描述
决策树学习中的信息增益等价于训练数据集中类与特征的互信息（熵与条件熵的差）

信息增益越大，意味着使用属性a来进行划分所获得的“纯度提升”越大。因此可以用信息增益最大的属性来进行决策树的划分。ID3决策树就是以信息增益为准则来学习的。

C4.5决策树

增益率

由于信息增益对可取值数目较多的属性有所偏好，挥带来不利的影响。因此引入“增益率”：

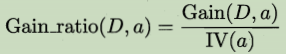
在这里插入图片描述
其中

（这里的IV(a)我觉得像熵一样），当属性a的可能取值数目越多，IV(a)越大。

但是增益率准则对可取值数目较少的属性有所偏好，因此C4.5算法并不是直接选择增益率最大的候选划分属性，而是使用了一个启发式：先从候选划分属性中找出信息增益高于平均水平的属性，再从中选择增益率最高的

CART决策树(Classification And Regression Tree)

基尼指数(Gini index)

基尼指数可以用于度量数据集D的纯度，定义如下：
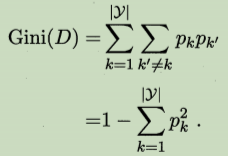
在这里插入图片描述
Gini(D)反映了从数据集D中随机抽取两个样本，其类别标记不一致的概率，Gini(D)越小，纯度越高。

属性a的基尼指数的定义：
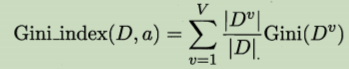
在这里插入图片描述

选择划分后，基尼指数最小的属性作为最优划分属性。

训练过程

从根节点开始进行递归操作，构建二叉决策树：
①设节点的训练数据集为D，计算现有特征对该数据集的基尼指数，对每个特征A的可能取值a进行测试，将是否等于a划分成D1和D2两个数据集，计算A=a时的基尼指数。
②再所有可能的特征A以及它们所有可能的切分点a中，选择基尼指数最小的特征机器对应的切分点作为最优特征与最优切分点，按该节点进行数据集分配到两个子节点中。
③对两个子节点递归调用①②直至满足停止条件：节点中的用本个数小于预定阈值或当前数据集的基尼指数小于预定阈值或没有其他特征

剪枝

剪枝(pruning)时决策树应对过拟合的方法，主要有预剪枝(prepruning)和后剪枝(post-pruning)。加入西瓜书上的例子：

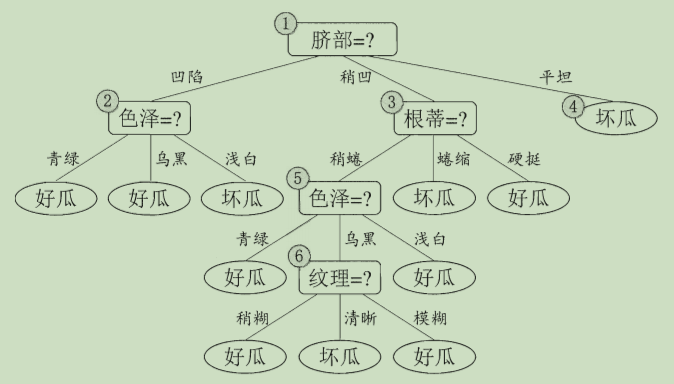
不剪枝：
在这里插入图片描述

①预剪枝： 再决策树生成过程中，对每个节点的划分前先进行估计，若当前节点的划分不能带来决策树泛化能力的提升，则停止划分并将当前节点标记为叶子节点。
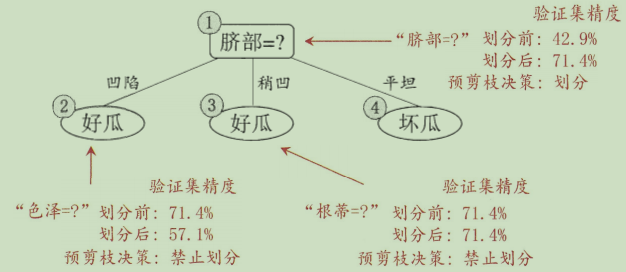
在这里插入图片描述
优点：不仅能降低过拟合的风险，害显著减少了决策树的训练时间和预测时间。
缺点：一些分支再当前可能不能提升泛化能力，但是后续划分也有可能让泛化性能显著提升，因此预剪枝存在欠拟合的风险。

②后剪枝： 先从训练集生成依课完整的决策树，然后自底向上对非叶子节点进行考察，若将该节点对应的子树替换为叶节点能带来决策树泛化能力的提升，则将该子树替换为叶节点。
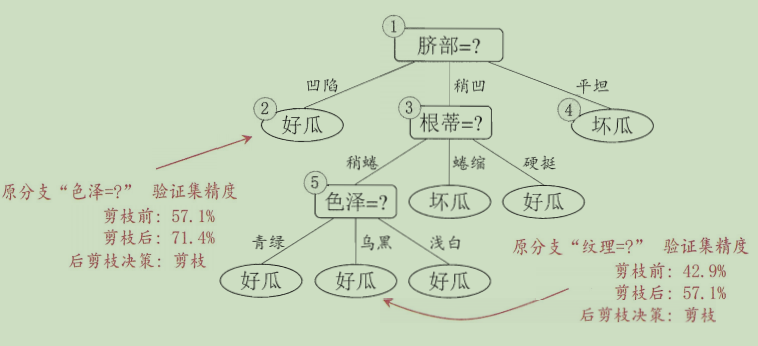
在这里插入图片描述
优点：后剪枝的欠拟合风险很小，泛化能力往往优于预剪枝的决策树。
缺点：后剪枝时再完全展开决策树后再自底向上进行考察，训练时间比预剪枝大很多。