回归问题：目标值是连续型值的问题。
线性回归：通过一个或者多个自变量与因变量之间之间进行建模的回归分析，其中特点为一个或多个称为回归系数的模型参数的线性组合。
from sklearn import linear_model一元线性回归：涉及到的变量只有一个
多元线性回归：涉及到的变量两个或两个以上
通用公式：
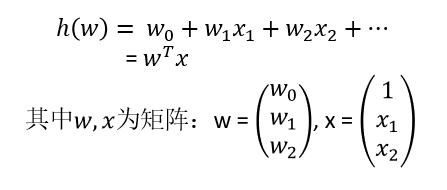
其中，w为权重，x为特征，w0为偏移量。
预测结果与真实值会有误差，使用损失函数定义：
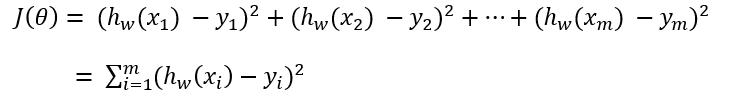
其中，yi为第i个训练样本的真实值，hw(xi)为第i个训练样本特征值组合预测函数，即误差的平方和，又称为最小二乘法。
1. 正规方程
from sklearn.linear_model import LinearRegression
其中，X为特征值矩阵，y为目标值矩阵。
优点：可以经过一次运算得出，不需要多次迭代；对于数量较小的数据预测精确度较高。
缺点：当特征过于复杂，求解速度太慢；对于复杂的算法，不能使用正规方程求解；只适用于线性模型。
例1：波士顿房价案例
需求：根据给出的信息，使用正规方程预测波士顿房价。
from sklearn.datasets import load_boston
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
# 获取数据
lb = load_boston()
# 分割数据集到训练集和测试集
x_train, x_test, y_train, y_test = train_test_split(lb.data, lb.target, test_size=0.25)
# 特征值和目标值是都必须进行标准化处理, 实例化两个标准化API
std_x = StandardScaler()
x_train = std_x.fit_transform(x_train)
x_test = std_x.transform(x_test)
# 目标值
std_y = StandardScaler()
y_train = std_y.fit_transform(y_train.reshape(-1, 1))
y_test = std_y.transform(y_test.reshape(-1, 1))
# estimator预测
# 正规方程求解方式预测结果
lr = LinearRegression()
lr.fit(x_train, y_train)
print("回归系数：", lr.coef_)
y_lr_predict = std_y.inverse_transform(lr.predict(x_test))
print("正规方程测试集里面每个房子的预测价格：", y_lr_predict)
输出：
回归系数： [[-0.08438297? 0.12662503? 0.00617453? 0.08445922 -0.17802891? 0.31122427
? -0.02547949 -0.33519079? 0.29937768 -0.25666255 -0.20903889? 0.1118847
? -0.38413983]]
正规方程测试集里面每个房子的预测价格： [[29.23338548]
?[ 8.8447294 ]
?[16.88213279]
?[28.68269785]
?[13.82717473]...
[21.05746016]
?[34.16472524]
?[13.79114495]
?[29.78022612]
?[25.79496649]]
2. 梯度下降
from sklearn.linear_model import SGDRegressor
我们以单变量中的w0,w1为例子：
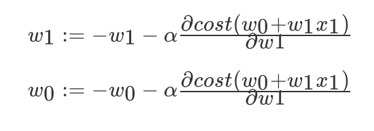
其中，α为学习速率，需要手动指定；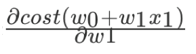
表示方向。沿着这个函数下降的方向找，最后就能找到山谷的最低点，然后更新w值。梯度下降优化方法常用于训练数据规模十分庞大的任务。
优点：对于大规模数据预测精确度较高，适用于线性模型、逻辑回归等各种类型的模型。
缺点：需要选择学习率α；需要多次迭代。
例2：将上面的波士顿房价案例使用梯度下降的方法预测。
from sklearn.datasets import load_boston
from sklearn.linear_model import SGDRegressor
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
# 获取数据
lb = load_boston()
# 分割数据集到训练集和测试集
x_train, x_test, y_train, y_test = train_test_split(lb.data, lb.target, test_size=0.25)
# 特征值和目标值是都必须进行标准化处理, 实例化两个标准化API
std_x = StandardScaler()
x_train = std_x.fit_transform(x_train)
x_test = std_x.transform(x_test)
# 目标值
std_y = StandardScaler()
y_train = std_y.fit_transform(y_train.reshape(-1, 1))
y_test = std_y.transform(y_test.reshape(-1, 1))
# 梯度下降去进行房价预测
sgd = SGDRegressor()
sgd.fit(x_train, y_train)
print("回归系数：", sgd.coef_)
# 预测测试集的房子价格
y_sgd_predict = std_y.inverse_transform(sgd.predict(x_test))
print("梯度下降测试集里面每个房子的预测价格：", y_sgd_predict)输出：
回归系数： [-0.08941871? 0.08789607 -0.04447809? 0.07226135 -0.15867807? 0.27921188
?-0.00412562 -0.28211046? 0.13217807 -0.08845703 -0.2132474?? 0.09144371
?-0.44183021]
梯度下降测试集里面每个房子的预测价格： [21.11741232? 8.45862731 21.73867322 20.46478787 14.76453375 ... 41.72498704 26.45385124 18.12149835 23.03475815
?23.38007714]
3. 回归性能评估
均方误差（Mean Squared Error，MSE）评价机制：每一个样本误差的平方和除以样本数。
from sklearn.metrics import mean_squared_error
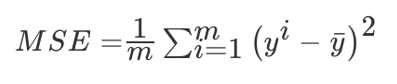
?其中，yi为预测值，y_bar为真实值。
mean_squared_error(y_true, y_pred) 均方误差回归损失
参数：
y_true：真实值
y_pred：预测值
返回值：浮点数结果
计算例1的均方误差：
print("正规方程的均方误差：", mean_squared_error(std_y.inverse_transform(y_test), y_lr_predict))输出：
正规方程的均方误差： 20.510530562954916
?计算例2的均方误差：
print("梯度下降的均方误差：", mean_squared_error(std_y.inverse_transform(y_test), y_sgd_predict))输出：
梯度下降的均方误差： 19.560352040811527
4. 过拟合与欠拟合
过拟合：一个假设在训练数据上能够获得比其他假设更好的拟合，但是在训练数据外的数据集上却不能很好地拟合数据，此时认为这个假设出现了过拟合的现象。
过拟合的原因通常为模型过于复杂，存在一些嘈杂特征，解决方法包括交叉验证、正则化、消除多项式中的过高次项等。
欠拟合：一个假设在训练数据上不能获得更好的拟合，但是在训练数据外的数据集上也不能很好地拟合数据，此时认为这个假设出现了欠拟合的现象。
欠拟合的原因通常为模型过于简单，解决方法为增加数据的特征数量。
5. 岭回归
岭回归是带有正则化的线性回归，可以较好地解决过拟合的问题。
from sklearn import linear_model.Ridge
L2正则化的作用：可以使得W的每个元素都很小，都接近于0。
优点：越小的参数说明模型越简单，越简单的模型则越不容易产生过拟合现象。
sklearn.linear_model.Ridge(alpha=1.0) 具有L2正则化的线性最小二乘法
参数：
alpha：正则化力度
返回值coef_属性：回归系数
例3：将上面的波士顿房价案例使用岭回归的方法预测。
from sklearn.datasets import load_boston
from sklearn.linear_model import Ridge
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
# 获取数据
lb = load_boston()
# 分割数据集到训练集和测试集
x_train, x_test, y_train, y_test = train_test_split(lb.data, lb.target, test_size=0.25)
# 特征值和目标值是都必须进行标准化处理, 实例化两个标准化API
std_x = StandardScaler()
x_train = std_x.fit_transform(x_train)
x_test = std_x.transform(x_test)
# 目标值
std_y = StandardScaler()
y_train = std_y.fit_transform(y_train.reshape(-1, 1))
y_test = std_y.transform(y_test.reshape(-1, 1))
# 岭回归去进行房价预测
rd = Ridge(alpha=1.0)
rd.fit(x_train, y_train)
print(rd.coef_)
# 预测测试集的房子价格
y_rd_predict = std_y.inverse_transform(rd.predict(x_test))
print("岭回归测试集里面每个房子的预测价格：", y_rd_predict)
print("岭回归的均方误差：", mean_squared_error(std_y.inverse_transform(y_test), y_rd_predict))
输出：
[[-0.13628067? 0.16330066 -0.00630566? 0.06523728 -0.20412496? 0.25113994
?? 0.0801901? -0.33633465? 0.30667812 -0.20033917 -0.22404729? 0.09775338
? -0.45382174]]
岭回归测试集里面每个房子的预测价格： [[17.4491666 ]
?[20.50750154]
?[33.92237846]
?[19.86748357]
?[15.94954384]...
[22.40077728]
?[-5.35978023]
?[27.07257406]
?[18.69425565]
?[ 3.49050573]]
岭回归的均方误差： 19.826138761003797