题目链接2021牛客暑期多校训练营2 F Girlfriend
数学题
意思就是求两个球相交部分的体积
上代码
#include <bits/stdc++.h>
using namespace std;
const double PI = acos(-1);
//坐标
struct pos
{
double x,y,z;
};
//输入数据
int T;
pos p[5];
double k1,k2;
//由两球球心和半径得到其相交部分体积
void calc(pos o1,pos o2,double r1,double r2)
{
double ans=0.0;
double dis=sqrt((o1.x-o2.x)*(o1.x-o2.x)+(o1.y-o2.y)*(o1.y-o2.y)+(o1.z-o2.z)*(o1.z-o2.z));
//不相交
if(dis>=r1+r2)
ans=0;
//内含
else if (dis+r1<=r2)
ans=(4.00/3.00)*PI*r1*r1*r1;
else if(dis+r2<=r1)
ans=(4.00/3.00)*PI*r2*r2*r2;
else
{
//余弦定理
double cos_r1_dis=(r1*r1+dis*dis-r2*r2)/(2.0*dis*r1);
//计算球缺的高度
double h1=r1-r1*cos_r1_dis;
//球缺体积计算公式
ans+=PI*h1*h1*(r1-h1/3.0);
//余弦定理
double cos_r2_dis=(r2*r2+dis*dis-r1*r1)/(2.0*dis*r2);
//计算球缺的高度
double h2=r2-r2*cos_r2_dis;
//球缺体积计算公式
ans+=(PI*h2*h2*(r2-h2/3.0));
}
printf("%.3f\n",ans);
}
int main()
{
cin>>T;
while(T--)
{
for(int i = 0; i < 4; i++)
cin >> p[i].x >> p[i].y >> p[i].z;
cin>>k1>>k2;
double tmp1=k1*k1-1,tmp2=k2*k2-1;
pos O1,O2;
double r1,r2,D1,D2;
//球1
O1.x=(k1*k1*p[1].x-p[0].x)/tmp1;
O1.y=(k1*k1*p[1].y-p[0].y)/tmp1;
O1.z=(k1*k1*p[1].z-p[0].z)/tmp1;
D1=k1*k1*(p[1].x*p[1].x+p[1].y*p[1].y+p[1].z*p[1].z)-p[0].x*p[0].x-p[0].y*p[0].y-p[0].z*p[0].z;
D1/=tmp1;
r1=sqrt(O1.x*O1.x+O1.y*O1.y+O1.z*O1.z-D1);
//球2
O2.x=(k2*k2*p[3].x-p[2].x)/tmp2;
O2.y=(k2*k2*p[3].y-p[2].y)/tmp2;
O2.z=(k2*k2*p[3].z-p[2].z)/tmp2;
D2=k2*k2*(p[3].x*p[3].x+p[3].y*p[3].y+p[3].z*p[3].z)-p[2].x*p[2].x-p[2].y*p[2].y-p[2].z*p[2].z;
D2/=tmp2;
r2=sqrt(O2.x*O2.x+O2.y*O2.y+O2.z*O2.z-D2);
//printf("o1: %lf %lf %lf r1= %lf\n",O1.x,O1.y,O1.z,r1);
//printf("o2: %lf %lf %lf r2= %lf\n",O2.x,O2.y,O2.z,r2);
calc(O1,O2,r1,r2);
}
return 0;
}
对题目抽象可得这样两个方程
( k12 - 1 ) ( x2 + y2 + z2 ) - ( 2 k12x1 - 2 x0)x - ( 2 k12y1 - 2 y0)y - ( 2 k12z1 - 2 z0)z + k12( x12 + y12 + z12 ) - ( x02 + y02 + z02 ) <= 0
( k22 - 1 ) ( x2 + y2 + z2 ) - ( 2 k22x3 - 2 x2)x - ( 2 k22y3 - 2 y2)y - ( 2 k22z3 - 2 z2)z + k22( x32 + y32 + z32 ) - ( x22 + y22 + z22 ) <= 0
也就是球的一般方程
x2 + y2 + z2 + Ax + By + Cz + D = 0
球的圆心为(-A/2, -B/2, -C/2)
r2为(A2+B2+C2-4D)/4
余弦定理公式来源百度百科
百度百科链接
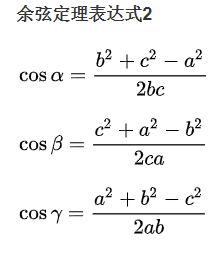
球缺体积公式来源百度百科
百度百科链接

参考了大佬的题解
感谢这位大佬
ta的牛客题解