决策树
算法原理
逻辑:一堆if else 语句的组合
几何:根据某种准测划分特征空间
目的:将样本越分越纯
自信息:I(X)=-logbp(x)
信息熵(自信息的期望):度量随机变量X的不确定性,信息熵越大越不确定
H(X)=E[I(X)]=-∑p(x)logbp(x)(离散型)
ID3决策树
信息熵
信息熵可以度量随机变量X的不确定性,信息熵越大越不确定,可转换到度量样本集合纯度,信息熵越小样本集合的纯度越高。
样本集合?中第?类样本所占比例为pk(k=1,2,…,N)?,则?的信息熵定义为:
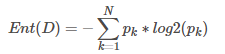
当样本集合中各个类别所占比例相同时(p1=p2=…=pk=1/N????),信息熵达到最大值log2N,纯度最低;
当样本集合中只有类别??的样本,其他类别样本数量为0时?,信息熵达到最小值,纯度最高。
条件熵
条件熵表示的是在已知一个随机变量的条件下, 另一个随机变量的不确定性。假设有随机变量 X 和 Y ,且它们服从以下联合概率分布:

在已知X?的条件下,随机变量Y的条件熵表示,已知X取值xi后,Y的不确定性,计算公式如下:
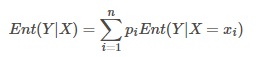

信息增益
信息论中信息增益也称为互信息,其表示已知一个随机变量的信息后使得另一个随机变量的不确定性减少的程度。具体地,假设有随机变量X和Y,那么在已知X的信息后,Y?的不确定性减少的程度为:
I(Y;X)=Ent(Y)-Ent(Y|X)
在已知属性(特征)a的取值后???y的不确定性减少的量,也即纯度的提升,信息增益为:
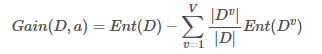
ID3决策树:以信息增益为准则来选择划分属性的决策树。
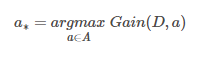
C4.5决策树
增益率

C4.5 算法并不是直接选择增益率最大的候选划分属性,而是使用了一个启发式:
先从候选划分属性中找出信息增益高于平均水平的属性,再从中选择增益率最高的。
CART决策树
CART是Classification and Regression Tree的简称,这是一种著名的决策树学习算法,分类和回归任务都可用。其生成的决策树为二叉树。
CART决策树使用"基尼指数"(Gini index)来选择划分属性。基尼值相对于ID3决策树中的信息熵,而基尼指数相对于ID3决策树中的条件熵。
基尼值
可以用Gini(D)反映了从数据集中随机抽取两个样本,其类别标记不一致的概率。Gini(D)越小,则数据集的纯度越高:
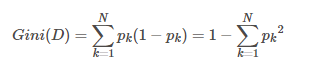
基尼指数
属性a的基尼指数表示在已知属性a的取值后(即在Dv的样本集合中),样本集合D?的基尼值之和,即为:
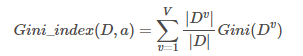
选择基尼指数最小的属性作为最优划分属性:
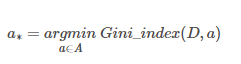
算法流程
-
对每个属性a的每个可能取值v,将数据集D分为a=v和??a≠v两部分来计算基尼指数,即:
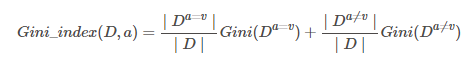
-
选择基尼指数最小的属性及其对应取值作为最优划分属性和最优划分点;
-
重复以上两步,直至满足停止条件。