[数据结构与算法]w1_逻辑回归_理论知识

二分类

1. 计算机的图存储

计算机对图像的存储是用RGB三个矩阵实现的，在实现过程中，用一个非常长的向量来表示列出。对于下面这张图而言，如果我们的图像矩阵是$64\times 64$，那么最终的图像存储的维度将是$64\times 64\times 3=12288$,这里用$n=n_x=12288$来表示向量的维度。

二分分类的目的：对于输入的向量，输出0/1的结果。比如现在这张输入的图，输出0/1表示这张图表示的是否是猫

2. 问题中常用的数据字母表示

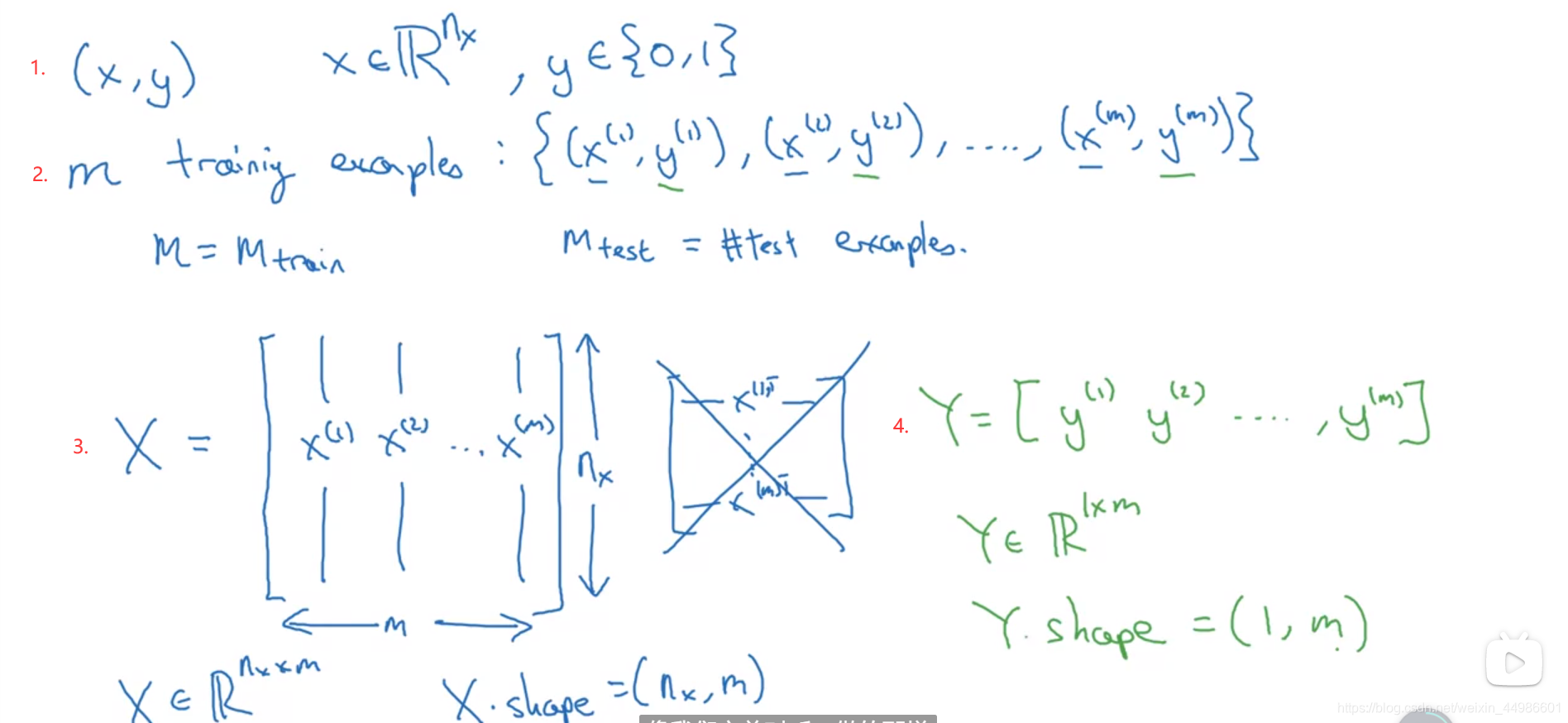
线性回归

1. 符号定义、代价函数与梯度下降法

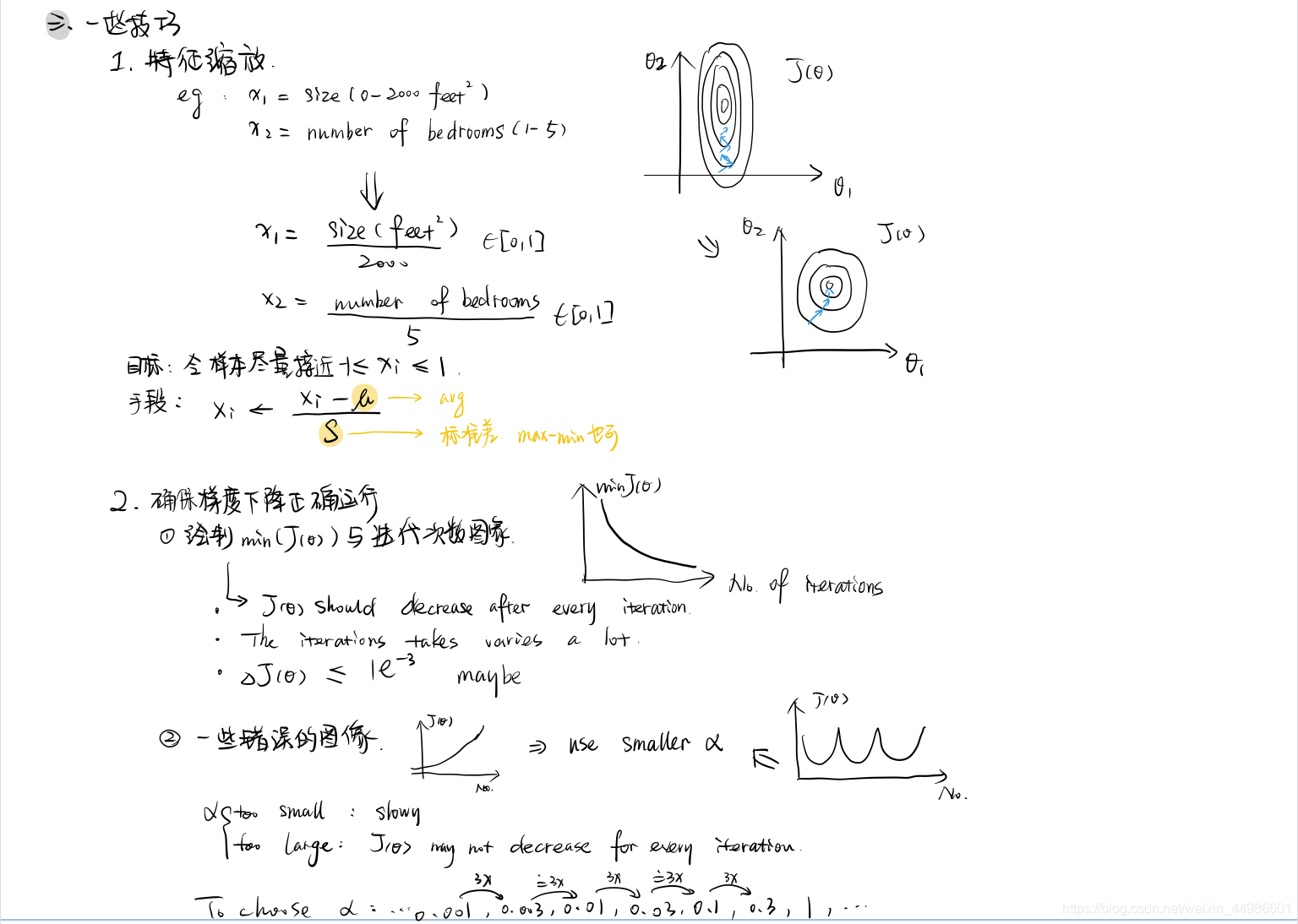
2. 一些技巧

1. 特征缩放时候尽量让所有的特征$x_i$的范围保持在$?1\le x_i\le 1$
2. 可以绘制$min(J_{(\theta )})$与迭代次数$No$的图像，用来确保梯度下降
   

3. 多项式回归的应用

logistics回归算法

logistic回归算法多运用于二分类问题上，即y是离散的情况。

下面的笔记包含了三部分内容

1. 什么是分类问题
2. 分类问题的具体实现（利用decision boundary$?$从数据集中计算得到）
3. 多分类问题的应用（选取其中的一个为一类，剩余的为另一类，依次计算得到boundary。对于不同的boundary得到的值取$max(h_{\theta })$为结果，判断y是0/1）

1. 什么是分类问题

2. 分类问题的具体实现

利用decision boundary$?$从数据集中计算得到
设置阈值，对于计算得到的$h_{\theta }$的值进行划分：

• 大于阈值的y为1
• 小于阈值的y为0

3. 多分类问题的应用

1. 选取其中的一个为一类，剩余的为另一类，依次计算得到boundary。
2. 对于不同的boundary得到的值取$max(h_{\theta })$为结果，判断y是0/1