王道考研 数据结构之树与二叉树
树与二叉树知识点思维导图
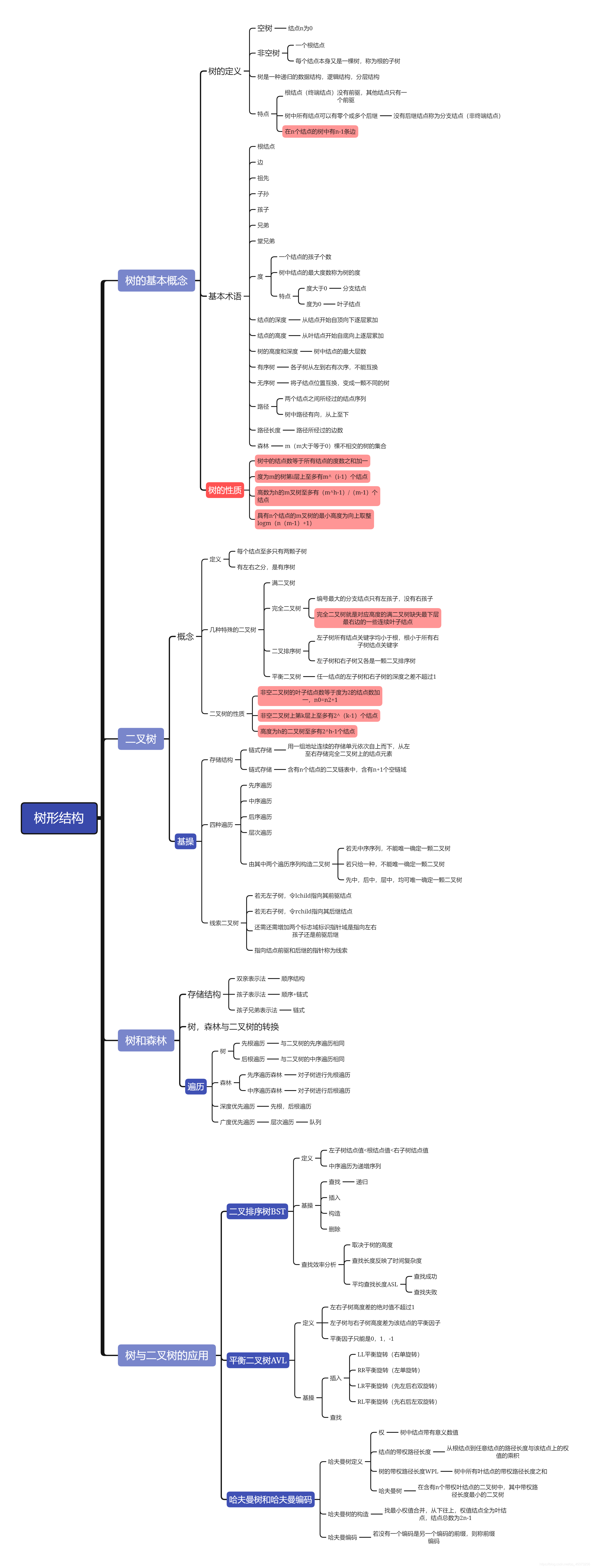
树与二叉树代码实现
1 二叉树
1.1 二叉树的存储结构
-
顺序存储
#define MaxSize 100 struct TreeNode{ ElemType value; //结点中的数据元素 bool isEmpty; //结点是否为空 }; //定义一个数组,按层次存储二叉树的结点 TreeNode t[MaxSize]; for(int i=0;i<MaxSize;i++){ t[i].isEmpty = true; //初始化,所有结点标记为空 } -
链式存储
struct ElemType{ int value; }; typeef struct BiTNode{ ElemType data; //数据域 struct BiTNode *lchild,*rchild; //左右孩子指针 //三叉链表加下面这句,方便找父节点 //struct BiTree *parent; //父节点指针 }BiTNode,*BiTree; //定义一颗空树 BiTree root = NULL; //插入根节点 root = (BiTree) malloc(sizeof(BiTNode)); root->data = {1}; root->lchild = NULL; root->rchild = NULL; //插入新结点 BiTree *p = (BiTree *) malloc(sizeof(BiTNode)); //1.分配空间 p->data = {2}; //2.赋值 p->lchild = NULL; //3.初始化新结点 p->rchild = NULL; root->lchild = p; //4.作为根节点的左孩子n个结点的二叉链表共有n+1个空链域
1.2 二叉树的遍历
递归算法
-
先序遍历(根左右)
void PreOrder(BiTree T){ if(T!=NULL){ visit(T); //访问根节点 reOrder(T->lchild); //递归遍历左子树 PreOrder(T->rchild); //递归遍历右子树 } } -
中序遍历(左根右)
void PreOrder(BiTree T){ if(T!=NULL){ reOrder(T->lchild); //递归遍历左子树 visit(T); //访问根节点 PreOrder(T->rchild); //递归遍历右子树 } } -
后序遍历(左右根)
void PreOrder(BiTree T){ if(T!=NULL){ reOrder(T->lchild); //递归遍历左子树 PreOrder(T->rchild); //递归遍历右子树 visit(T); //访问根节点 } }
上诉三种算法均可转换为非递归算法
非递归算法–中序转换
void InOrder2(BiTree T){
//二叉树中非递归算法用栈
InStack(S); //初始化栈
BiTree p = T; //p是遍历指针
//1.栈不空或p不空时循环
while(p||!isEmpty(S)){
//2.沿根找左孩子,依次入栈,直到左孩子为空
if(p){
Push(S,p); //当前结点入栈
p = p->lchird; //左孩子不为空,一直找左孩子的左孩子的左孩子...
}else{
//3.栈顶元素出栈并访问,遍历右子树
Pop(S,p); //当前结点出栈
visit(p); //访问此结点
p = p->rchild; //右孩子不为空,一直找右孩子的右孩子的右孩子...
}
//4.返回while循环继续if-else
}
}
- 层次遍历
需要借助一个队列void LevelOrder(BiTree T){ InitQueue(Q); //初始化队列 BiTree p; EnQueue(Q,T); //将根节点入队 //1.队列元素不为空则头结点出队,访问此结点 while(!IsEmpty(Q)){ DeQueue(Q,p); //队头元素出队 visit(p); //访问此节点 //2.若左右孩子不为空则将其左右孩子插入队尾,重复上述操作,直到队列为空 if(p->lchild!=NULL) EnQueue(Q,p->lchird); if(p->rchild!=NULL) EnQueue(Q,p->rchild); } }
2 线索二叉树
2.1 线索二叉树的存储结构
typedef struct ThreadNode{
ElemType data; //数据元素
struct ThreadNode *lchild,*rchild; //左右孩子指针
int ltag,rtag; //左右线索标志
}ThreadNode,*ThreadThree;
2.2 线索二叉树的基操
2.2.1 线索二叉树的构造
//中序遍历二叉树,一变遍历一边线索化
void InTread(ThreadTree T){
if(T!=NULL){
InThread(T->lchild);
visit(T);
InThread(T->rchild);
}
}
void visit(ThreadNode *q){
if(q->lchirld == NULL){ //左子树为空,建立前驱线索
q->lchirld = pre;
q->ltag = 1;
}
if(pre!= NULL&&pre->rchild == NULL){ //建立前驱结点的后续线索
pre->rchirld = q;
q->rtag = 1;
}
pre = q;
}
//中序线索化二叉树
void CreatThread(ThreadTree T){
pre = NULL; //pre初始为空
if(T!=NULL){ //非空二叉树才能线索化
InThread(T); //中序线索化二叉树
if(pre->rchild == NULL)
pre->rtag = 1; //处理遍历的最后一个结点
}
}
2.2.2 线索二叉树遍历
- 查找中序前驱遍历二叉树
//找到以p为根的子树中,最后一个被中序遍历的结点 ThreadNode *Lastnode(TheadNode *p){ //循环找到最右下结点(不一定是叶节点) while(p->ltag==0) p=p->rchild; return p; } //在中序线索二叉树中找到结点p的前驱结点 ThreadNode *Prenode(TheadNode *p){ //左子树中最右下结点 if(p->ltag==0) return Lastnode(p->lchild); else return p->lchild; //ltag==1直接返回前驱线索 } //对中序线索二叉树进行逆向中序遍历 void RevInorder(TheadNode *T){ for(ThreadNode *p = Lastnode(T);p!=NULL;p=Prenode(p)) visit(p); } - 查找中序后继遍历二叉树
//找到以p为根的子树中,第一个被中序遍历的结点 ThreadNode *Firstnode(TheadNode *p){ //循环找到最左下结点(不一定是叶节点) while(p->ltag==0) p=p->lchild; return p; } //在中序线索二叉树中找到结点p的后继结点 ThreadNode *Nextnode(TheadNode *p){ //右子树中最左下结点 if(p->rtag==0) return Lastnode(p->rchild); else return p->rchild; //rtag==1直接返回后继线索 } //对中序线索二叉树进行中序遍历(利用线索实现非递归算法) void Inorder(TheadNode *T){ for(ThreadNode *p = Firstnode(T);p!=NULL;p=Nextnode(p)) visit(p); }
3 树、森林
3.1 树的存储结构
-
双亲表示法
#define MAX_TREE_SIZE 100 //树中最多结点数 typedef struct{ //树的结点定义 ElemType data;//数据元素 int parent;//双亲位置域 }PNode; typedef struct{ //树的类型定义 PNode node[MAX_TREE_SIZE]; //双亲表示 int n; //结点数 }PTree; -
孩子兄弟表示法
typedef struct CSnode{ ElemType data; //数据域 struct CSNode *firstchild,*nextsibling;//第一个孩子和右兄弟指针 }CSNode,*CSTree;
3.2 树的先根遍历
伪代码
void PreOrder(TreeNode *R){
if(R!=NULL){
visit(R); //访问根节点
while(R还有下一个子树T)
PreOrder(T); //先根遍历下一颗子树
}
}
4 树的应用
4.1 二叉排序树BST
4.1.1 二叉排序树递归查找
//在二叉排序树中查找值为key的结点
BSTNode *BST_Search(BSTree T,int key){
while(T!=NULL&&key!=T->ley){ //若树空或等于根节点值,则结束循环
if(key < T->key)
T = T->lchild; //小于,则在左子树上查找
else
T = T->rchild; //大于,则在右子树上查找
}
return T;
}
//在二叉排序树中查找值为key的结点,递归实现
BSTNode *BSTSearch(BiTree T,int key){
if(T!=NULL)
return NULL; //查找失败
if(key==T->key)
return T; //查找成功
else if(key < T->key)
return BSTSearch(T->lchild,key); //在左子树中找
else
return BSTSearch(T->rchild,key); //在右子树中找
}
4.1.2 二叉排序树非递归查找
BSTNode *BST_Search(BiTree T,ElemType key,BiTNode *&p){
//查找函数返回指向关键字值为key的结点指针,若不存在返回NULL
p = NULL;//p指向被查找结点的双亲结点,用于插入删除操作
while (T != NULL && key != T->data) {
p = T;
if (key < T->data)
T= T->lchild;
else
T=T->rchild;
}
return T;
}
4.1.3 二叉排序树插入
int BST_Insert(BiTree &T,KeyType k){
//在二叉排序树T中插入一个关键字为k的结点
if(T==NULL){
//原树为空,新插入的记录为根结点
T=(BiTree)malloc(sizeof(BSTNode));
T->key = k ;
T->lchild = T->rchild = NULL;
return 1; //返回1,表示成功
}
else if(k==T->key) //树中存在相同关键字的结点
return 0;
else if(k < T->key) //插入到T的左子树中
return BST_Insert (T->lchild,k);
else //插入到T的右子树中
return BST_Insert (T->rchild,k);
}
4.1.4 二叉排序树构造
void Creat_BST(BiTree &T,KeyType str[],int n){//用关键字数组str[]建立一个二叉排序树
T = NULL; //初始时bt为空树
int i = 0;
while (i < n){//依次将每个元素插入
BST_Insert(T, str[i]);
i++;
}
}
4.2 平衡二叉树AVL
4.2.1 平衡二叉树的存储结构
typedef struct AVLNode{
int key; //数据域
int blance; //平衡因子
struct AVLNode *lchild,*rchild;
}AVLNode,*AVLTree;