JZ2 替换空格
(简单)
题目
描述
请实现一个函数,将一个字符串中的每个空格替换成“%20”。例如,当字符串为We Are Happy.则经过替换之后的字符串为We%20Are%20Happy。
示例
输入:
“We Are Happy”
返回值:
“We%20Are%20Happy”
思路
用 Java 实现的话,便可借用 String 类的内置方法 replaceAll(String regex, String replacement),当然,此题也可自己实现这个函数的类似功能,例如将字符串对象转为字符数组,之后遍历数组的同时替换空格字符。如果是用 C 语言的话,那么需用指针进行遍历处理,但也没什么难点,因此我觉得此题出的也没什么意思。
实现
public class JZ2替换空格 {
public String replaceSpace (String s) {
if (s == null || s.length() == 0) {
return s;
}
String str = s.replaceAll(" ", "%20");
return str;
}
}

JZ1 二维数组中的查找
(简单)
题目
描述
在一个二维数组中(每个一维数组的长度相同),每一行都按照从左到右递增的顺序排序,每一列都按照从上到下递增的顺序排序。请完成一个函数,输入这样的一个二维数组和一个整数,判断数组中是否含有该整数。
[
[1,2,8,9],
[2,4,9,12],
[4,7,10,13],
[6,8,11,15]
]
给定 target = 7,返回 true。
给定 target = 3,返回 false。
示例
输入:
7,[[1,2,8,9],[2,4,9,12],[4,7,10,13],[6,8,11,15]]
返回值:
true
说明:
存在7,返回true
思路
由于本人对于一维数组的二分查找比较熟悉,因此看到此题,我当时想到了三种方法。
1 完全暴力:直接两个循环来进行查找,此方法比较无脑,不再进行实现。
2 半暴力 + 二分查找:可以一个循环来遍历行,而在此循环内,进行本行中目标值的二分查找,时间复杂度为 O(nlogn) 实现如下:
【实现】
public class JZ1二维数组中的查找 {
public boolean Find(int target, int[][] array) {
int rowCount = array.length;
int colCount = array[0].length;
for (int i = 0; i < array.length; i++) {
if (binarySearch(array[i], target)) {
return true;
}
}
return false;
}
public boolean binarySearch(int[] array, int target) {
if (array == null || array.length == 0) {
return false;
}
int start = 0;
int end = array.length - 1;
int mid = 0;
while (start <= end) {
mid = (start + end) / 2;
if (target < array[mid]) {
end = mid - 1;
} else if (target > array[mid]) {
start = mid + 1;
} else {
return true;
}
}
return false;
}
}

3 直接二分查找:此方法是行不通的,虽然行的首元素从左到右递增,列的首元素从上到下递增,但由于一行数据的最后一个元素可能大于下一行的第一个元素或者最后一个元素,因此,我们无法通过将一维的二分查找直接改为二维的二分查找来实现。
(在我后来看题解复盘时,有位大佬的图解很形象地解释出了我上面那段话的意思,见下图)
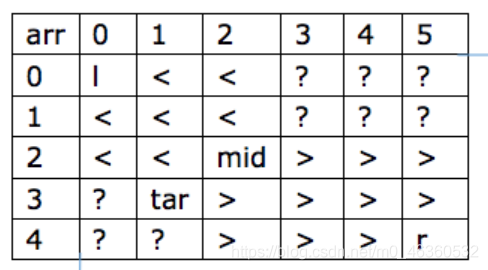
下面是我当初的错误示范,不出意料,提交报错。
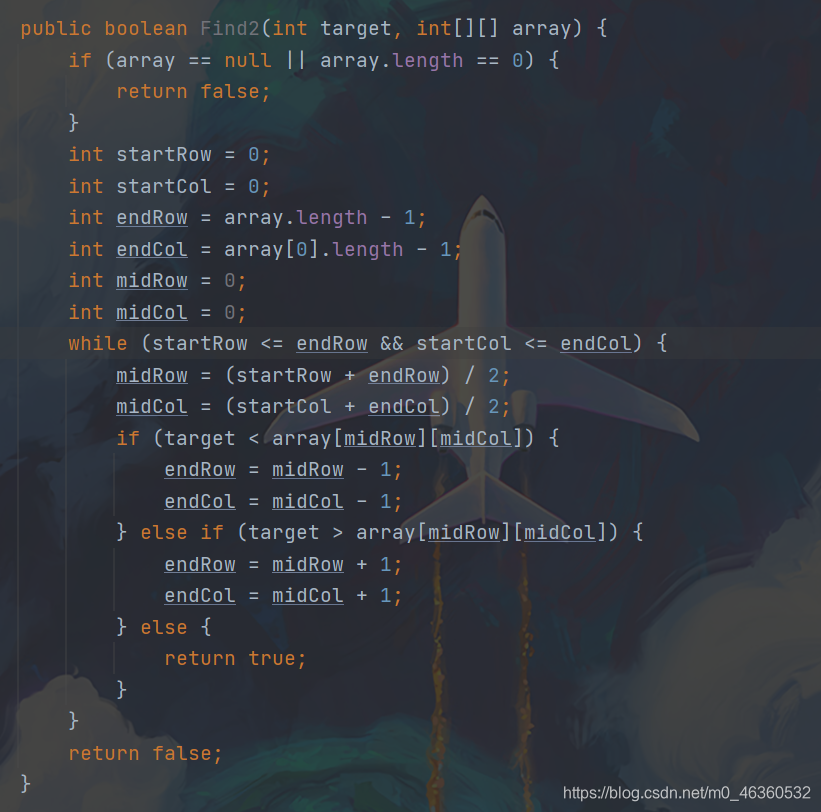
4 一种巧妙方法:(这里参考的是此位大佬的思路:https://blog.nowcoder.net/n/f146364d1331407080adbbb5a062e067?f=comment,虽然这个思路十分容易理解,但我当时做题时由于一直考虑怎么用二分查找来解决问题,导致忽略了这一种想法,十分不应该。
具体思路:如果我们把二分值定在右上角或者左下角,就可以进行二分。这里以右上角为例,左下角可自行分析
时间复杂度:O(m+n) ,其中m为行数,n为列数,最坏情况下,需要遍历m+n次。
空间复杂度:O(1)。
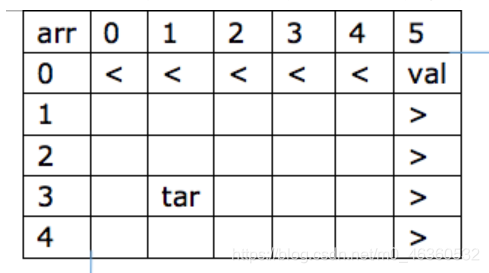
【实现】
public class Solution {
public boolean Find(int target, int [][] array) {
if (array == null || array.length == 0) {
return false;
}
int rowCount = array.length;
int colCount = array[0].length;
//初始参考右上角元素
int rowFlag = 0;
int colFlag = colCount - 1;
while (rowFlag < rowCount && colFlag >= 0) {
if (target == array[rowFlag][colFlag]) {
return true;
} else if (target > array[rowFlag][colFlag]) {
rowFlag++;
} else {
colFlag--;
}
}
return false;
}
}

