5.1 树和二叉树的定义
5.1.0 回顾线性结构和非线性结构的区别

线性结构:前驱与后继1对1。
非线性结构:前驱与后继1对n,或者m对n。
5.1.1 树的定义

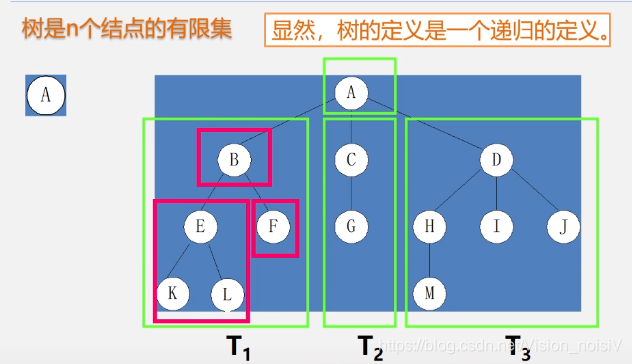
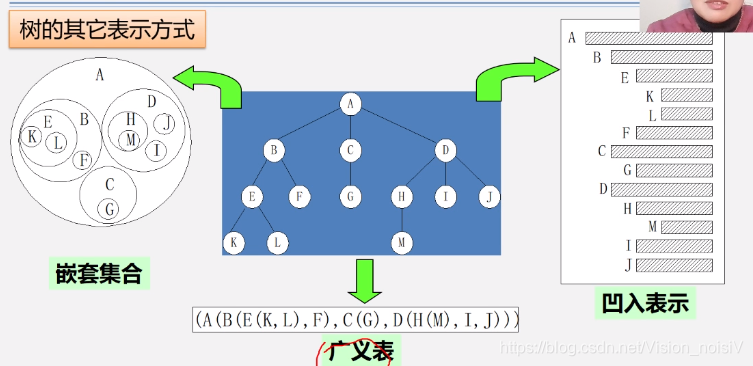
注意:树的结构定义就是递归的
5.1.2 树的基本术语
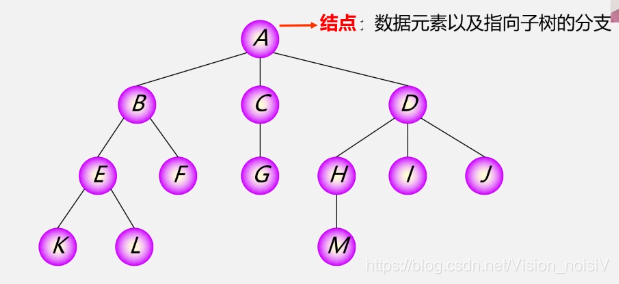
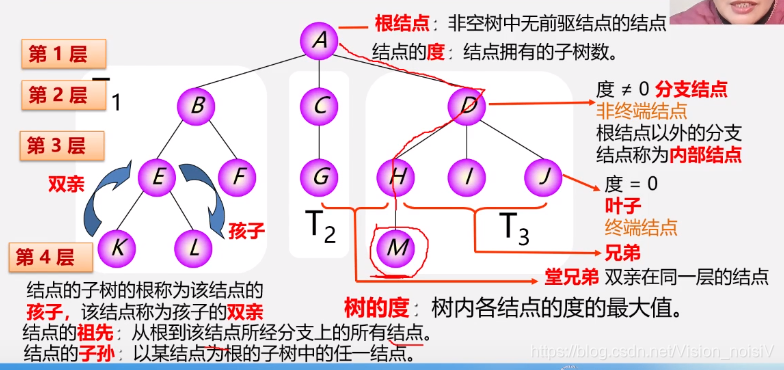
树的深度:树中结点的最大层次。
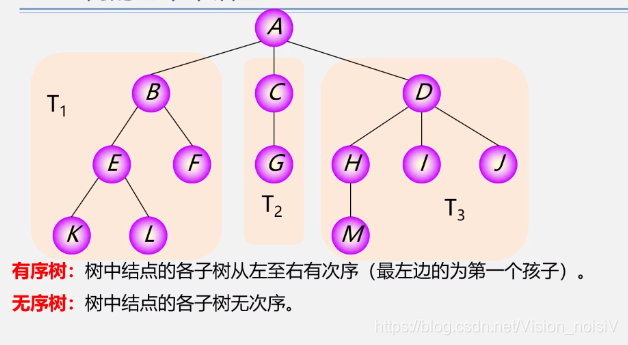

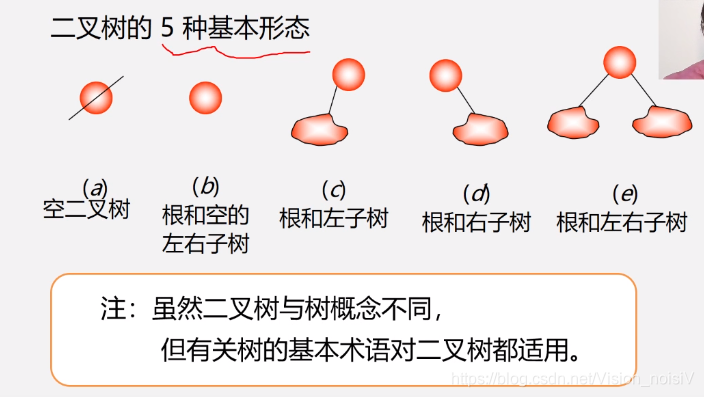
5.1.3 二叉树的定义


二叉树不是树的特殊情况:

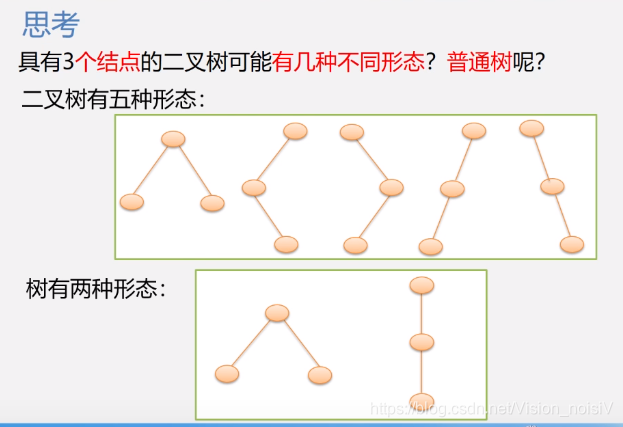
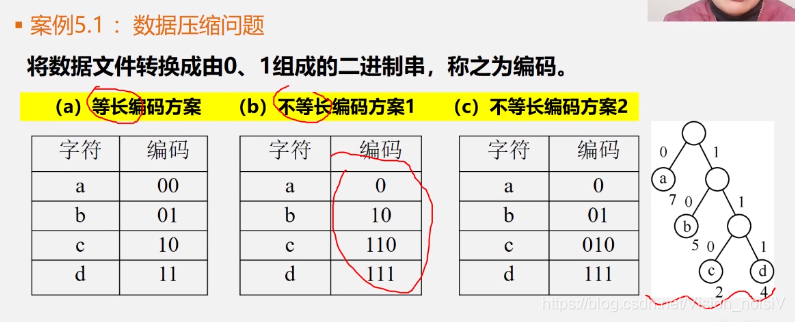
5.2 案例引入

5.3 二叉树的抽象数据类型定义


5.4 二叉树的性质
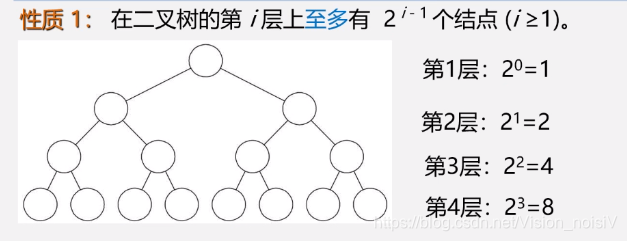
5.4.1 性质1
在二叉树的第i层最多有多少结点?

5.4.2 性质2
二叉树最多有多少结点?


5.4.3 性质3
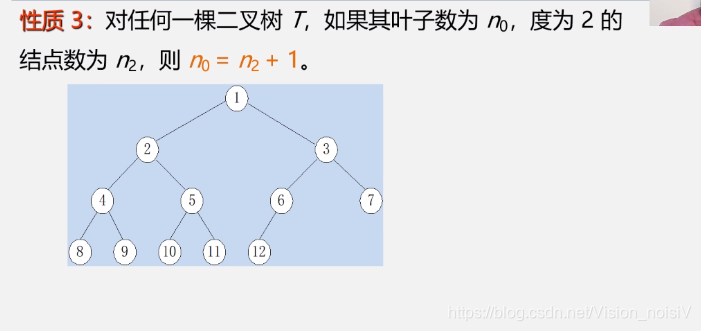
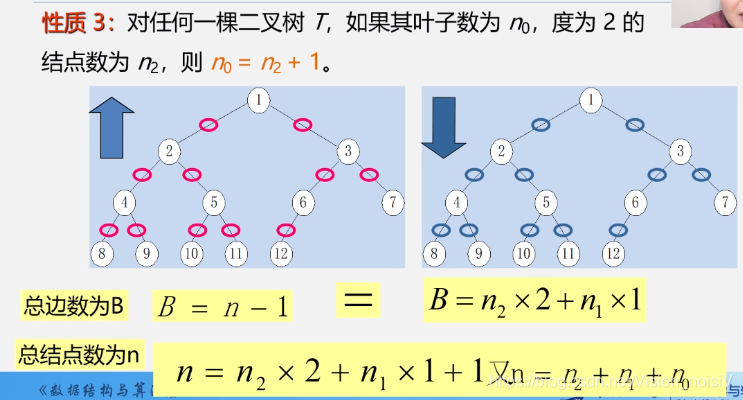
性质3的结论并不是很重要,重要的是推出这个结论的过程:
从下往上看,是一个节点对应一条边,但是根节点不对应边,也就是总边树B=n-1;
而从上往下看,是一个度为2的结点对应2个边,度为1的结点对应1个边,度为0的结点对应0个边,也就是总边树B=n22+n11。
而总边数又是一致的,因此得到性质3。
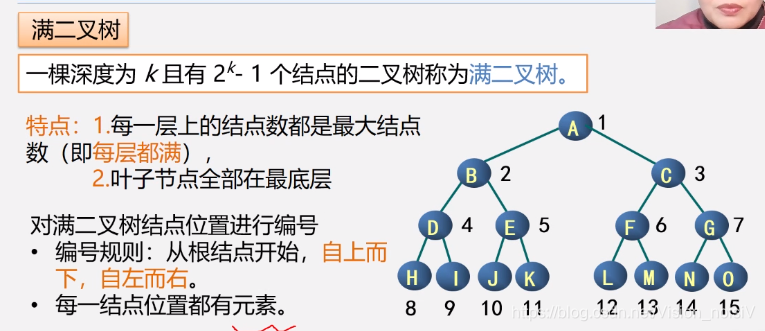
5.4.4 满二叉树
满二叉树和完全二叉树,它们在顺序存储方式下可以复原,这也是为什么研究它们的原因。
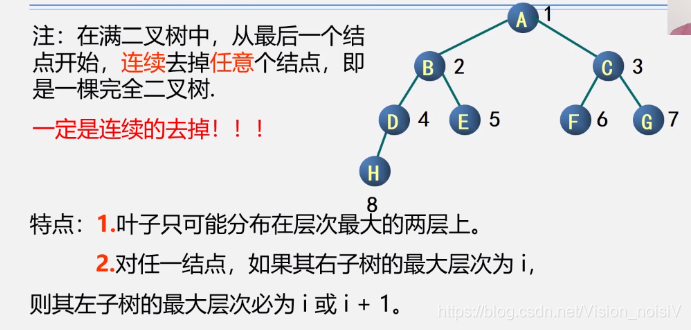
5.4.5 完全二叉树
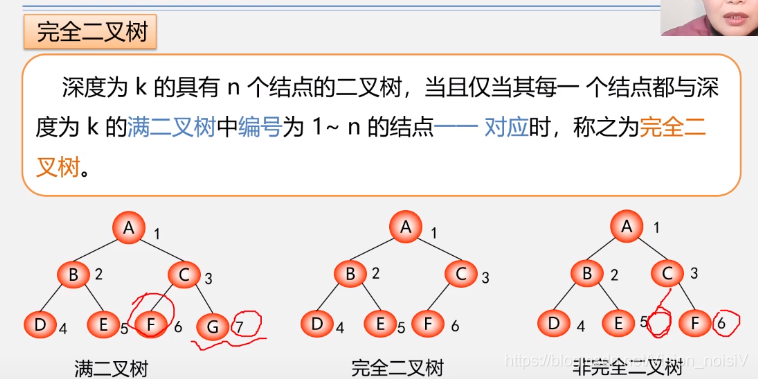
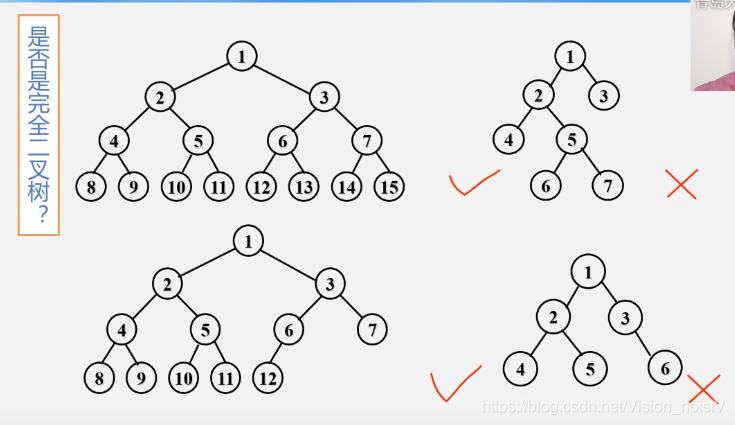
完全二叉树判断的简便方法:
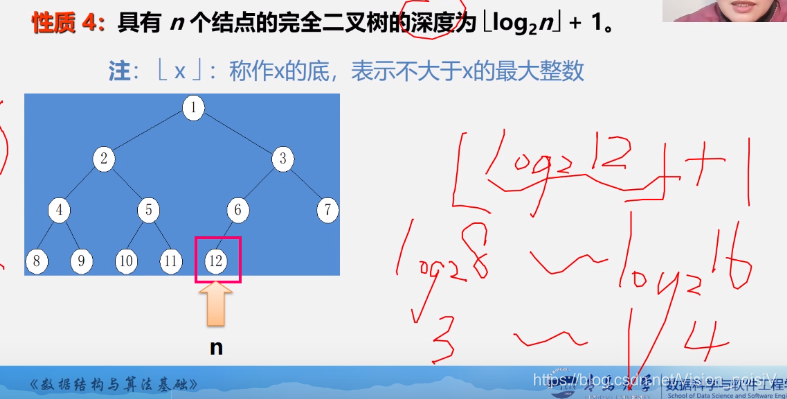
5.4.5.1 性质4:完全二叉树的结点个数和树深度的关系
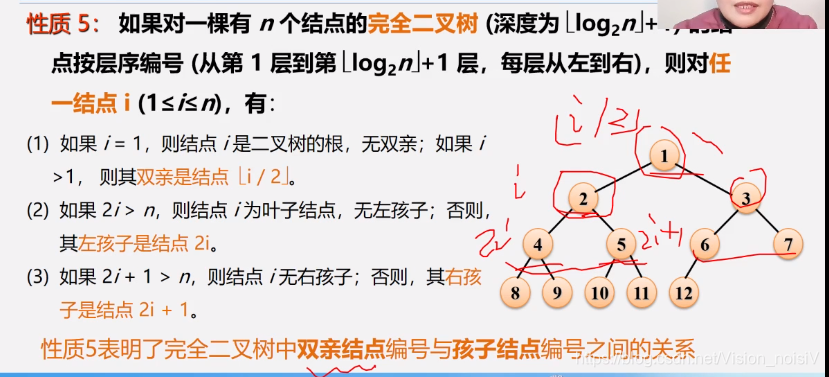
5.4.5.1 性质5:完全二叉树的双亲和孩子编号的关系
5.5 二叉树的存储结构
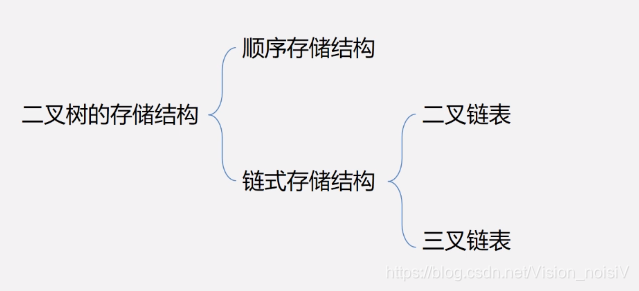
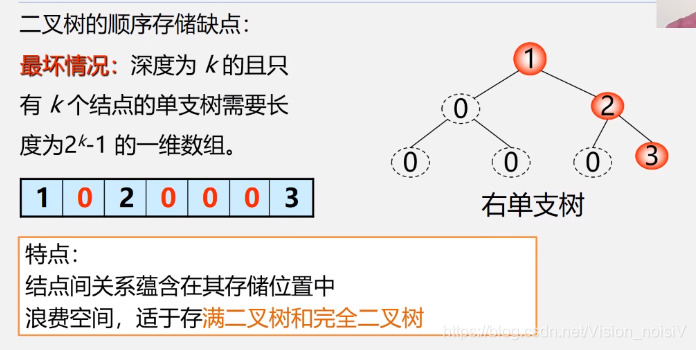
5.5.1 二叉树的顺序存储结构
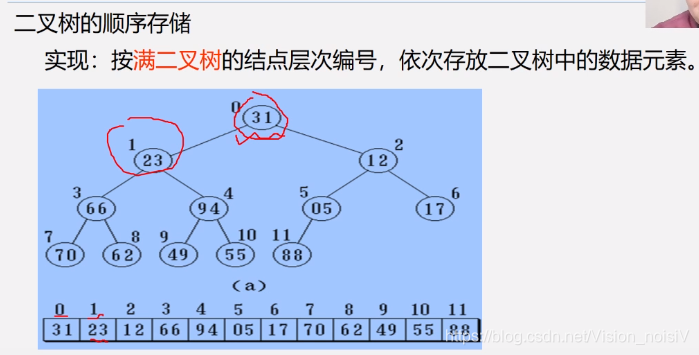
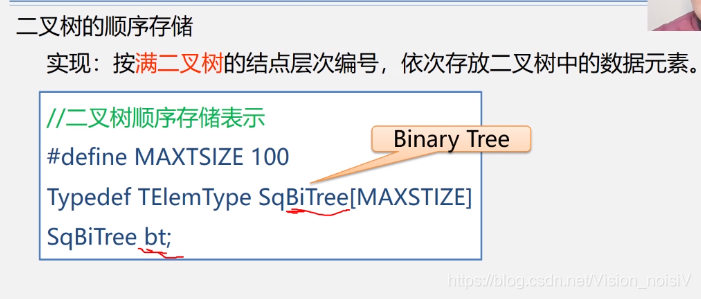
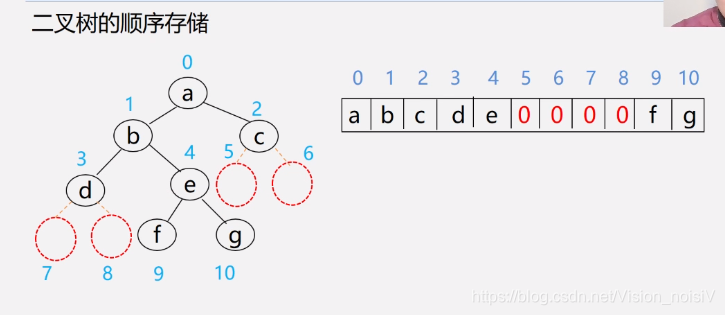
采用以上存储的方式,能够做到从存储结构恢复到树原来的结构。
5.5.2 顺序存储的特点
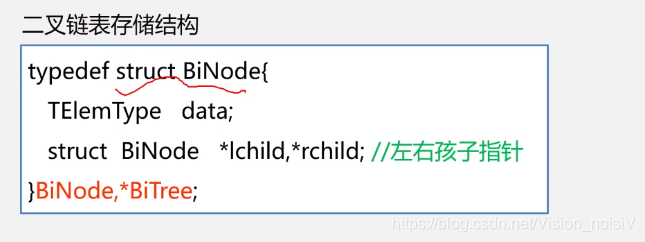
5.5.3 二叉树的链式存储结构

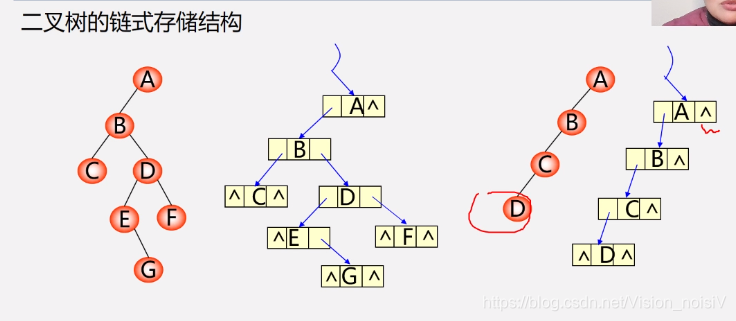
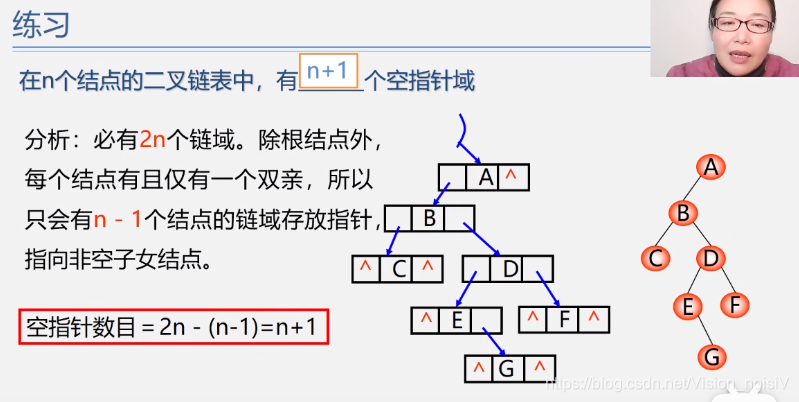
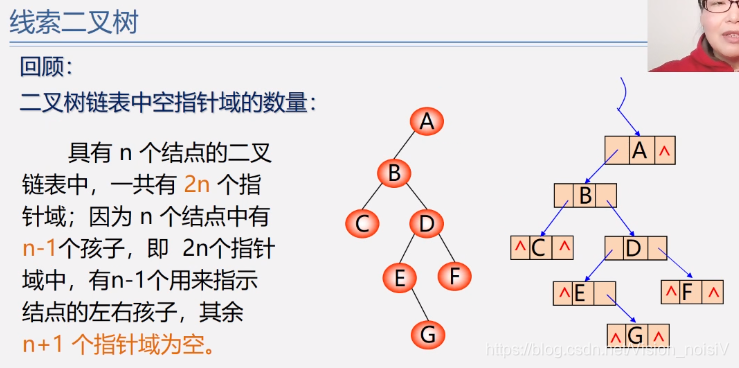
分析:n个结点必有2n个链域这是肯定的。当从下往上看时,一个结点必对应一个链域存放指针,除了根节点,那么就是有n-1个结点的链域存放指针。
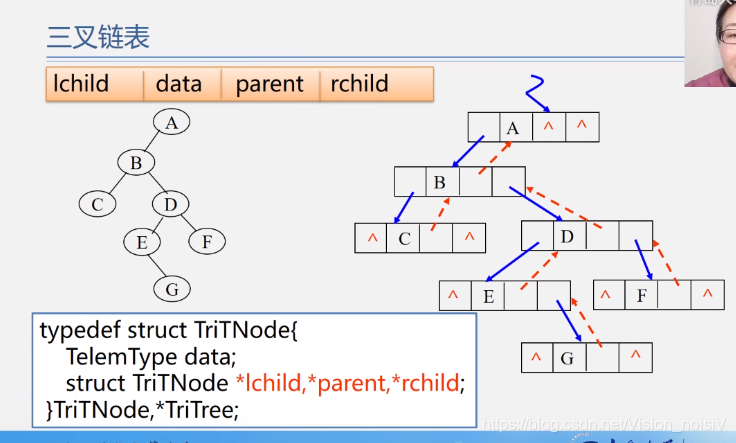
5.6 二叉树的遍历
注意:以下算法要反复理解,反复编写,吃透!
5.6.1 遍历的定义



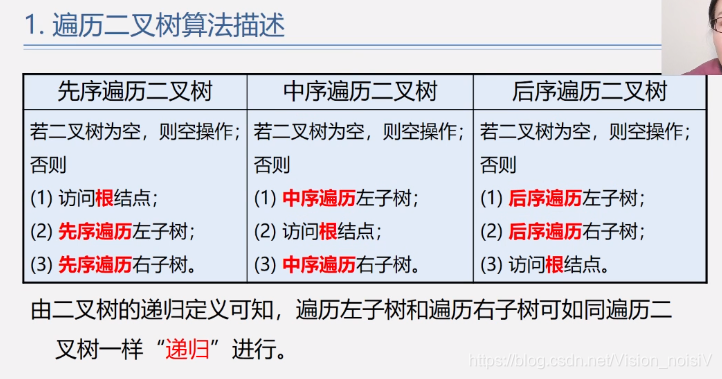
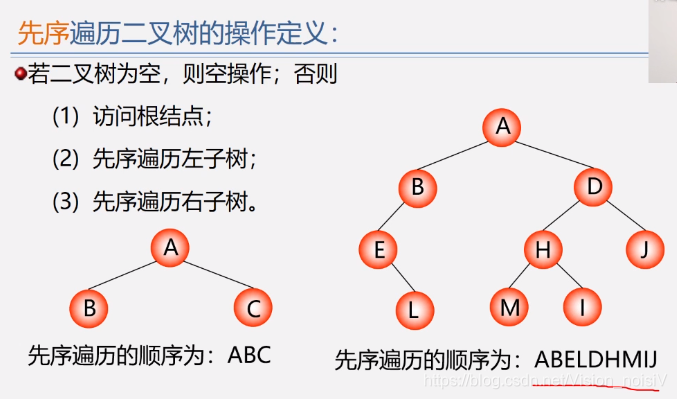
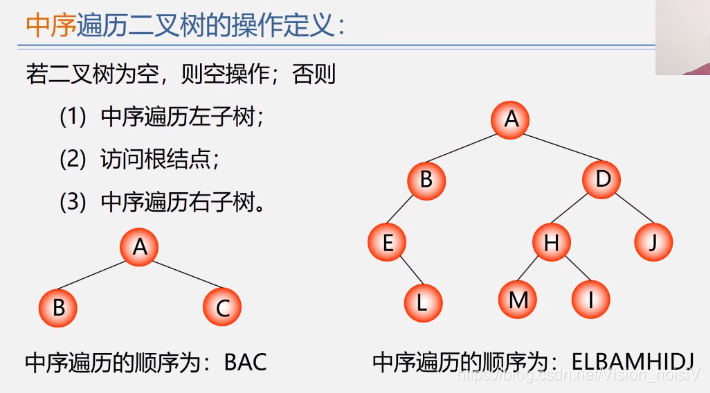
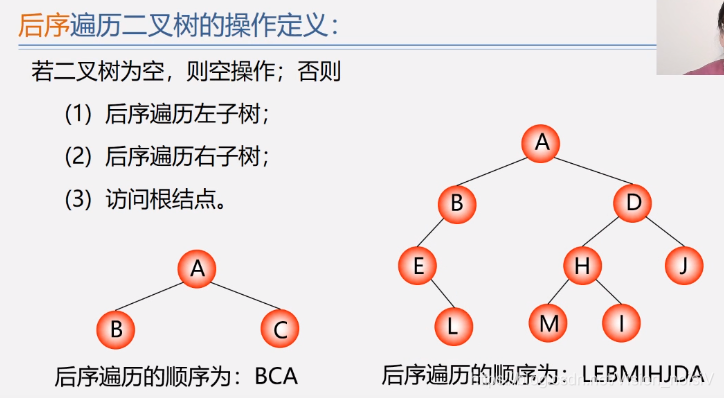
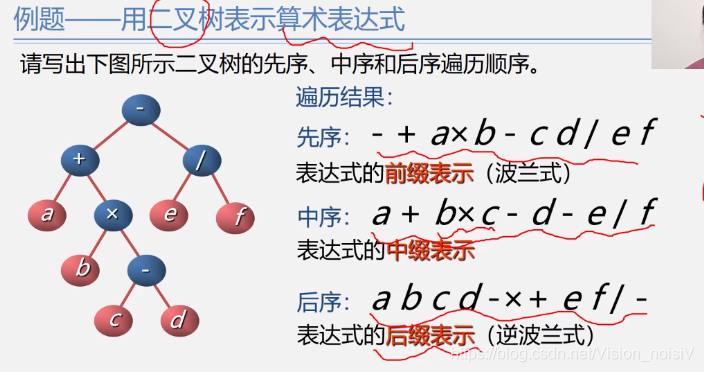
注意:可以用以上方式进行中缀表达式和后缀表达式(逆波兰表达式)之间的转换。
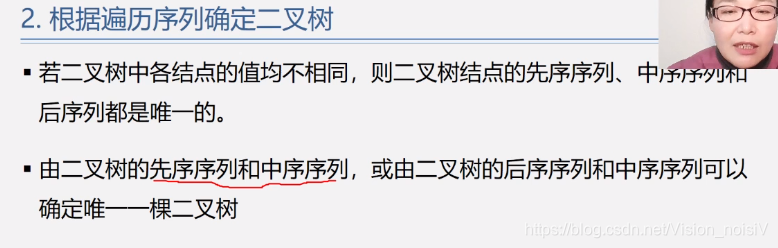
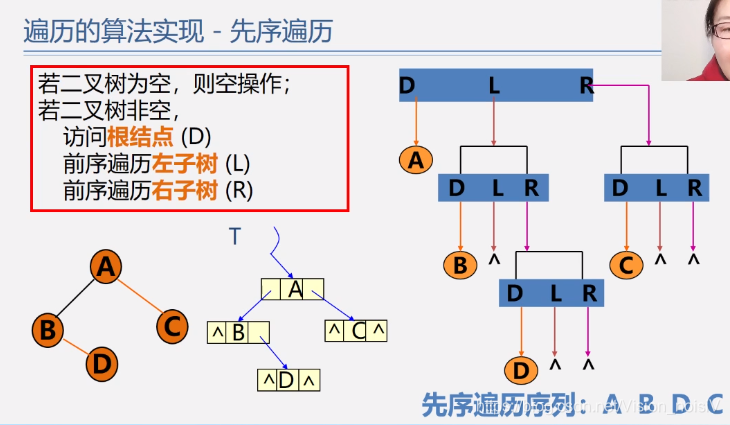
5.6.2 先序遍历算法——二叉链表

typedef int Elemtype;
typedef struct BiNode {
Elemtype data;
BiNode* lchild, * rchild;
}BiNode, * Bitree;
void ShowBT(Bitree BT) {//先序遍历_递归实现
if (BT == NULL) return;
else {
cout << BT->data;
ShowBT(BT->lchild);
ShowBT(BT->rchild);
}
}
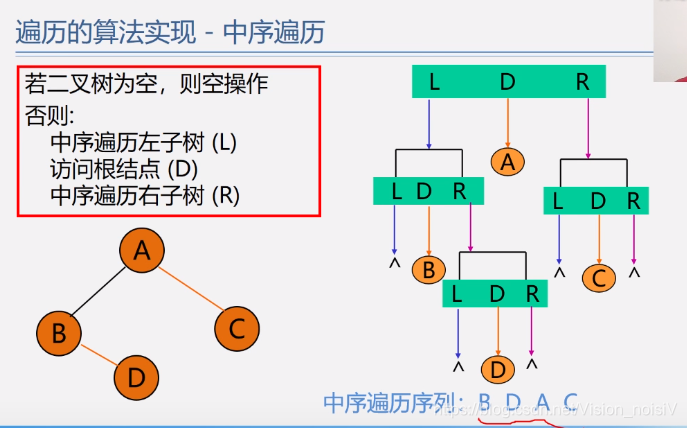
5.6.3 中序遍历算法——二叉链表

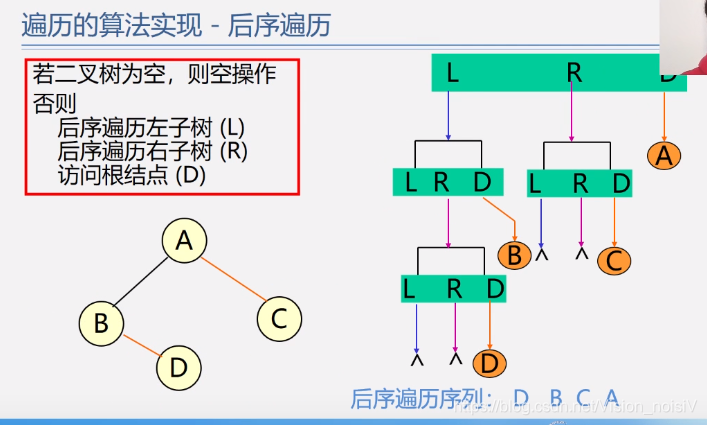
5.6.4 后序遍历算法——二叉链表

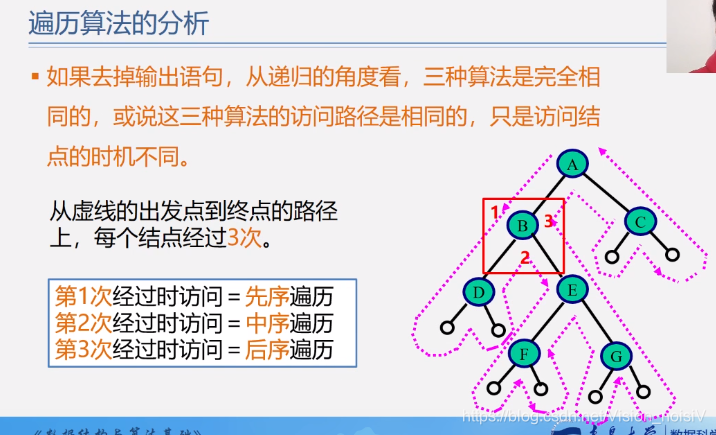
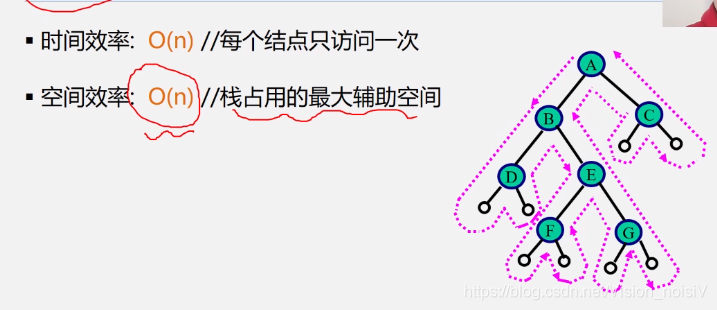
5.6.5 非递归算法实现中序遍历

如果不懂,再看一下老师的ppt的动画。
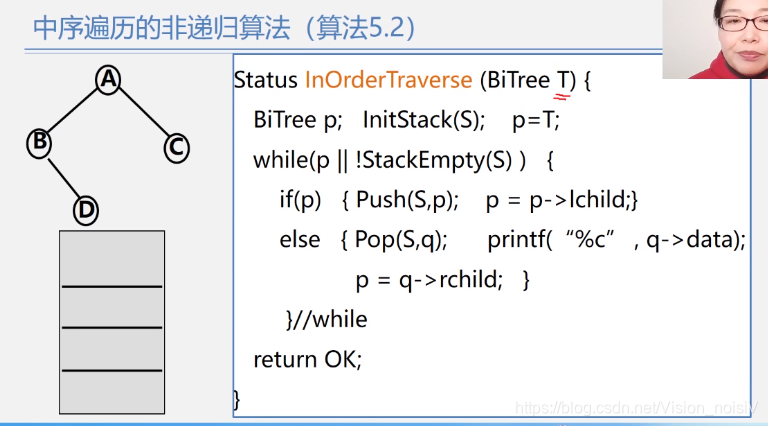
typedef int Elemtype;
typedef struct BiNode {
Elemtype data;
BiNode* lchild, * rchild;
}BiNode, * Bitree;
#define Maxsize 10//注意后面没有分号;
typedef Bitree SElemtype;//将指向树的结点的指针作为栈的元素
typedef struct {
SElemtype* base;
SElemtype* top;
int stacksize;
}SqStack;
int InitStack(SqStack& S) {
S.base = new SElemtype[Maxsize];
if (!S.base) return -2;
S.top = S.base;
S.stacksize = Maxsize;
return 1;
}
int PUSH(SqStack& S, SElemtype e) {
if (S.top - S.base == S.stacksize) return -2;
*S.top++ = e;
return 1;
}
int POP(SqStack& S, SElemtype& e) {
if (S.top == S.base) return -2;
e = *--S.top;
return 1;
}
bool isEmptyS(SqStack S) {
if (S.base) {//如果栈存在
if (S.base == S.top) return true;
}
return false;
}
void ShowBT_Iteration(Bitree BT) {//用迭代实现中序遍历
Bitree p = BT;//创建一个指针,指向二叉树的根
SqStack Stack;
InitStack(Stack);
while (p || !isEmptyS(Stack)) {
if (p) {
PUSH(Stack, p);
p = p->lchild;
}
else {
POP(Stack, p);
cout << p->data;
p = p->rchild;
}
}
}
5.6.6 层序遍历
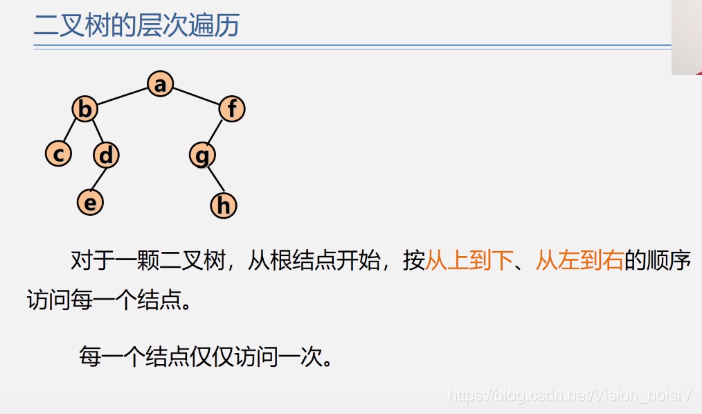

如果看不懂,看老师ppt。
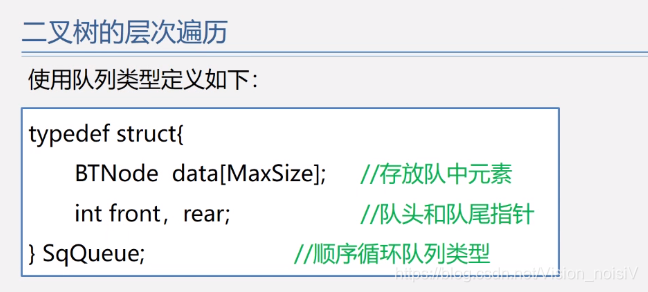
front:指向对头元素;
rear:指向队尾元素的下一个元素,少用一个元素空间。

5.6.7 二叉树的建立
以先序遍历为例:
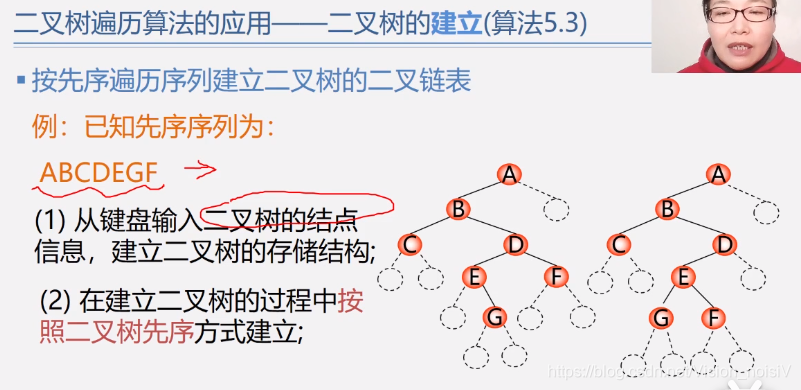

typedef int Elemtype;
typedef struct BiNode {
Elemtype data;
BiNode* lchild, * rchild;
}BiNode, * Bitree;
void CreatBT(Bitree& BT) {//利用先序遍历来创建二叉树_递归实现
int input;
cin >> input;//输入数字0表示该分支创建结束。
if (input == 0) {
BT = NULL;
}
else {
BT = new BiNode;
BT->data = input;
CreatBT(BT->lchild);
CreatBT(BT->rchild);
}
}
5.6.8 复制二叉树
采用的是先序遍历

5.6.9 计算二叉树的深度

5.6.10 求二叉树结点的个数
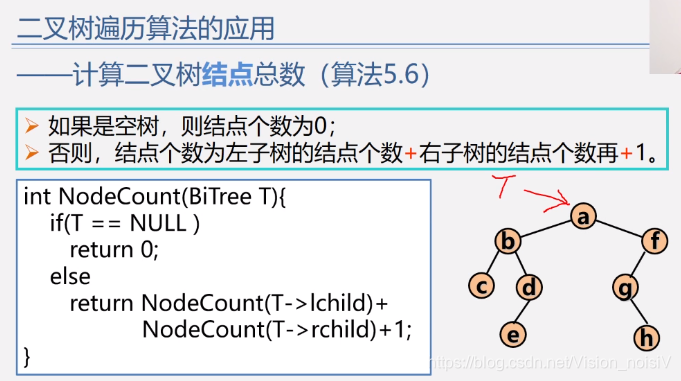
5.6.11 求二叉树的叶子结点数
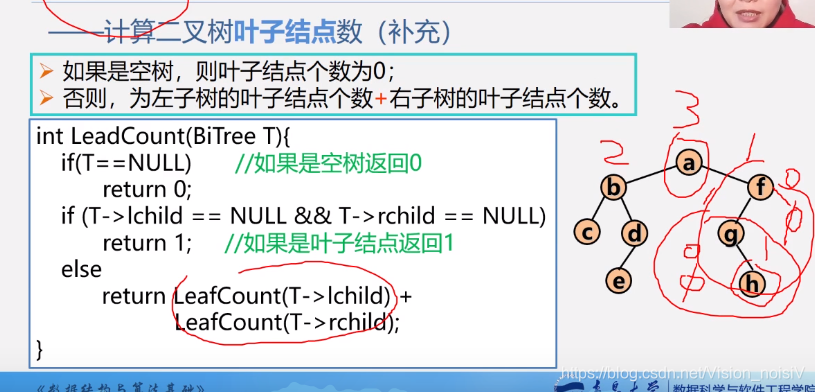
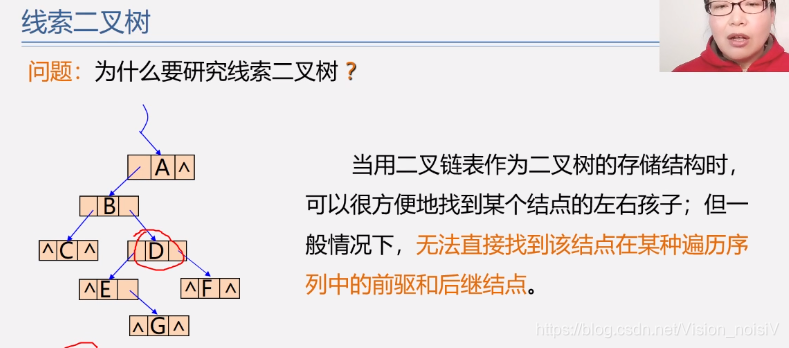
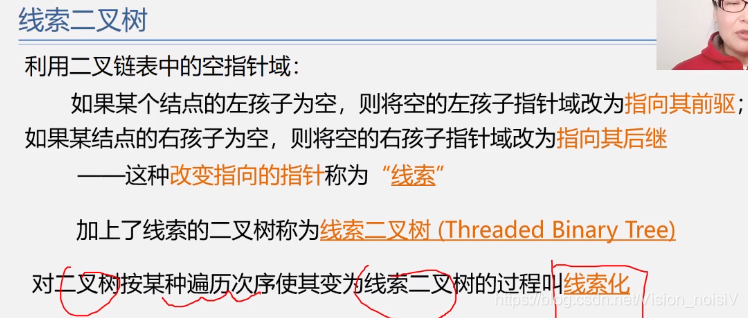
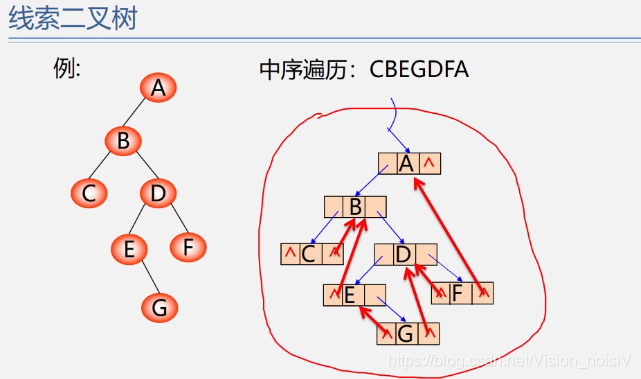
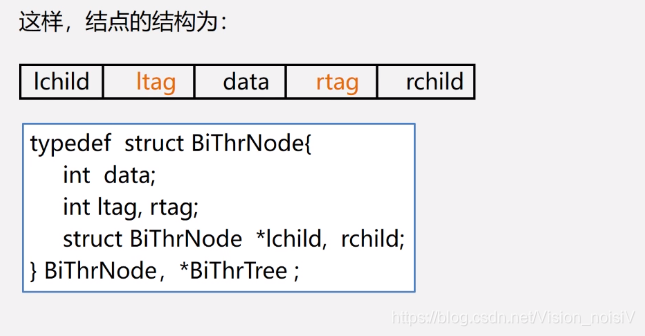
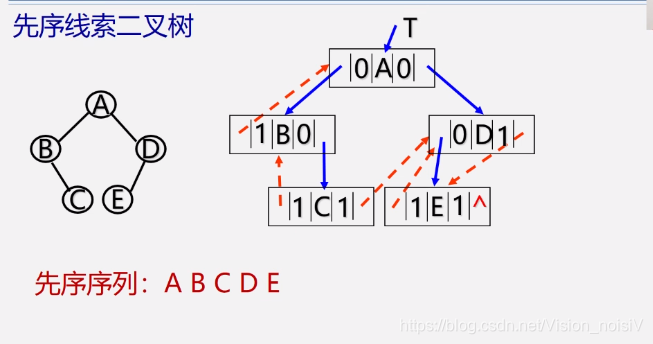
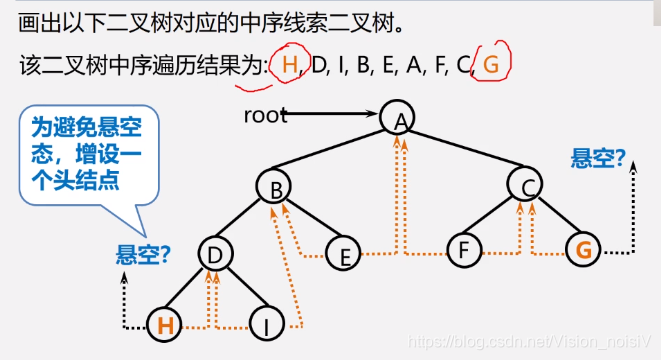
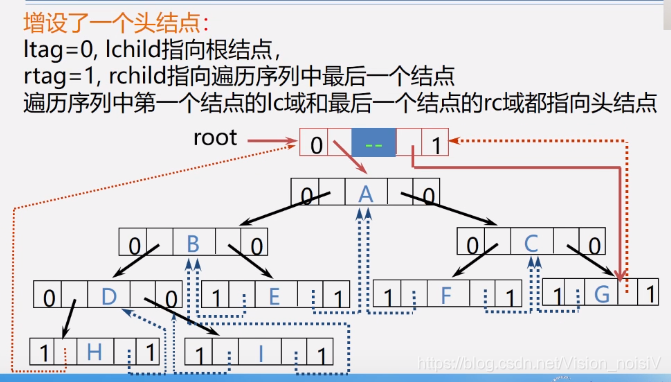
5.6.12 线索二叉树

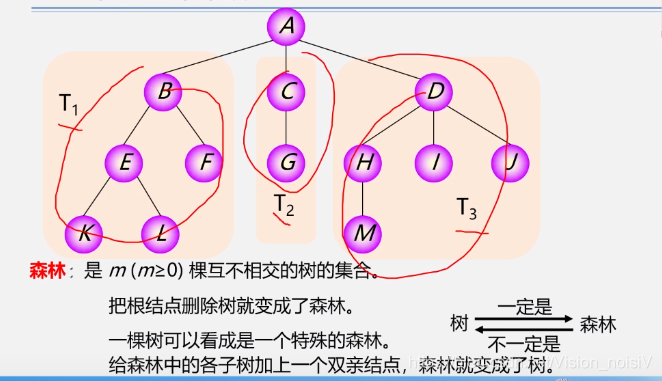
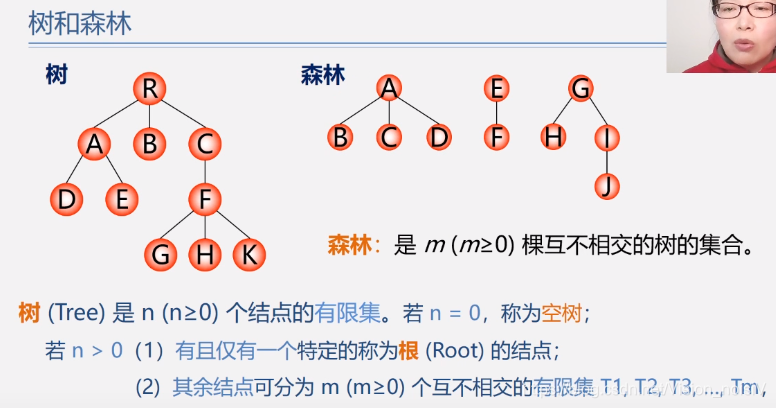
5.7 树和森林

5.7.1 树的存储结构
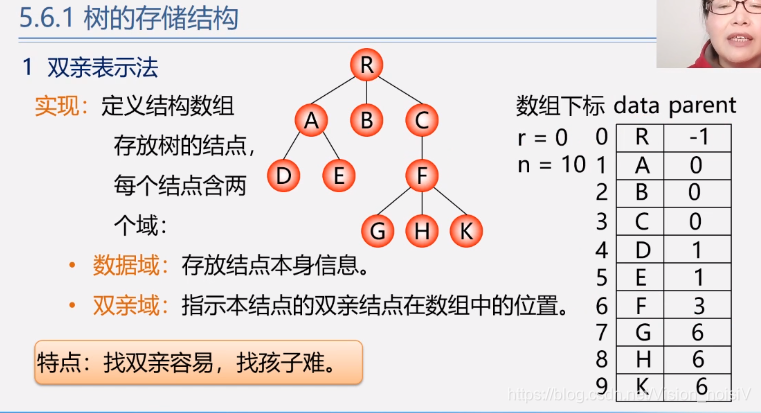



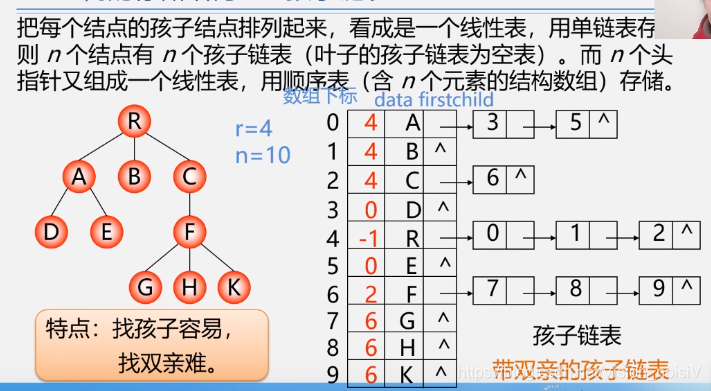

特点:以上表示容易找孩子和兄弟,不易找双亲。
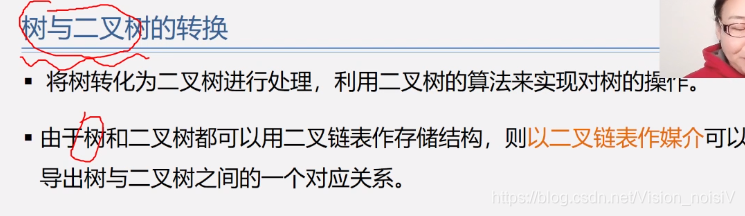
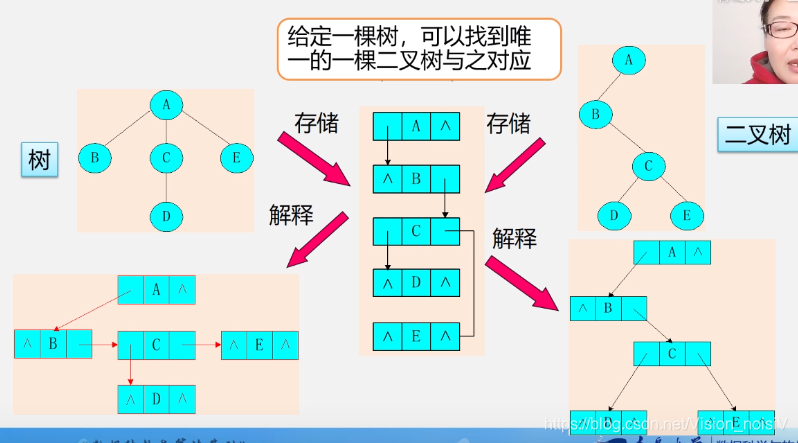
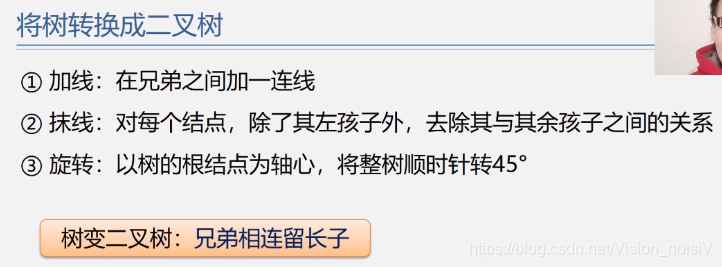
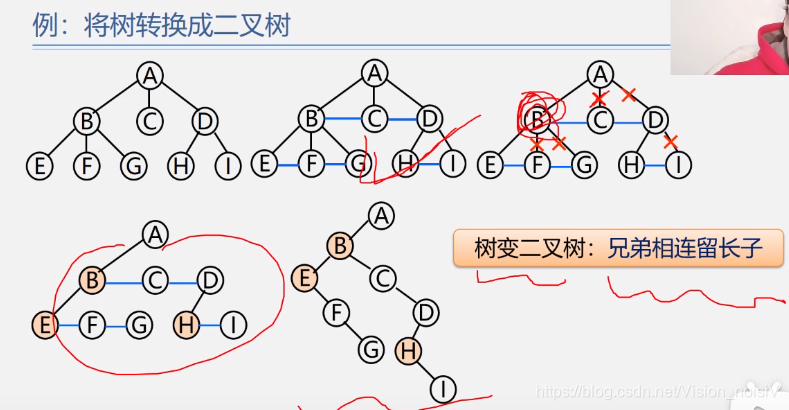
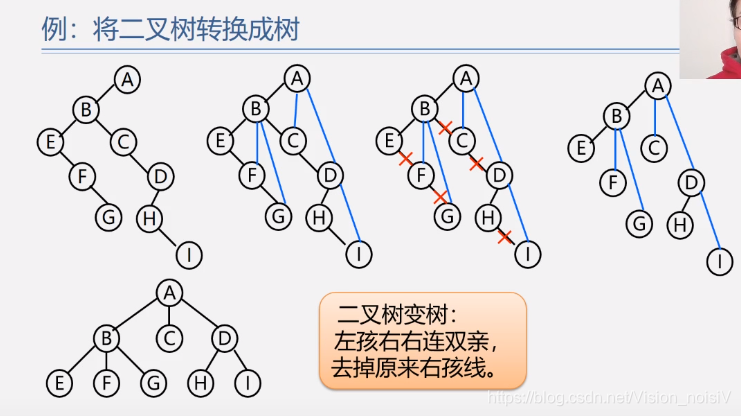
5.7.2 树和二叉树的转换
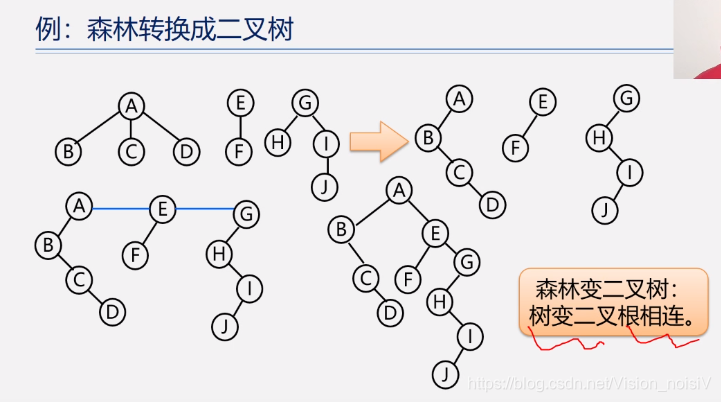
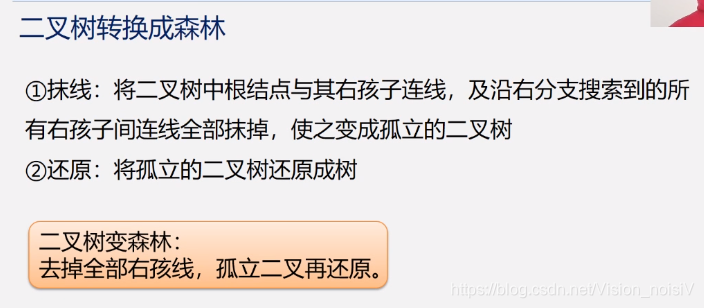
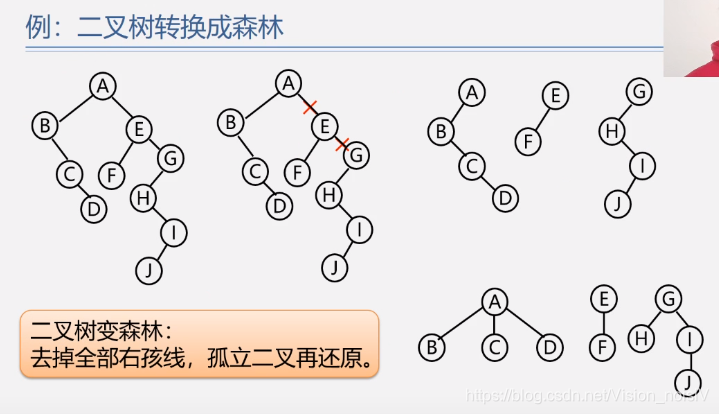
5.7.3 森林和二叉树的转换

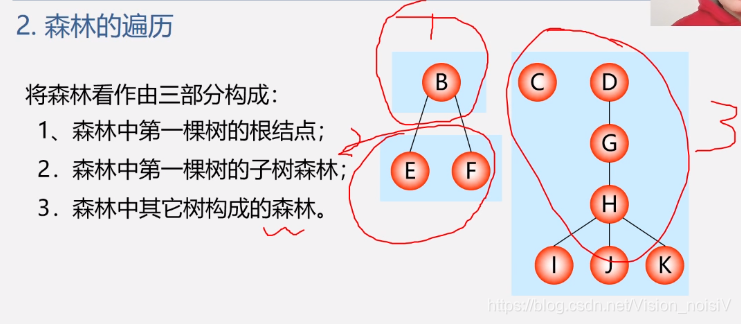
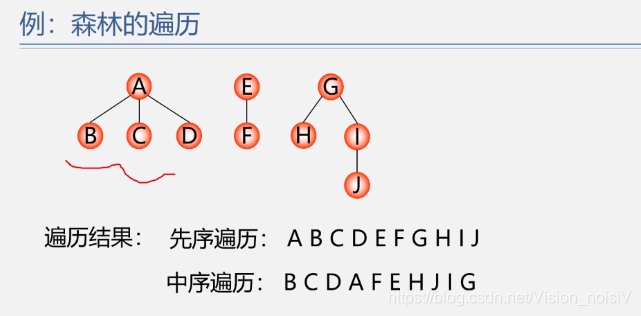
5.7.4 树和森林的遍历
由于树的每个结点可能有多个孩子,所以没有“中序遍历”。



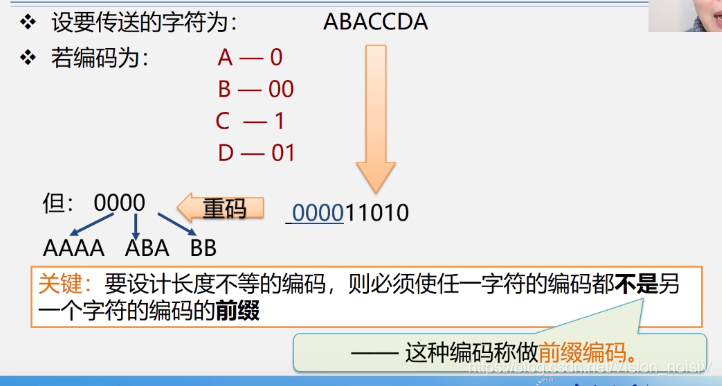
5.8 哈夫曼树及其应用
5.8.1 基本概念

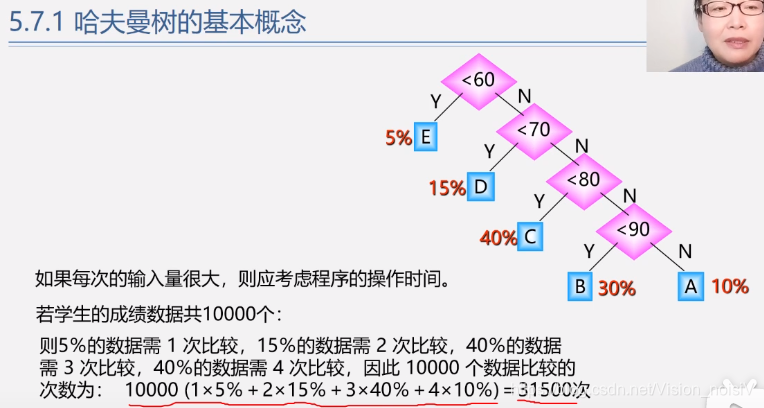
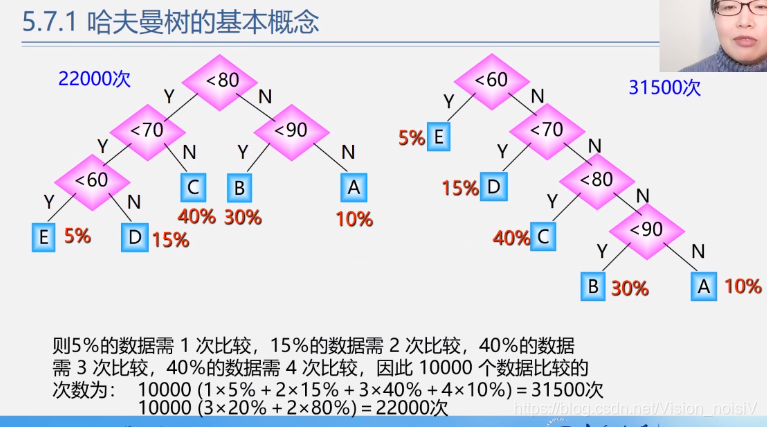
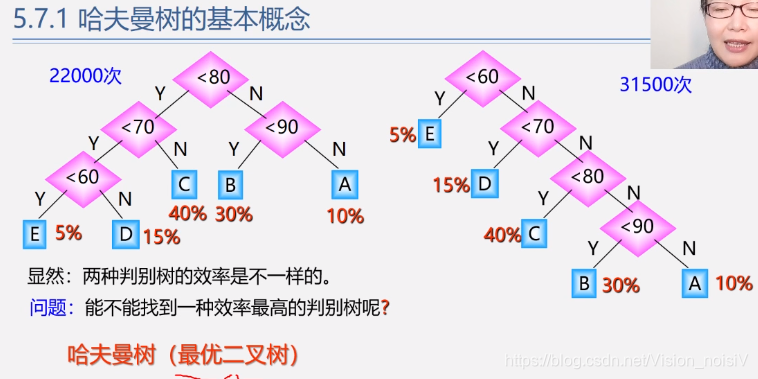
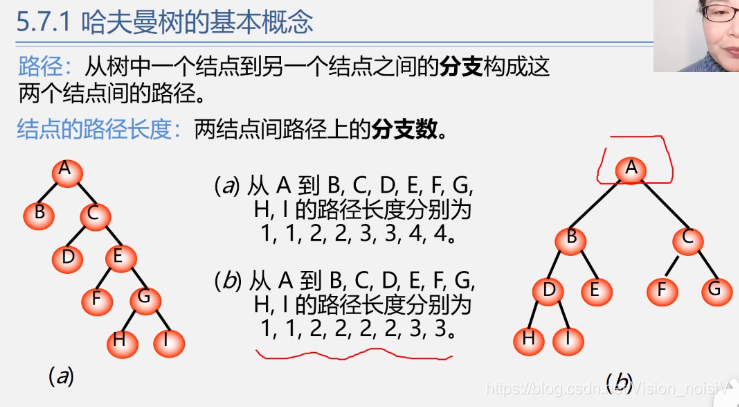
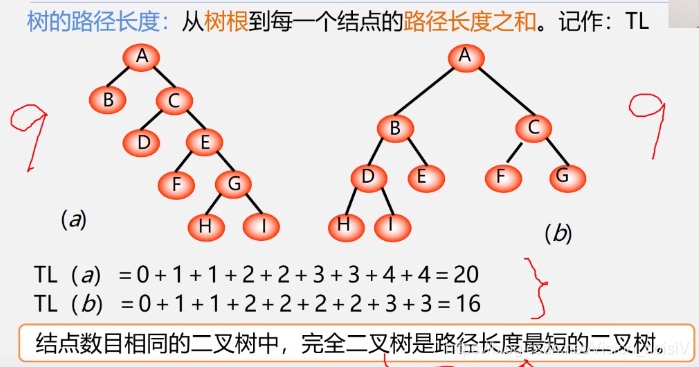
反之不一定,树的路径最短的不一定是完全二叉树。

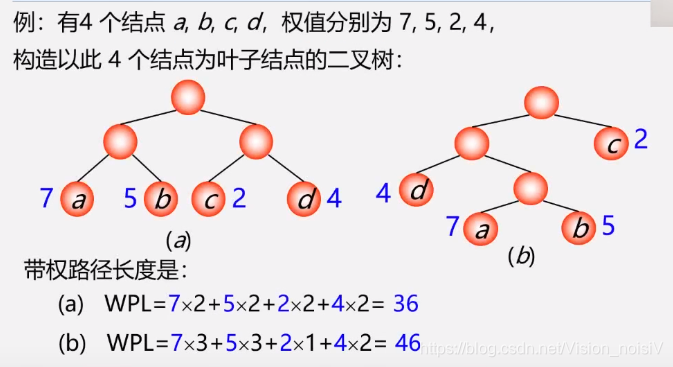

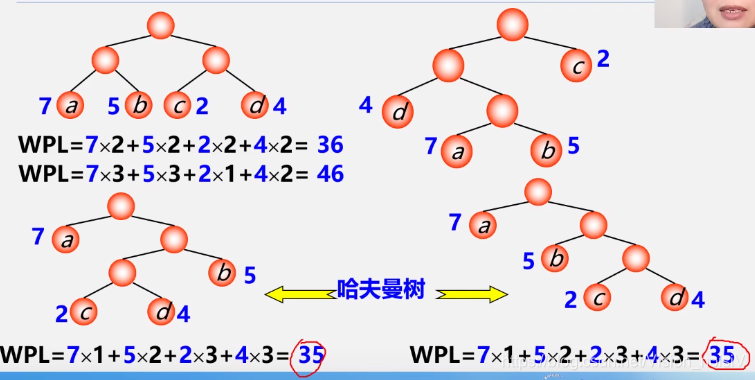
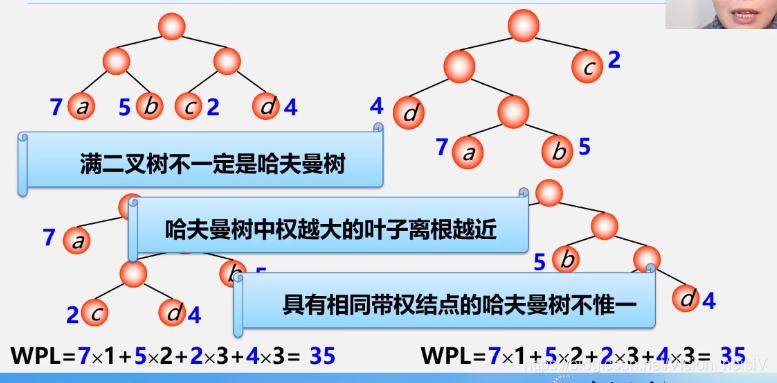
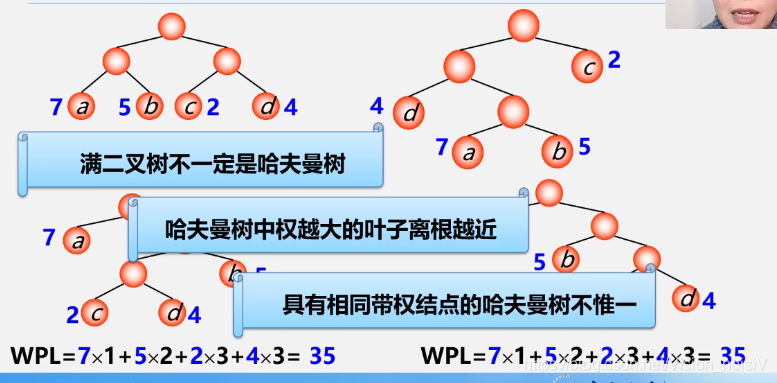
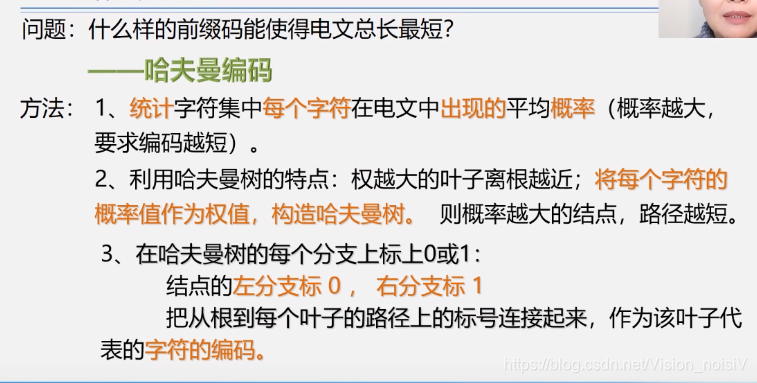
5.8.2 构造哈夫曼树方法
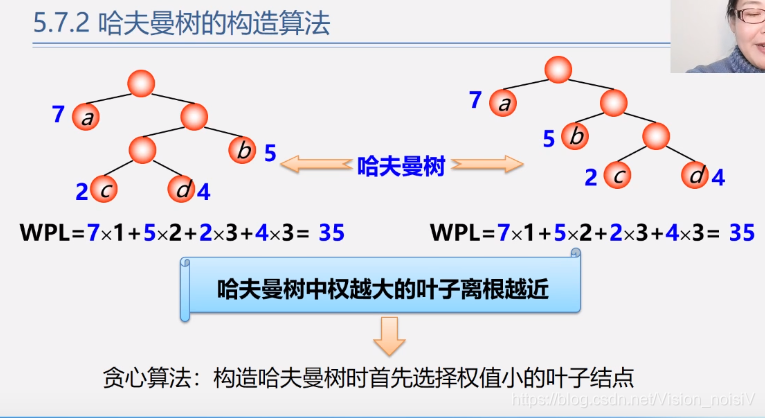

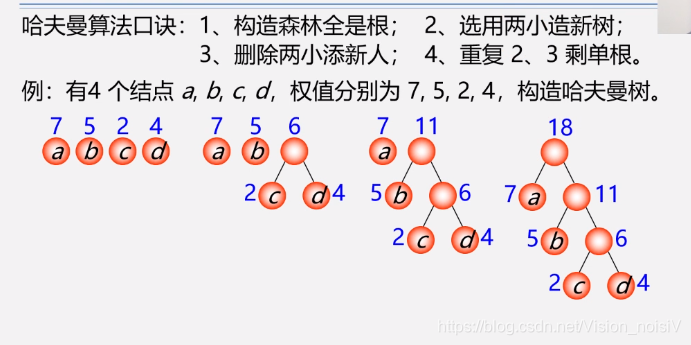
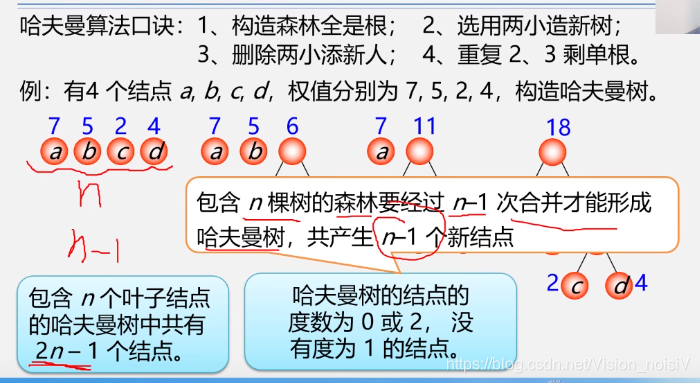
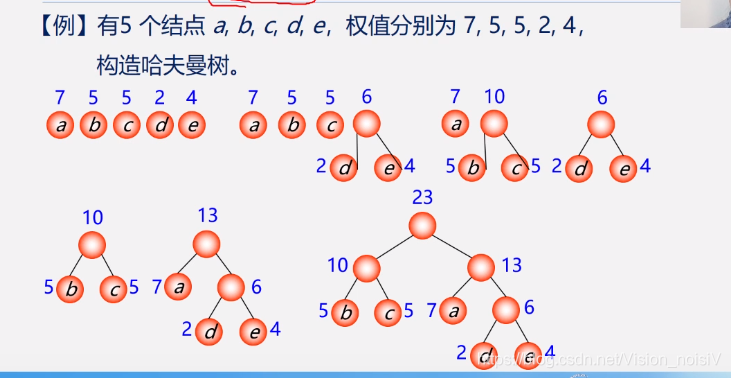

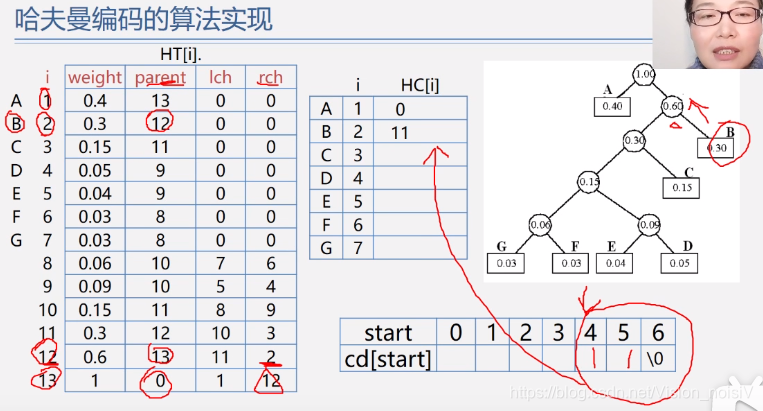
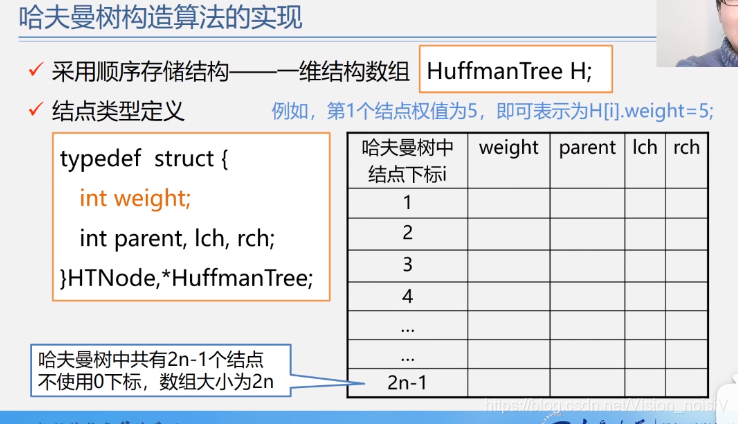
5.8.3 构造哈夫曼树算法
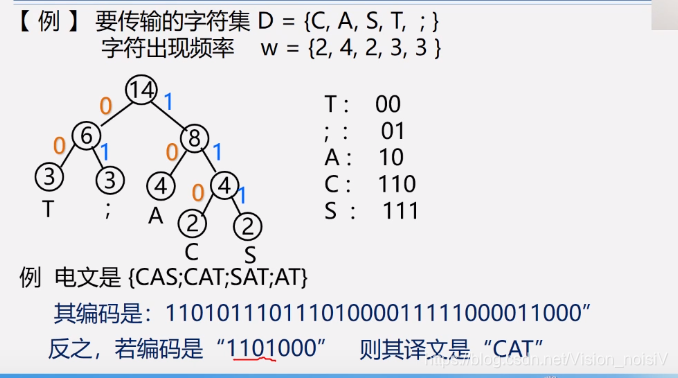
哈夫曼树主要就是一种二叉树。
对于哈夫曼树,利用顺序存储结构比链式存储结构要简单。
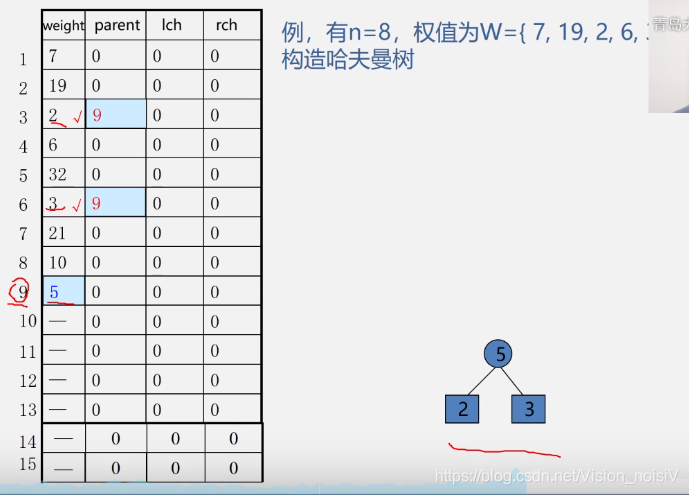
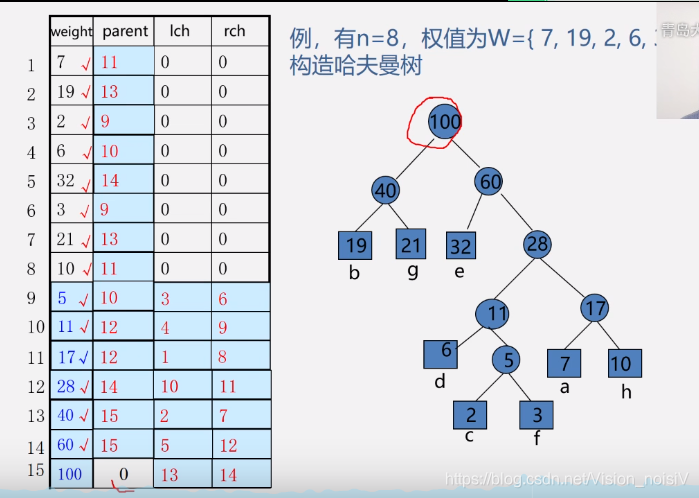
注:具体看视频。



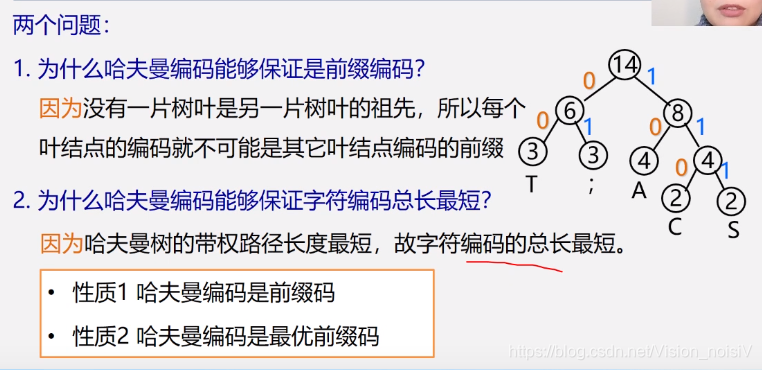
5.8.4 哈夫曼树的应用——哈夫曼编码