引言
在我看来动态规划和递归有很大的相似性,可以说动态规划就是剪枝后的递归,它舍去了递归重复的步骤,在时间复杂度上相对于递归有着非常大的提升,就比如说斐波那契数列(下题有)用递归的时间复杂度是指数级,而用动态规划则可以将其优化为线性级,且动态规划还可以继续进行优化使其空间复杂度大大减小,这就是动态规划进阶的内容了;
做动态规划类的题目有很多相似的套路和方法,开始肯定会有一些困难,题目见多了就会发现好多题有着相似的解法;
我的一般做题步骤是:
1,先找最后一步并定义一个dp[i]数组元素的含义(不一定是数组由题目而定)
2,找出关系数组间的关系式:由最后一步向前推一步,想通过哪一步(或几步)可以走到最后一步,通过这点,找到数组元素间的关系式(转移方程)
3,找出初始值(转移方程算不出的):通过转移方程来判断,有没有特殊情况无法使用转移方程,单独列出来,这就是初始值;
ps:这个方法不一定适用于所有题,一定要就题而论;
什么样的题适合动态规划求解呢?我总结有以下几种:
1,求最值类
2,求几种方法类(计数)
3,判断是否存在满足某个条件(一般布尔类型)
下面来几道有点人气的题目
斐波那契数
斐波那契数,通常用 F(n) 表示,形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是:
F(0) = 0,F(1) = 1
F(n) = F(n - 1) + F(n - 2),其中 n > 1
给你 n ,请计算 F(n) 。
示例 1:
输入:2
输出:1
解释:F(2) = F(1) + F(0) = 1 + 0 = 1
示例 2:
输入:3
输出:2
解释:F(3) = F(2) + F(1) = 1 + 1 = 2
示例 3:
输入:4
输出:3
解释:F(4) = F(3) + F(2) = 2 + 1 = 3
提示:
0 <= n <= 30
这道题就是非常经典的动态规划题目,也是递归题目,当然在有些情况下递归解题会时间超限,所以学会动态规划解法还是很重要的;
解题步骤:
1,可以设一个dp[i]的数组,是第i个数,该数组表示第i个数的和;
2,由题目可以轻松找到状态转移方程dp[i] = dp[i - 1] + dp[i - 2];
3,通过题目可以看出当i = 0时为dp[0] = 0,而且状态转移方程当i小于2时并不满足,所以单独列出特殊情况:dp[1] = dp[2] = 1;
代码如下:
int fib(int N) {
vector<int> dp(N + 1, 0);
dp[1] = dp[2] = 1;
for (int i = 3; i <= N; i++)
dp[i] = dp[i - 1] + dp[i - 2];
return dp[N];
}
我们还可以将空间复杂度从O(n)优化到O(1),该怎么做呢?我们分析可以发现,每次dp[i]加的值总是它的前两个,所以我们只需要记录前两个值,并不断更新这两个值就可以了;
代码如下:
class Solution {
public:
int fib(int n) {
int a = 0, b = 1, sum;
for (int i = 0; i < n; ++i) {
sum = a + b;
a = b;
b = sum;
}
return a;//最后通过多走一步使sum结果值赋给a,前面就不用写判断了
}
};
来到相似的题练习下:
第 N 个泰波那契数
泰波那契序列 Tn 定义如下:
T0 = 0, T1 = 1, T2 = 1, 且在 n >= 0 的条件下 Tn+3 = Tn + Tn+1 + Tn+2
给你整数 n,请返回第 n 个泰波那契数 Tn 的值。
示例 1:
输入:n = 4
输出:4
解释:
T_3 = 0 + 1 + 1 = 2
T_4 = 1 + 1 + 2 = 4
示例 2:
输入:n = 25
输出:1389537
提示: 0 <= n <= 37
答案保证是一个 32 位整数,即 answer <= 2^31 - 1。
一样的题意,思路就不写了直接上代码:
class Solution {
public:
int tribonacci(int n) {
int dp[n + 1];
if (n < 3) return n == 0? 0 : 1;
dp[0] = 0;
dp[1] = dp[2] = 1;
for (int i = 3; i <= n; ++i)
dp[i] = dp[i - 3] + dp[i - 2] + dp[i - 1];
return dp[n];
}
};
优化版本
class Solution {
public:
int tribonacci(int n) {
int sum, x = 0, y = 1, z = 1;
for (int i = 0; i < n; ++i) {
sum = x + y + z;
x = y;
y = z;
z = sum;
}
return x;
}
}
连续子数组的最大和
输入一个整型数组,数组中的一个或连续多个整数组成一个子数组。求所有子数组的和的最大值。
要求时间复杂度为O(n)。
示例1:
输入: nums = [-2,1,-3,4,-1,2,1,-5,4]
输出: 6
解释: 连续子数组 [4,-1,2,1] 的和最大,为 6。
提示:
1 <= arr.length <= 10^5
-100 <= arr[i] <= 100
这是一道求最值的题,非常经典的动态规划,来分析一下题目
1,dp[i]为nums数组中第i个数的最大值;
2,dp[i] = max(dp[i - 1] + nums[i], nums[i]);当前最大值为前一个最大值加上当前nums的值与当前nums值的最大值,防止dp[i-1]为负数;
3,dp[0] = nums[0];
代码如下:
class Solution {
public:
int maxSubArray(vector<int>& nums) {
vector<int> dp(nums.size());
int Max = dp[0] = nums[0];
for (int i = 1; i <nums.size(); ++i) {
dp[i] = max(dp[i - 1] + nums[i], nums[i]);
Max = max(Max, dp[i]);
}
return Max;
}
};
还有其他几种方法,思想类似,一块放出来了
方法2
class Solution {
public:
int maxSubArray(vector<int>& nums) {
int max = INT_MIN, sum = 0;
for (int i = 0; i < nums.size(); ++i){
sum += nums[i];
if(max < sum)
max = sum;
if(sum < 0)
sum = 0;
}
return max;
}
};
方法3
class Solution {
public:
int maxSubArray(vector<int>& nums) {
int res = nums[0];
for (int i = 1; i < nums.size(); ++i) {
nums[i] += max(0, nums[i-1]);
res = max(nums[i], res);
}
return res;
}
};
方法4
class Solution {
public:
int maxSubArray(vector<int>& nums) {
int pre = 0, ans = nums[0];
for (int i = 0; i < nums.size(); ++i) {
pre = max(pre + nums[i], nums[i]);
ans = max(ans, pre);
}
return ans;
}
};
哪个好理解看哪个
最小路径和
给定一个包含非负整数的 m x n 网格 grid ,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
说明:每次只能向下或者向右移动一步。
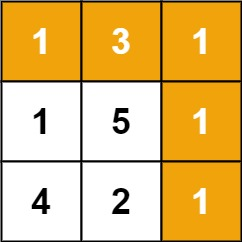
示例 1:
输入:grid = [[1,3,1],[1,5,1],[4,2,1]]
输出:7
解释:因为路径 1→3→1→1→1 的总和最小。
示例 2:
输入:grid = [[1,2,3],[4,5,6]]
输出:12
提示:
m == grid.length
n == grid[i].length
1 <= m, n <= 200
0 <= grid[i][j]<= 100
这道题同样是求最值问题,思路很简单,
1,dp[i][j]为到第i行j列的格子的最小和;
2,dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + grid[i][j];要不上一行最小,要不上一列最小,最小值加上现在格子的值;
3,dp[0][0] = grid[0][0],且当行为0时(dp[0][i])只能朝右走,列为0时(dp[i][0])只能朝左走;
代码如下:
class Solution {
public:
int minPathSum(vector<vector<int>>& grid) {
int m = grid.size(), n = grid[0].size();
int dp[m][n];
dp[0][0] = grid[0][0];
for (int i = 1; i < n; ++i)
dp[0][i] = dp[0][i - 1] + grid[0][i];
for (int i = 1; i < m; ++i)
dp[i][0] = dp[i - 1][0] + grid[i][0];
for (int i = 1; i < m; ++i) {
for (int j = 1; j < n; ++j)
dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j];
}
return dp[m - 1][n - 1];
}
};
零钱兑换
给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。
计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。
你可以认为每种硬币的数量是无限的。
示例 1:
输入:coins = [1, 2, 5], amount = 11
输出:3
解释:11 = 5 + 5 + 1
示例 2:
输入:coins = [2], amount = 3
输出:-1
示例 3:
输入:coins = [1], amount = 0
输出:0
示例 4:
输入:coins = [1], amount = 1
输出:1
示例 5:
输入:coins = [1], amount = 2
输出:2
提示:
1 <= coins.length <= 12
1 <= coins[i] <= 231 - 1
0 <= amount <=104
这道题是腾讯的一道面试题,也是完全背包问题,非常经典,同样是求最值,思路如下:
1,dp[i]是金额为i的情况下的最少硬币数;即填满容量为i的背包最少需要最少硬币数;
2,dp[i] = min(dp[i - coins[j]] + 1, dp[i]);当前填满容量i最少需要的硬币 = min( 之前填满容量i最少需要的硬币, 填满容量 i - coin 需要的硬币 + 1个当前硬币)
3,dp[0] = 0;当dp[i]为INT_MAX说明无法组合,为-1;
代码如下:
class Solution {
public:
int coinChange(vector<int>& coins, int amount) {
vector<int> dp(amount + 1);
dp[0] = 0;
int n = coins.size();
for (int i = 1; i <= amount; i++) {
dp[i] = INT_MAX;
for (int j = 0; j < n; j++) {
if(i >= coins[j] && dp[i - coins[j]] != INT_MAX)
dp[i] = min(dp[i - coins[j]] + 1, dp[i]);
}
}
if (dp[amount] == INT_MAX)
dp[amount] = -1;
return dp[amount];
}
};
编辑距离
给你两个单词 word1 和 word2,请你计算出将 word1 转换成 word2 所使用的最少操作数 。
你可以对一个单词进行如下三种操作:
插入一个字符
删除一个字符
替换一个字符
示例 1:
输入:word1 = “horse”, word2 = “ros”
输出:3
解释:
horse -> rorse (将 ‘h’ 替换为 ‘r’)
rorse -> rose (删除 ‘r’)
rose -> ros (删除 ‘e’)
示例 2:
输入:word1 = “intention”, word2 = “execution”
输出:5
解释:
intention -> inention (删除 ‘t’)
inention -> enention (将 ‘i’ 替换为 ‘e’)
enention -> exention (将 ‘n’ 替换为 ‘x’)
exention -> exection (将 ‘n’ 替换为 ‘c’)
exection -> execution (插入 ‘u’)
提示:
0 <= word1.length,
word2.length <= 500
word1 和 word2 由小写英文字母组成
这也是一道求最值问题,但是题目含有字符串,大部分字符串题目都可以用动态规划,且一般是二维数组,分析如下:
1,dp[i] [j]是,当字符串 word1 的长度为 i,字符串 word2 的长度为 j 时,将 word1 转化为 word2 所使用的最少操作次数为 dp[i] [j]。
2,dp[i] [j] = dp[i-1] [j-1],此时两个字符串相同
dp[i] [j] = min(dp[i-1] [j-1],dp[i] [j-1],dp[i-1] [j]) + 1
这个是分了三种情况:
2.1,dp[i-1] [j-1]是替换字符时进行的操作
2.2,dp[i] [j-1]是word1插入时的操作
2.3,dp[i-1] [j]是word1删除时的操作
3,初始值是计算出所有的 dp[0] [0….n] 和所有的 dp[0….m] [0],因为i和j为0时转移方程便无法使用;
代码如下:
class Solution {
public:
int minDistance(string word1, string word2) {
int len1 = word1.length();
int len2 = word2.length();
vector<vector<int>> dp(len1 + 1, vector<int>(len2 + 1));
for (int j = 1; j <= len2; ++j) dp[0][j] = dp[0][j - 1] + 1;//word1为空
for (int i = 1; i <= len1; ++i) dp[i][0] = dp[i - 1][0] + 1;//word2为空
for (int i = 1; i <= len1; ++i) {
for (int j = 1; j <= len2; ++j) {
if (word1.at(i - 1) == word2.at(j - 1))//word1 ==word2
dp[i][j] = dp[i - 1][j - 1];
else
dp[i][j] = min(min(dp[i - 1][j], dp[i][j - 1]), dp[i - 1][j - 1]) + 1;
}
}
return dp[len1][len2];
}
};
爬楼梯
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
注意:给定 n 是一个正整数。
示例 1:
输入: 2
输出: 2
解释: 有两种方法可以爬到楼顶。
1 阶 + 1 阶
2 阶
示例 2:
输入: 3
输出: 3
解释: 有三种方法可以爬到楼顶。
1 阶 + 1 阶 + 1 阶
1 阶 + 2 阶
2 阶 + 1 阶
这道题就是一道计数类的动态规划问题,我们通过审题可以发现,这个题就是一个斐波那契数列,那就没有什么可说的的了,一样的代码,再来一遍:
class Solution {
public:
int climbStairs(int n) {
int dp[n+1];
dp[0] = 1;
dp[1] = 1;
for (int i = 2; i <= n; ++i)
dp[i] = dp[i - 1] + dp[i - 2];//这里dp[i]是爬到第i阶有几种方法
return dp[n];
}
};
不同路径
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
示例 1:
输入:m = 3, n = 7
输出:28
示例 2:
输入:m = 3, n = 2
输出:3
解释:
从左上角开始,总共有 3 条路径可以到达右下角。
向右 -> 向下 -> 向下
向下 -> 向下 -> 向右
向下 -> 向右 -> 向下
示例 3:
输入:m = 7, n = 3
输出:28
示例 4:
输入:m = 3, n = 3
输出:6
提示: 1 <= m, n <= 100
题目数据保证答案小于等于 2 * 109
这道题也是一道计数类的题,让求多少种不同的路径,分析如下:
1,dp[i][j]是到第i行第j列的格子所有的路径数;
2,dp[i][j] = dp[i - 1][j] + dp[i][j - 1];我们只能朝下或者朝右走,所以dp[i][j]格子的前一个格子只会是dp[i - 1][j]或者dp[i][j - 1],它俩路径数之和就是当前格子路径数;
3,当i为0时或者j为0时,转移方程不成立,所以我们单独分析,当i为0时即为第一行,能走到右下角最后一个格子的路径只有沿边缘的一条,即为dp[0][j] = 1,同理dp[i][0] = 1;
代码如下:
class Solution {
public:
int uniquePaths(int m, int n) {
vector<vector<int>> dp(m, vector<int>(n));
int i, j;
for (i = 0; i < m; ++i) {
for (j = 0; j < n; ++j) {
if (!i || !j)
dp[i][j] = 1;
else
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
return dp[i - 1][j - 1];
}
};
不同路径 II
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为“Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为“Finish”)。
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径?
网格中的障碍物和空位置分别用 1 和 0 来表示。
示例 1:

输入:obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
输出:2
解释:
3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径:
向右 -> 向右 -> 向下 -> 向下
向下 -> 向下 -> 向右 -> 向右
示例 2:

输入:obstacleGrid = [[0,1],[0,0]]
输出:1
提示:
m == obstacleGrid.length
n == obstacleGrid[i].length
1 <= m, n <=100
obstacleGrid[i][j] 为 0 或 1
这道题相对上一道题多了障碍物,但是都是一样的思路,只需要多加上判断障碍物的条件就可以了,直接上代码:
class Solution {
public:
int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
int m = obstacleGrid.size(), n = obstacleGrid[0].size();
vector<vector<int>> dp(m, vector<int> (n));
int i, j;
for (i = 0; i < m && !obstacleGrid[i][0]; ++i)
dp[i][0] = 1;
for (j = 0; j < n && !obstacleGrid[0][j]; ++j)
dp[0][j] = 1;
for (i = 1; i < m; ++i) {
for (j = 1; j < n; ++j) {
if(!obstacleGrid[i][j])//若当前位置没有障碍物
dp[i][j] = dp[i-1][j] + dp[i][j-1];
}
}
return dp[m-1][n-1];
}
};
跳跃游戏
给定一个非负整数数组 nums ,你最初位于数组的 第一个下标 。
数组中的每个元素代表你在该位置可以跳跃的最大长度。
判断你是否能够到达最后一个下标。
示例 1:
输入:nums = [2,3,1,1,4]
输出:true
解释:可以先跳 1 步,从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。
示例 2:
输入:nums = [3,2,1,0,4]
输出:false
解释:无论怎样,总会到达下标为 3 的位置。但该下标的最大跳跃长度是 0 , 所以永远不可能到达最后一个下标。
提示:
1 <= nums.length <= 3 * 104
0 <= nums[i] <= 105
这道题其实时一道经典的贪心算法题,但是动态规划也可以解决,这道题就属于动态规划中的判断类的题目;
1,dp[i]表示是否能达到第i阶
2,这个有点特殊就是可以将状态方程作为一个条件,当可以达到dp[i]的前一阶且前一阶可以达到dp[i]时,让dp[i]为true;
3,dp[0] = true,其他情况开始先赋一个初始值false;
代码如下:
class Solution {
public:
bool canJump(vector<int>& nums) {
int n = nums.size();
vector<bool> dp(n);
dp[0] = true;
//i是阶数,j是i的前一阶
for (int i = 1; i < n; ++i) {
dp[i] = false;
for (int j = i - 1; j >= 0; --j) {
if (dp[j] && j + nums[j] >= i) {
dp[i] = true;
break;
}
}
}
return dp[n-1];
}
};
这就是几道动态规划的小题,当然动态规划依然有好多不同的类型,只要多做题总结,就能发现其中的套路了