一、单变量房价预测
采用一元线性回归实现单变量房价预测。通过房屋面积与房价建立线性关系,通过梯度下降进行训练,拟合权重和偏置参数,使用训练到的参数进行房价预测。
1、房屋面积与房价数据
| 32.50234527 | 31.70700585 |
| 53.42680403 | 68.77759598 |
| 61.53035803 | 62.5623823 |
| 47.47563963 | 71.54663223 |
| 59.81320787 | 87.23092513 |
| 55.14218841 | 78.21151827 |
| 52.21179669 | 79.64197305 |
| 39.29956669 | 59.17148932 |
| 48.10504169 | 75.3312423 |
| 52.55001444 | 71.30087989 |
| 45.41973014 | 55.16567715 |
| 54.35163488 | 82.47884676 |
| 44.1640495 | 62.00892325 |
| 58.16847072 | 75.39287043 |
| 56.72720806 | 81.43619216 |
| 48.95588857 | 60.72360244 |
| 44.68719623 | 82.89250373 |
| 60.29732685 | 97.37989686 |
| 45.61864377 | 48.84715332 |
| 38.81681754 | 56.87721319 |
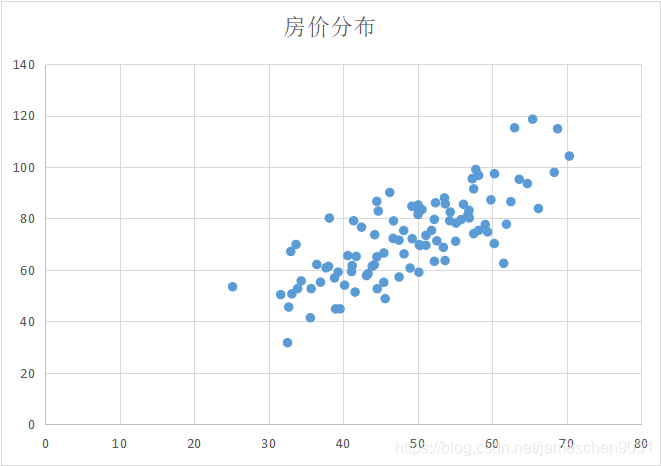
2、面积与房价分布散点图
3、实现步骤。
训练部分:
第一步,数据预处理,采用归一化。
第二步,建立线性关系,y=w*x+b,y为房价,x为面积,w权重,b偏置。
第三步,通过偏导数计算梯度。w_gradient=SUM(2*x*((w*x+b)-y) / N),b_gradient=SUM(2*((w*x+b)-y) / N),N为训练数据个数。初始化权重和偏置,一般初始化为0,通过偏导数计算权重和偏置的梯度,通过梯度和学习率更新权重和偏置。
第四步,计算误差,采用均方差计算全局误差。
实现代码:
import numpy as np
#计算误差
def compute_error(w, b, points):
????total_error = 0
????for i in range(0, len(points)):
????????x = points[i, 0]
????????y = points[i, 1]
????????total_error += (y - (w * x + b)) ** 2
????return total_error / float(len(points))
#计算梯度
def step_gradient(w_current, b_current, points, learn_Rate):
????b_gradient = 0
????w_gradient = 0
????N = float(len(points))
????for i in range(0, len(points)):
????????x = points[i, 0]
????????y = points[i, 1]
????????b_gradient += (2/N) * ((w_current * x + b_current) - y)
????????w_gradient += (2/N) * ((w_current * x + b_current) - y) * x
????new_b = b_current - (learn_Rate * b_gradient)
????new_w = w_current - (learn_Rate * w_gradient)
????return [new_b, new_w]
#梯度下降,循环计算权重和偏置
def gradient_descent_runner(points, starting_w, starting_b, learn_rate, iteration_num):
????b = starting_b
????w = starting_w
????for i in range(iteration_num):
????????b, w = step_gradient(w, b, np.array(points), learn_rate)
????return [b, w]
#导入数据,开始计算
def run():
????points = np.genfromtxt("data0.csv", delimiter=",")
????learn_rate = 0.0001
????initial_b = 0
????initial_w = 0
????iteration_num = 2000
????print("start gradient b = {0}, w = {1}, error = {2}"
??????????.format(initial_b, initial_w, compute_error(initial_w, initial_b, points)))
????[b, w] = gradient_descent_runner(points, initial_w, initial_b, learn_rate, iteration_num)
????print("after iteration b = {0}, w = {1}, error = {2}"
??????????.format(b, w, compute_error(w, b, points)))
if __name__ == '__main__':
????run()
测试部分:
#偏置、权重和输入值
def predict(b, w, x):
????return w*x + b
if __name__ == '__main__':
????print(predict(0.5523011954231988, 1.2331875596916462, 90))
二、多变量房价预测
在面积基础上增加一维房间数,将单变量预测改为多变量预测。
| 2104 | 3 | 399900 |
| 1600 | 3 | 329900 |
| 2400 | 3 | 369000 |
| 1416 | 2 | 232000 |
| 3000 | 4 | 539900 |
| 1985 | 4 | 299900 |
| 1534 | 3 | 314900 |
| 1427 | 3 | 198999 |
| 1380 | 3 | 212000 |
| 1494 | 3 | 242500 |
| 1940 | 4 | 239999 |
| 2000 | 3 | 347000 |
| 1890 | 3 | 329999 |
| 4478 | 5 | 699900 |
| 1268 | 3 | 259900 |
| 2300 | 4 | 449900 |
| 1320 | 2 | 299900 |
| 1236 | 3 | 199900 |
| 2609 | 4 | 499998 |
| 3031 | 4 | 599000 |
采用多元线性回归实现。根据偏导数的计算公式,w_gradient=SUM(2*x*((w*x+b)-y) / N),假设x恒为1,该公式即变换为偏置参数的计算公式。只需要对训练数据加一列值1,即x=1,该列数据对应偏置参数,即可将偏置的计算归入到权重计算方式中,实现一元线性回归和多元线性回归的统一。
实现代码:
import numpy as np
#计算误差
def compute_error(w, points):
????total_error = 0
????for i in range(0, len(points)):
????????x = np.zeros(len(w))
????????for j in range(0, len(w)):
????????????x[j] = points[i, j]
????????y = points[i, len(w)]
????????y_predict = 0.
????????for j in range(0, len(w)):
????????????y_predict += w[j] * x[j]
????total_error += (y - y_predict) ** 2
????return total_error / float(len(points))
#计算梯度
def step_gradient(w_current, points, learn_rate):
????w_gradient = np.zeros(len(w_current))
????new_w = np.zeros(len(w_current))
????N = float(len(points))
????for i in range(0, len(points)):
????????x = np.zeros(len(w_current))
????????for j in range(0, len(w_current)):
????????????x[j] = points[i, j]
????????y = points[i, len(w_current)]
????????y_predict = 0.
????????for j in range(0, len(w_current)):
????????????y_predict += w_current[j] * x[j]
????????for j in range(0, len(w_current)):
????????????w_gradient[j] = 2 * x[j] * (y_predict - y) / N
????????for j in range(0, len(w_current)):
????????????new_w[j] = w_current[j] - (learn_rate * w_gradient[j])
????return new_w
#梯度下降,循环计算权重和偏置
def gradient_descent_runner(points, starting_w, learn_rate, iteration_num):
????w = starting_w
????for i in range(iteration_num):
????????w = step_gradient(w, np.array(points), learn_rate)
????return w
#导入数据,开始计算
def run():
????points = np.genfromtxt("data0.csv", delimiter=",")
????learn_rate = 0.0001
????initial_w = np.zeros(3)
????iteration_num = 20000
????initial_error = compute_error(initial_w, points)
????print(initial_error)
????w = gradient_descent_runner(points, initial_w, learn_rate, iteration_num)
????error = compute_error(w, points)
????print(error)
if __name__ == '__main__':
????run()