[数据结构与算法]2021牛客暑期多校训练营2——G、League of Legends

看了官方题解视频，觉得有*点简略，和评论区的感觉一样(

这里重新写一篇连铜牌都能看懂的 题解。

题意

给定 n 个区间 [ai,bi)，要求将它们分成 k 组，最大化每组交的长度之和，并且每组的交长度不能为0。1≤k≤n≤5000 ， 1≤a<b<105 。

思路

对于包含其他区间的大区间，我们考虑两种情况对其进行分配
1.归属到一个被它包含的区间所在的组，不影响答案
2.独自一组，长度直接算入答案
很显然，要么为第一种情况，要么为第二种情况，因此可以单独处理。
剩下的就是互不从属的小区间，我们令$d{p}_{i,j}$代表前j个数分成i组的交长度和，$(a_i,b_i)$代表剩下的小区间。
而每次转移只考虑最后一个多出来的组从哪(下标为k)开始
也就是可以写为
$$dp[i][j]=dp[i?1][k]+b_{k+1}?a_j$$
其图示如下

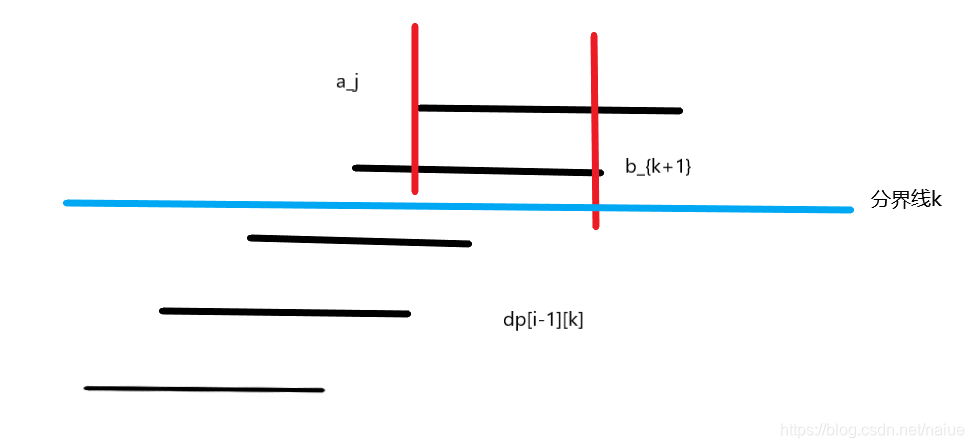
显然，按照一般的枚举方式，我们需要分别枚举i，j，k三个维度。
此时的复杂度将会高达$O(n^3)$
但我们观察发现：
原转移方程可以改写为
$$dp[i][j]=max(dp[i?1][k]+b_{k+1})?a_j,when{b}_{k+1}>a_j$$
显然$max(dp[i?1][k]+b_{k+1})$是可以使用单调队列进行维护最大值的。
不会维护的以及不知道为什么能优化的，请看这个博客中的例子：
https://www.cnblogs.com/ljy-endl/p/11638389.html
最后，我们再综合一下之前预处理的那些大区间，就得到了最后的答案。
代码：

#include<bits/stdc++.h>
using namespace std;
const int N = 5e3+5;
struct node{
    int l,r;
}a[N*2],small[N*2];/*small 存储小区间*/
int bL[N],q[N],dp[N][N];/*bL 大区间*/
int main()
{
    memset(dp,-1,sizeof dp);
    int n,k;
    cin>>n>>k;
    for(int i=1;i<=n;i++)cin>>a[i].l>>a[i].r;
    sort(a+1,a+n+1,[=](node x,node y){
        return x.l!=y.l?x.l<y.l:x.r>y.r;
    });
    int maxn = 0x3f3f3f3f;
    int cnt=0,tot=0;
    for(int i=n;i>0;i--)//处理大区间和小区间
    {
        if(a[i].r>=maxn)bL[++cnt] = a[i].r-a[i].l;
        else maxn = a[i].r,small[++tot]=a[i];
    }
    reverse(small+1,small+tot+1);
    sort(bL+1,bL+cnt+1,greater<int>());
    dp[0][0]=0;
    for(int i=1;i<=k;i++)
    {
        int h=1,t=0;
        for(int j=1;j<=tot;j++)
        {
            if(dp[i-1][j-1]>-1){//当最后一次转移合法
                while (h<=t&&
                    dp[i-1][q[t]]+small[q[t]+1].r<=dp[i-1][j-1]+small[j].r)
                    	t--;//队尾维护max(dp[i-1][k]+b_{k+1})
                q[++t]=j-1;
            }
            while (h<=t&&small[q[h]+1].r<=small[j].l)h++;//队首维护b_{k+1} >a_j
            if(h<=t)dp[i][j]=dp[i-1][q[h]]+small[q[h]+1].r-small[j].l;//找出了最优的max 所需的K，进行状态转移
        }
    }
    int tmp=0,ans=0;
    for(int i=0;i<=min(k,n);i++)
    {
        tmp+=bL[i];
        if(dp[k-i][tot]>-1){//所有小区间分成k-i段合法，此时还可包含i个大区间
            ans = max(ans,dp[k-i][tot]+tmp);
        }
    }
    cout<<ans<<endl;
}