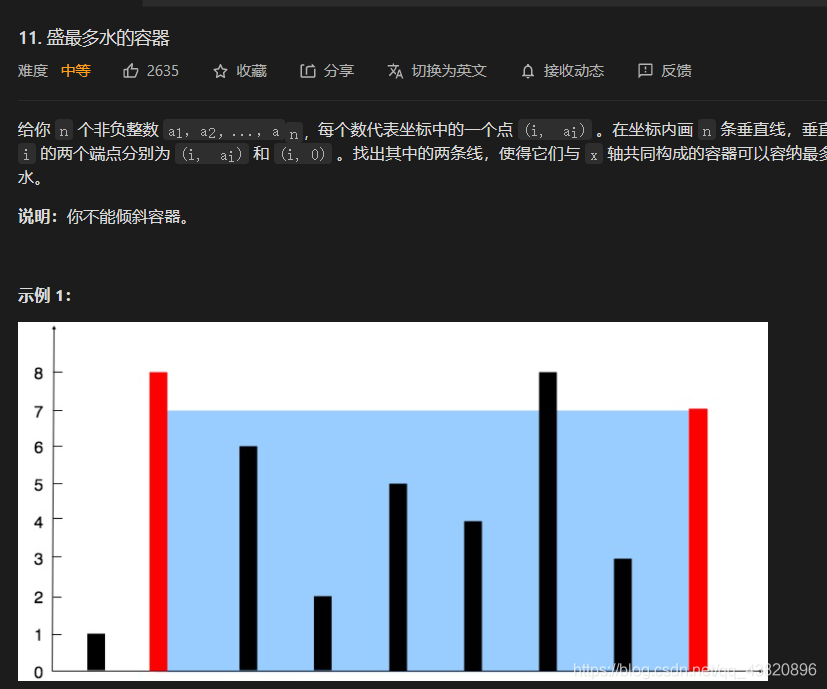
题目

在这里插入图片描述
题目链接

一、解题思路

这题其实就是要求那两个点的面积最大。有两种解题思路。

1. 暴力破解

通过两层循环遍历任意两点的所有组合情况，然后求出两点的面积值，然后取最大值。
这种方法是最容易想到的。但是当我们使用这种方法提交上去时，会出现超时错误。不要问我为什么！！！懂得都懂。所以我们要通过一种要想出一种时间复杂度更低的方法。

2.双指针法

首先双层循环时肯定不行的，所以我们就来试试单层循环。单层循环我们要获取最大的面积我们首先要确定如何遍历。这点很关键!!!我们不能再向之前双层循环从头遍历到尾。单层循环我们需要通过从两头开始遍历。那这就产生了一种限制。我们每次往中间移的话长度都是再变小！！！然后我们又不希望要获取面积的慢慢随着长度的变小而变小，所以我们需要让我们的高度变高。而高度是由较小的高度来决定，所以我们要让高度变大，只需要让高度较小的一番往中间移。当两条线重合或者超过的时候就遍历完了。

二、方法代码

//暴力破解
 public int maxArea(int[] height) {

    int maxArea = 0;
   
    for (int i = 0; i < height.length - 1; i++) {
      for (int j = i + 1; j < height.length; j++) {
        int largeHeight = height[i] > height[j] ? height[j] : height[i];
        int area = largeHeight * (j - i);
        System.out.println();
        if (area > maxArea) {
          maxArea = area;
        }
      }
      //
    }
    return maxArea;
  }

///双指针法
 public int maxArea(int[] height) {

    int maxArea = 0;
    int i = 0;
    int j = height.length - 1;
    for (; i < j; ) {
      int area;
      if (height[i] <= height[j]) {
        area = height[i] * (j - i);
        i++;
      } else {
        area = height[j] * (j - i);
        j--;
      }
      if (maxArea < area) {
        maxArea = area;
      }
    }
    return maxArea;
  }