算法学习
1、数据结构
存储数据的不同方式。
2、算法
同一问题的不同解决方法。(算法往往是针对特定数据结构的。)
算法的优劣
时间复杂度:随着问题规模的变化而时间变化的规律。
空间复杂度:随着问题规模的变化而空间变化的规律。
3、 Big O
时间-问题(数据)规模
- 不考虑必须要做的操作
循环、赋初值、程序初始化…… - 不考虑常数项
- 不考虑低次项
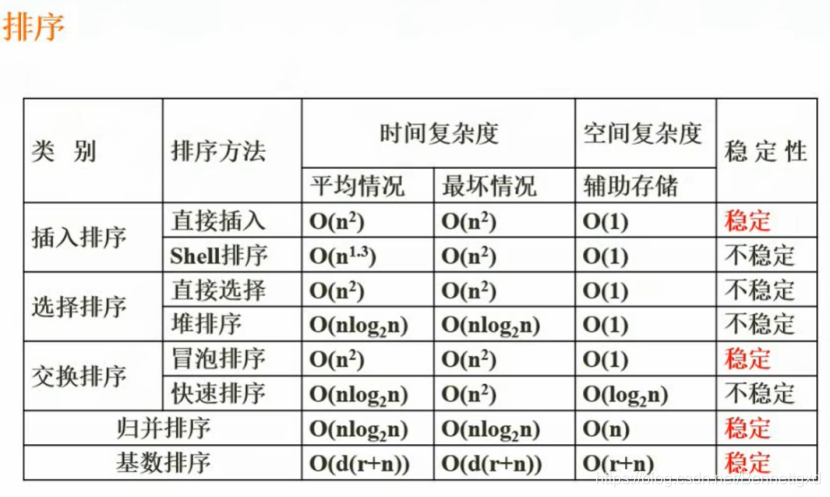
常见排序列表
| 中文名称 | 英文名称 | 平均时间复杂度 | 最坏时间复杂度 | 最好时间复杂度 | 空间复杂度 | 稳定性 |
|---|---|---|---|---|---|---|
| 选择排序 | Selection | n2 | n2 | n2 | 1 | N |
| 冒泡排序 | Bubble | n2 | n2 | n | 1 | Y |
*插入排序 | Insertion | n2 | n2 | n | 1 | Y |
*堆排序 | Heap | n log2n | n log2n | n log2n | 1 | N |
| 希尔排序 | Shell | n1.3 | n2 | n | 1 | N |
*归并排序 | Merge | n log2n | n log2n | n log2n | n | Y |
*快速排序 | Quick | n log2n | n2 | n log2n | log2n | N |
| 桶排序 | Buckel | n + k | n2 | n | n + k | Y |
| 计数排序 | Counting | n + k | n + k | n + k | n + k | Y |
| 基数排序 | Radix | n * k | n * k | n * k | n + k | Y |
(注意:Y:稳定,N:不稳定。)
如何编写算法程序
- 有简单到复杂
验证一步走一步
多打印中间结果 - 先局部后整体
没思路时先细分 - 先粗糙后精细
变量更名
语句合并
边界处理
简单排序
1、选择排序
package Tests;
public class Test1 {
/*
* 选择排序
*
* */
public static void main(String[] args) {
int[] arrays = { 4, 6, 7, 2, 8, 1, 9, 3, 5 };
// 排序前
System.out.println("排序前:");
for (int i = 0; i < arrays.length; i++) {
System.out.print(arrays[i] + " ");
}
// long star = System.currentTimeMillis();
for (int j = 0; j < arrays.length; j++) {
// 1、线找到最小值的下标
int min = j;
for (int i = j + 1; i < arrays.length; i++) {
if (arrays[i] < arrays[min]) {
min = i;
}
}
// 2、将最小值的下标与第一个元素进行交换位置
int temp = arrays[j];
arrays[j] = arrays[min];
arrays[min] = temp;
}
// long end = System.currentTimeMillis();
System.out.println("\n排序后:");
for (int i = 0; i < arrays.length; i++) {
System.out.print(arrays[i] + " ");
}
// System.out.println("\nusing time:" + (end - star));
}
}
对算法的时间/空间复杂度进行分析
验证算法——对数器
DataChecker.java
package Tests;
import java.util.Arrays;
import java.util.Random;
public class DataChecker {
/*
* 第一步:创建随机数组
*/
static int[] getByRandomToArrays() {
// 1、创建一个随机数的对象
Random r = new Random();
// 2、创建数组
int[] arr = new int[20];
// 3、向数组中添加数组元素
for (int i = 0; i < arr.length; i++) {
arr[i] = r.nextInt(20);
}
return arr;
}
/*
* 第二步:系统的比较器与你的比较算法进行比较
*
*/
static void check() {
int[] arr1 = getByRandomToArrays();
// 拷贝一份随机数组
int[] arr2 = new int[arr1.length];
System.arraycopy(arr1, 0, arr2, 0, arr1.length);
// 使用系统的比较器进行数组的排序
Arrays.sort(arr1);
// 使用你的排序算法进行排序
SelectSort.sort(arr2);
/*
* 第三步:进行数组元素之间的比较
*
*/
Boolean b = true;
for (int i = 0; i < arr2.length; i++) {
// if (arr1[i] != arr2[i])
// b = false;
b = arr1[i] != arr2[i] ? false:true;
}
System.out.println(b == true ? "righr" : "wrong");
// return b;
}
// main()方法测试
public static void main(String[] args) {
check();
}
}
注意:最好是在check()进行多次的比较,对你写的算法就更加可靠。
SelectSort.java
自己定义的排序算法
package Tests;
public class SelectSort {
public static int[] sort(int[] arr3) {
for (int i = 0; i < arr3.length; i++) {
int min = i;
for (int j = i + 1; j < arr3.length; j++) {
min = arr3[j] < arr3[min] ? j : min;
}
int temp = arr3[i];
arr3[i] = arr3[min];
arr3[min] = temp;
}
return arr3;
}
}
2、冒泡排序
// 冒泡排序1
public static void bubbleSort(int arr[]) {
for (int i = 0; i < arr.length - 1; i++) {
for (int j = 0; j < arr.length - 1 - i; j++) {
if (arr[j] > arr[j + 1]) {
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
}
}
// 冒泡排序2
static void sort(int arr[]) {
for (int i = arr.length - 1; i > 0; i--) {
for (int j = 0; j < i; j++) {
if (arr[j] > arr[j + 1]) {
int temp = arr[j + 1];
arr[j + 1] = arr[j];
arr[j] = temp;
}
}
}
}
3、插入排序
package bennett.sortingAlgorithm;
public class InsertionSort {
public static void main(String[] args) {
int[] arrays = {5,3,6,8,1,7,9,4,2};
System.out.println("排序前");
print(arrays);
sort(arrays);
System.out.println("\n排序后");
print(arrays);
}
static void sort(int[] arr) {
for (int i = 0; i < arr.length; i++) { //i最好从i=1开始,因为i=0时,内层循环不执行
for (int j = i; j > 0; j--) {
if (arr[j] < arr[j - 1]) {
swap(arr, j, j - 1);
}
}
/*优化结构
for (int j = i; j > 0 && arr[j] < arr[j - 1]; j--) {
swap(arr, j, j - 1);
}
*/
}
}
//问题:为什么arr.length时,排序后将会8变为4???
static void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
public static void print(int[] a) {
for (int i = 0; i < a.length; i++) {
System.out.print(a[i]);
}
}
}
非简单排序
1、希尔排序
package bennett.sortingAlgorithm;
public class ShellSort {
public static void main(String[] args) {
int[] arrays = {9,6,11,3,5,12,8,7,10,15,14,4,1,13,2};
System.out.println("排序前");
print(arrays);
sort(arrays);
System.out.println("\n排序后");
print(arrays);
}
static void sort(int[] arr) {
// version 1.0
// shift + ctrl + /如下注释 。ctrl + / 每一个都用“//”注释
/*for(int gap = 4; gap > 0;gap /= 2){
for (int i = gap; i < arr.length; i++) {
for (int j = i; j > gap - 1; j-= gap) {
if (arr[j] < arr[j - gap]) {
swap(arr, j, j - gap);
}
}
}
}*/
// version 2.0
// 希尔最开时就是使用二分的办法来进行分组
/*for(int gap = arr.length / 2; gap > 0;gap /= 2){
for (int i = gap; i < arr.length; i++) {
for (int j = i; j > gap - 1; j-= gap) {
if (arr[j] < arr[j - gap]) {
swap(arr, j, j - gap);
}
}
}
}*/
// version 3.0
// Kunth序列
// h = 1; h = 3*h +1;
int h = 1;
while(h <= arr.length / 3){
h = 3*h + 1;
}
for(int gap = h; gap > 0;gap = (gap - 1)/3){
for (int i = gap; i < arr.length; i++) {
for (int j = i; j > gap - 1; j-= gap) {
if (arr[j] < arr[j - gap]) {
swap(arr, j, j - gap);
}
}
}
}
}
//问题:为什么arr.length时,排序后将会8变为4???
static void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
public static void print(int[] a) {
for (int i = 0; i < a.length; i++) {
System.out.print(a[i]+",");
}
}
}
2、快速排序(Quick Sort)
package bennett.sortingAlgorithm;
public class QuickSort {
public static void main(String[] args) {
int[] arr = {7,3,2,8,1,9,5,4,6};
System.out.println("排序前");
print(arr);
sort(arr,0,arr.length - 1);
System.out.println("\n排序后");
print(arr);
}
public static void sort(int[] arr, int leftBound, int rightBound) {
if (leftBound >= rightBound) return;
int mid = partition(arr,leftBound,rightBound);
sort(arr,leftBound,mid - 1);
sort(arr,mid + 1,rightBound);
}
static int partition(int[] arr, int leftBound, int rightBound){
int pivot = arr[rightBound];
int left = leftBound;
int right = rightBound - 1;
while (left <= right){
while (left <= right && arr[left] <= pivot) left ++;
while (left <= right && arr[right] > pivot) right --;
// System.out.println("left = "+left+" ;right = "+right);
if (left < right) swap(arr,left,right);
}
swap(arr,left,rightBound);
return left;
}
static void swap(int[] arr,int i,int j){
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
static void print(int[] arr){
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i]+",");
}
}
}
4、创建算法介绍
回溯法(Backtracking)
n皇后问题描述为:在一个nxn的棋盘上摆放n个皇后,要求任意两个皇后不能冲突,即任意两个皇后不在同一行、同一列或者同一斜线上
算法的基本思想如下:
将第i个皇后摆放在第i行,i从1开始,每个皇后都从第1列开始尝试。尝试时判断在该列摆放皇后是否与前面的皇后有冲突,如果没有冲突,则在该列摆放皇后,并考虑摆放下一个皇后;如果有冲突,则考虑下一列。如果该行没有合适的位置,回溯到上一个皇后,考虑在原来位置的 个位置上继续尝试摆放皇后,……直到找到所有合理摆放方案。
下面是算法的Java语言实现。
(1)常量和变量说明
n:皇后数,棋盘规模为nxn
queen[]:皇后的摆放位置数组,queen[i]表示第i个皇后的位置,1<=queen[i]<=n
public class Backtracking {
public static int n =4; //皇后的数量
public static int count = 0; //统计n皇后问题的方案数
public static int[] queen = new int[n + 1];
public static void main(String[] args) {
Nqueen(1);
System.out.println(n+"皇后问题的解法总数:"+count);
}
// 1、
public static void Nqueen(int j){
int i;
for (i = 1; i <= n; i++) {
queen[j] = i;
if (place(j)){
if (j == n){ //如果所有皇后都摆放好,则输出当前的北方方案
show();
count++;
}else{ //否则继续摆放下一个皇后
Nqueen(j + 1);
}
}
}
}
// 2、检查当前列是否可以放置皇后,不能返回false,可以摆放返回true
public static boolean place(int j){
int i;
for (i = 1;i < j;i++){ //检查与已摆放的皇后是否在同一列或者同意斜线上
if (queen[i]==queen[j]||Math.abs(queen[i] - queen[j]) == (j - i)){
return false;
}
}
return true;
}
// 3、输出所有皇后摆放的方案
public static void show(){
int i;
System.out.print("(");
for (i = 1; i <= n; i++) {
System.out.print(queen[i]);
}
System.out.print(")\n");
}
}
