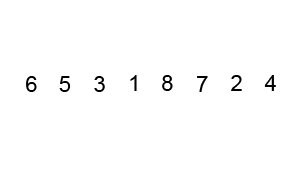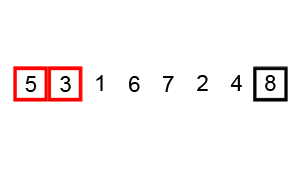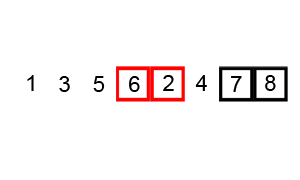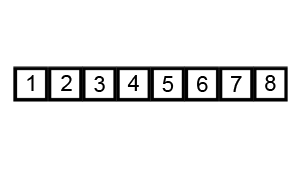开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 数据结构与算法 -> 考研数据结构笔记——第八章排序 -> 正文阅读

[数据结构与算法]考研数据结构笔记——第八章排序

?文章目录：

一：插入排序

?

?

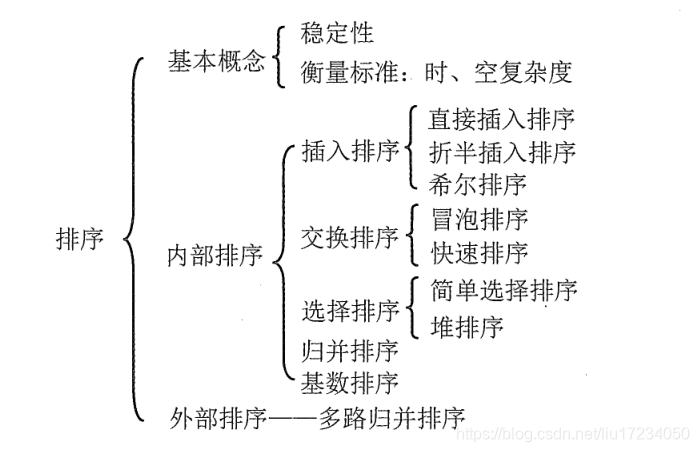
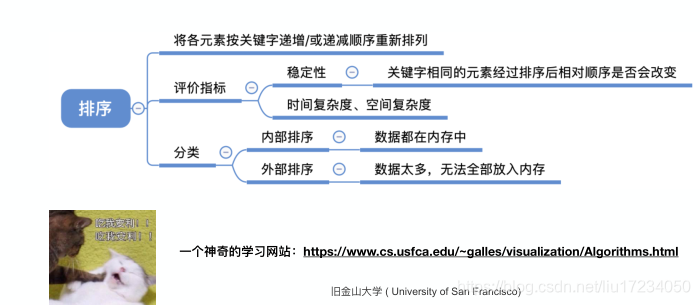
内部排序：数据都在内存（关注如何使算法时间、空间复杂度更低）

外部排序：数据太多，无法全部放入内存（还要关注如何使读/写磁盘次数更少）

稳定性：关键字相同的元素经过排序后相对顺序是否发生变化

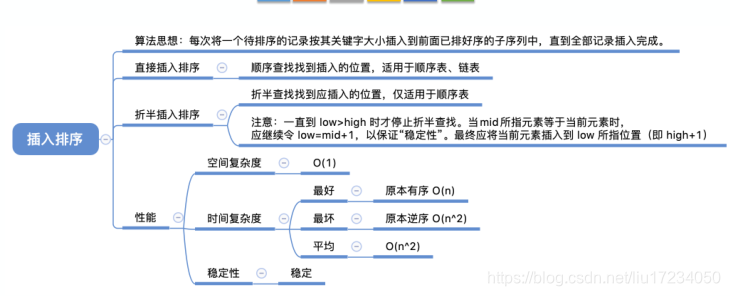
一：插入排序

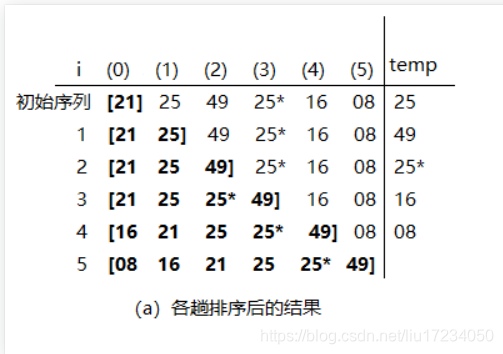
1.直接插入排序

顺序查找找到插入的位置，适用于顺序表、链表?

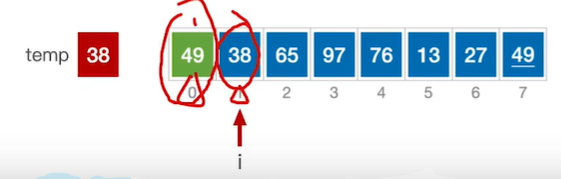
1.1 不带哨兵的

思想：
    总共有n个数据元素?????????变量i，指向当前需要插入到前边的序列元素

    只有当前处理的元素，比他前面更加小的时候，我们才需要移动前面的元素

    因为当前i的值会改变，所以先用数组保存起来，防止移动数据发生覆盖

    从i的左边依次往左检查比当前元素更大，大就交换位置,j--当j<0的时候就会停止




//直接插入排序
void InsertSort(int A[],int n)
{
    int i,j,temp;
    for( i=1; i<n; i++)    //将各元素插入已排好序的序列中
        if(A[i]<A[i-1])   //若A[i]关键字小于前驱
        {
             temp=A[i];    //用temp暂存A[i]
            for(j=i-1;j>=0 && A[j]>temp;--j)    //检查所有前面已排好序的元素
                A[j+1]=A[j];                    //所有大于temp的元素都向后挪位
            A[j+1]=temp;                        //复制到插入位置
        }
}

template<class T>
void InsertSort(T* array, int n) {               //array待排序数组,n:数组元素数量
    int i, j;                                    //循环变量
    T temp;                                      //存储待排序元素
    for (i = 1; i < n; i++) {                    //将各个元素插入已经排好的序列中
        j = i;
        temp = array[i];                         //待排序元素赋值给临时变量
        while (j > 0 && temp < array[j - 1]) {   //当未达到数组的第一个元素或者待插入元素小于当前元素
            array[j] = array[j - 1];             //就将该元素后移
            j--;                                 //下标减一，继续比较
        }
        array[j] = temp;                         //插入位置已经找到，立即插入
    } 
}

#include <iostream>

using namespace std;

void InsertSort(int *a) {
    for (int i = 1; i < 10; ++i) {//共进行n-1趟
        int temp = a[i];
        int j;
        for (j = i - 1; j >= 0 && temp < a[j]; --j) {//往前面i-1个有序元素中插入a[i]
            a[j + 1] = a[j]; //后移
        }
        a[j + 1] = temp;
    }
}

int main() {
    int a[10] = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9};
    InsertSort(a);
    for (int i = 0; i < 10; ++i) {
        cout << a[i] << " ";
    }
    return 0;
}

?时间复杂度为O(n^2)?

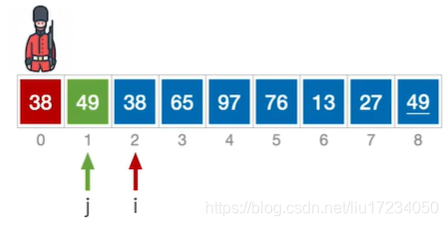
1.2 带哨兵的

把0的位置空出来作为哨兵?

/直接插入排序（带哨兵)
    void InsertSort(int A[],int n)
    {
        int i,j;
        for( i=2 ; i<=n; i++)    //依次将A[2]~A[n]插入到前面已排序序列
            if(A[i]<A[i-1])      //若A[i]关键码小于其前驱，将A[i]插入有序表
            {
                 A[0]=A[i];       //复制为哨兵，A[0]不存放元素
                 for(j=i-1;A[0]<A[j];--j)    //从后往前查找待插入位置
                    A[j+1]=A[j];             //向后挪位
                 A[j+1]=A[0];                //复制到插入位置
            }
    }

空间复杂度：O(1)

最好时间复杂度—— O(n)

最坏时间复杂度——O(n 2 )

平均时间复杂度：O(n 2 )

算法稳定性：稳定?

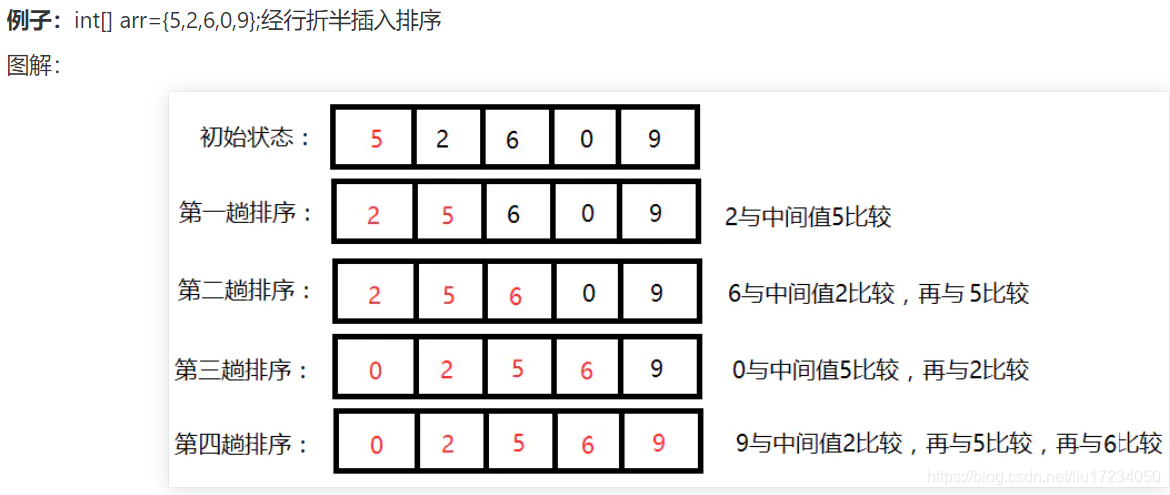
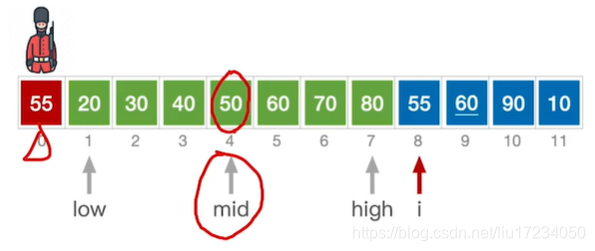
2.折半插入排序

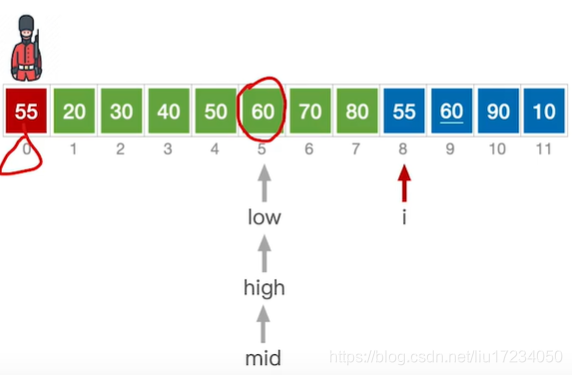
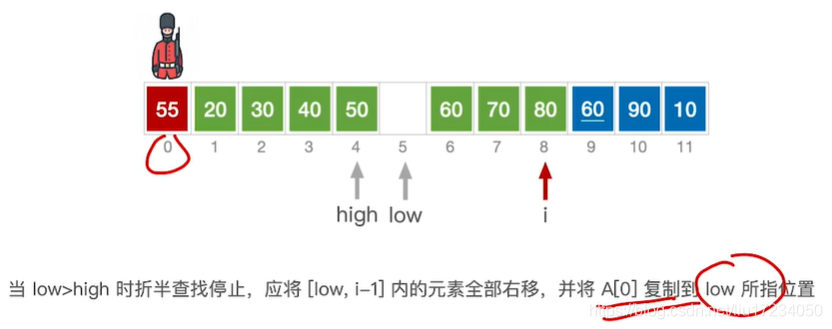
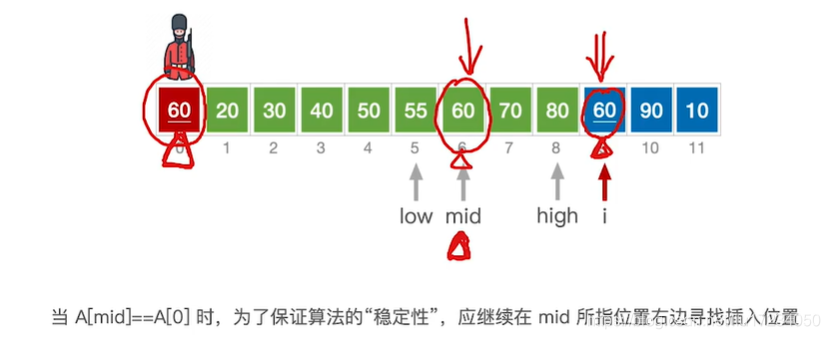
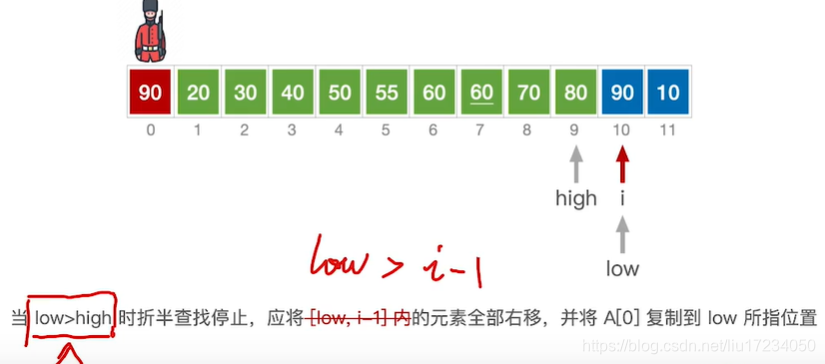
在直接插入排序的基础上，寻找插入位置时使用折半查找的方法?，适用于顺序表

//折半插入排序
    void InsertSort(int A[],int n){
        int i,j,low, high,mid;
        for( i=2 ; i<=n; i++){        //依次将A[2]~A[n]插入前面的已排序序列
            A[0]=A[i];                //将A[i]暂存到A[0]
            low=1;high=i-1;           //设置折半查找的范围
            while( low<=high){        //折半查找(默认递增有序)
                mid=( low+high)/2;    //取中间点
                if(A[mid]>A[0] ) 
                    high=mid-1; //查找左半子表else low=mid+1;l/查找右半子表
            }
            for(j=i-1; j>=high+1;--j)
                    A[j+1]=A[j];    //统一后移元素，空出插入位置
            A[high+1]=A[0];         //插入操作
        }
}

void BinaryInsertSort(int R[],int n) {
    int i, j, low, mid, high, temp;
    for(i = 1; i < n; i++) {
        low = 0;
        high = i - 1;
        temp = R[i];
        while(low <= high) {//找到合适的插入位置high+1，如果中间位置元素比要插入元素大，则查找区域向低半区移动，否则向高半区移动
            mid = (low + high) / 2;
            if(R[mid] > temp)
                high = mid - 1;
            else
                low = mid + 1;
        }
        for(j = i-1; j >= high+1; j--) {//high+1后的元素后移
            R[j+1] = R[j];
        }
        R[j+1] = temp;    //将元素插入到指定位置
    }
}

void BinaryInsertSort(int *a) {
    int i, low, high, mid;
    for (i = 1; i < 10; ++i) {
        low = 0, high = i - 1;
        while (low <= high) {　//折半查找
            mid = (low + high) / 2;
            if (a[i] < a[mid]) high = mid - 1;
            else low = mid + 1;
        }
        int temp = a[i];
        for (int k = i - 1; k >= low; --k) {
            a[k + 1] = a[k];
        }
        a[low] = temp;
    }


}


int main() {
    int a[10] = {0, -1, 2, -3, 4, -5, 6, -7, 8, -9};
    BinaryInsertSort(a);
    for (int i = 0; i < 10; ++i) {
        cout << a[i] << " ";
    }

    return 0;
}

最坏情况（整个序列逆序时）时间复杂度为O(n2)

最优情况（整个序列初始顺序，从大到小时）时间复杂度为O(nlog2n)

平均情况时间复杂度为O(n2)

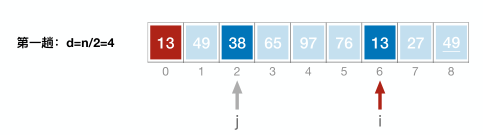
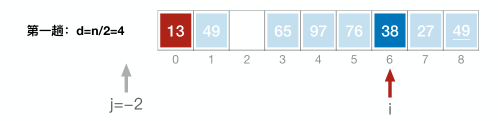
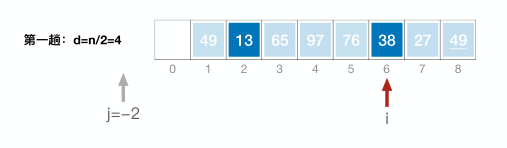
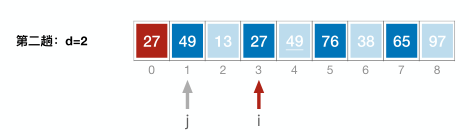
3.希尔排序【常考比较难】

点我跳转? ? ? ? 10：10

以d为增量序列，将原始序列划分成多个子表，各个子表内部使用直接插入排序；

然后再逐步减小d（一般可除以2），重复以上过程，直到d小于等于0

//希尔排序
void ShellSort(int A[] ,int n){
    int d, i，j;
        //A[0]只是暂存单元，不是哨兵，当j<=0时，插入位置已到
    for(d= n/2; d>=1; d=d/2)    //步长变化
        for( i=d+1; i<=n; ++i)
            if(A[i]<A[i-d] ){    //需将A[i]插入有序增量子表
                A[0]=A[i];       //暂存在A[0]
                for(j= i-d; j>0 && A[0]<A[j]; j-=d)
                        A[j+d]=A[j ];    //记录后移，查找插入的位置
                A[j+d]=A[0];             //插入
            }
}

void ShellSort(int a[], int n) {
    for (int div = n/2; div >= 1; div /= 2) {//步长变化
        for (int i = div + 1; i <= n; i++) {  
            for (int j = i; a[j] < a[j - div] && j >= 1; j -= div) {  
                swap(a[j], a[j-div]);  
            }  
        }  
    }
}

void shellSort(int a[], int n) {//对a[1]~a[n]进行排序
    int d, i, j;
    for (d = n / 2; d >= 1; d /= 2) {//d依次除以2
        for (i = d + 1; i <= n; ++i) {
            if (a[i] < a[i - d]) {
                a[0] = a[i];//a[0]作为暂存单元
                for (j = i - d; j >= 1 && a[0] < a[j]; j -= d) { //直接插入排序，后移操作
                    a[j + d] = a[j];
                }
                a[j + d] = a[0];
            }
        }
    }
}

int main() {
    int a[10] = {0, -1, 2, -3, 4, -5, 6, -7, 8, -9};
    shellSort(a, 9);
    for (int i = 1; i < 10; ++i) {
        cout << a[i] << " ";
    }

    return 0;
}

二：交换排序

1.冒泡排序

1.比较相邻的元素，如果前一个比后一个大，就把它们两个对调位置。

2.对排序数组中每一对相邻元素做同样的工作，直到全部完成，此时最后的元素将会是本轮排序中最大的数。

3.对剩下的元素继续重复以上的步骤，直到没有任何一个元素需要比较。

? 在这里插入图片描述

?每一趟可将当前剩余元素中的最大值或最小值放到确定的位置。共进行n-1趟。可设置一个标志flag进行优化

#include <iostream>

using namespace std;

void BubbleSort(int *a) {
    for (int i = 1; i < 10; ++i) { //共进行n-1趟排序
        bool flag = false;//标记位优化，如果某趟排序中未移动元素，说明已有序
        for (int j = 0; j < 10 - i; ++j) {
            if (a[j] > a[j + 1]) { //相邻两个元素之间进行比较
                int temp = a[j];
                a[j] = a[j + 1];
                a[j + 1] = temp;
                flag = true;
            }
        }
        if (flag == false)
            return;
    }
}

int main() {
    int a[] = {9, 8, 7, 6, 5, 4, 3, 2, 1, 0};
    BubbleSort(a);
    for (int i = 0; i < 10; ++i) {
        cout << a[i] << " ";
    }
    return 0;
}

void Swap(int arr[], int i, int j)
{
    int temp=arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}

/**
* 冒泡排序
* 最差时间复杂度 O(n^2)
* 最优时间复杂度 O(n)
* 平均时间复杂度 O(n^2)
* 空间复杂度    O(1)
* 稳定性       稳定
* 效率         对于少数元素之外的数列排序是很没有效率的
* @param arr 数组
* @param n 长度
*/
void BubbleSort(int arr[], int n) {
    for (int i=0;i<n-1;i++)//每次最大元素就像气泡一样浮到数组的最后
    {
        for(int j=0;j<n-1-i;j++) //依次比较相邻的两个元素，使较大的那个向后移
        {
            if(arr[j]>arr[j+1]) //如果条件改为arr[j] >= arr[j+1] 则变为不稳定的排序算法
            {
                Swap(arr, j, j + 1);
            }
        }
    }
}

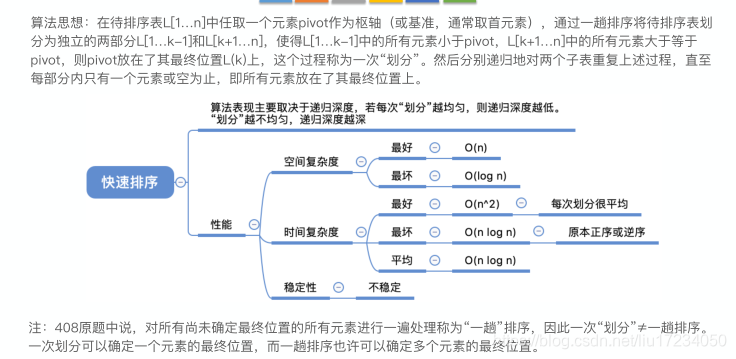
?2.快速排序【常考】

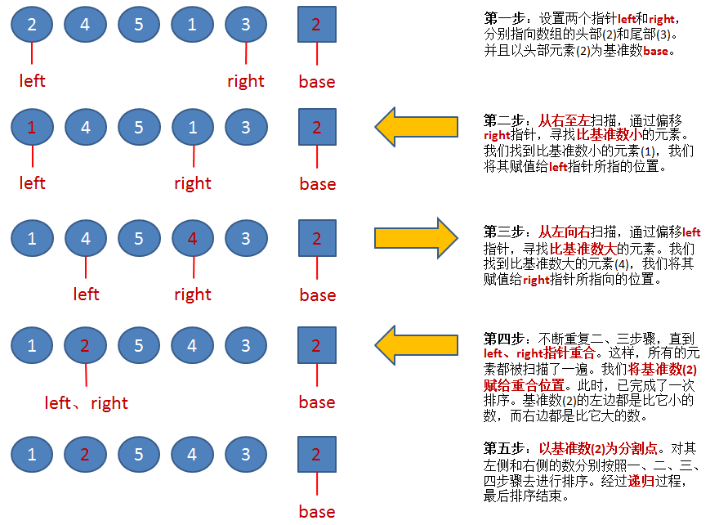
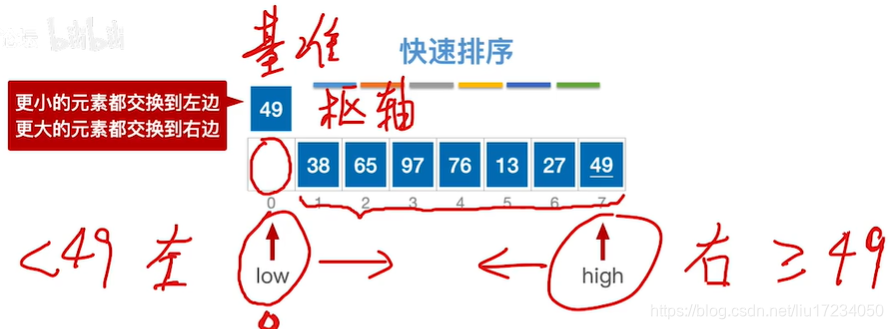
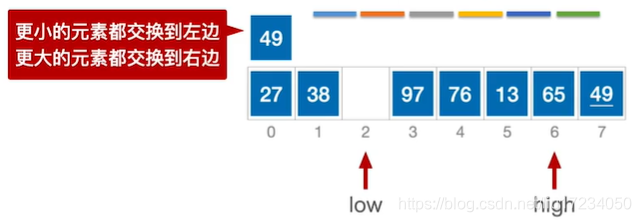
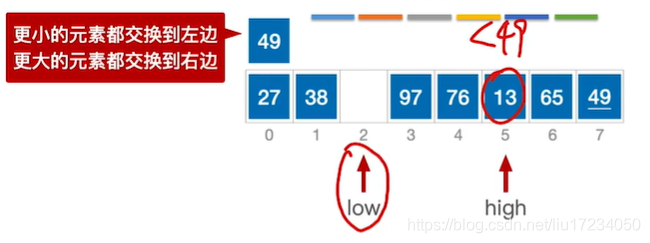
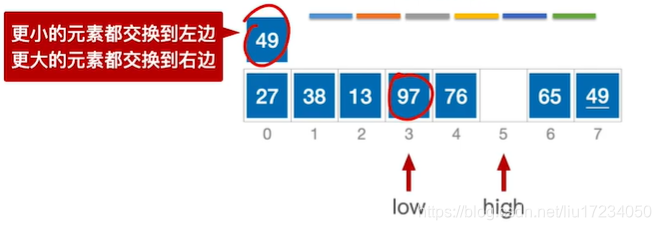
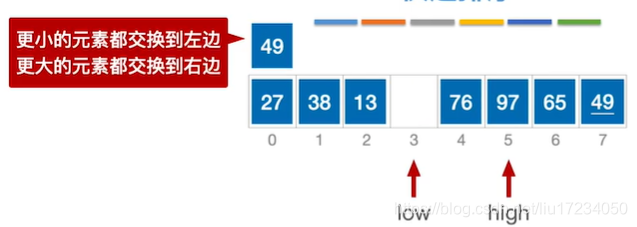
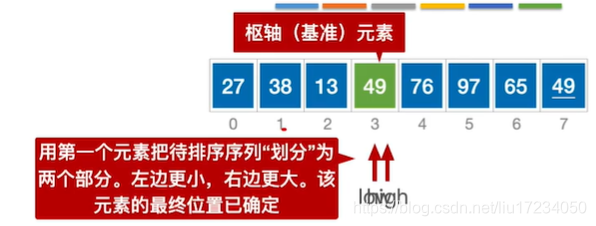
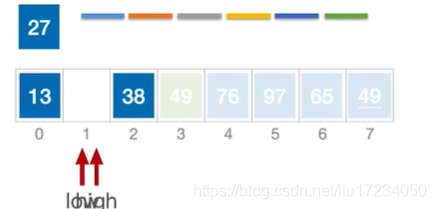
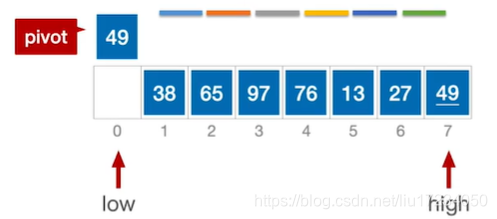
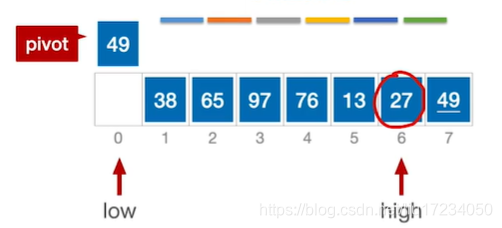
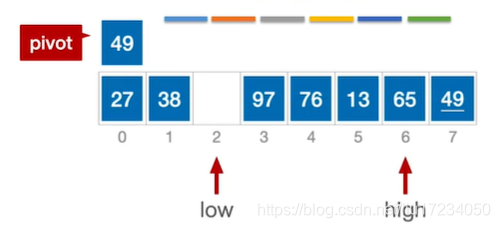
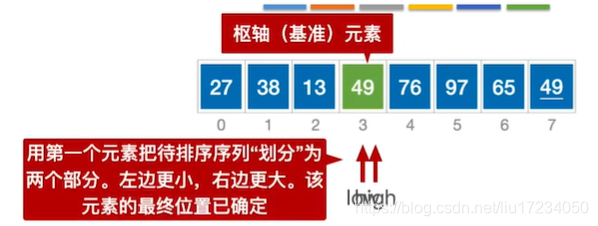
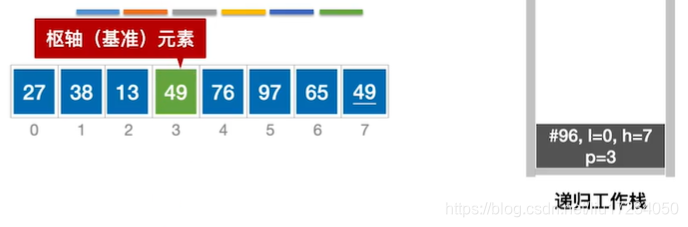
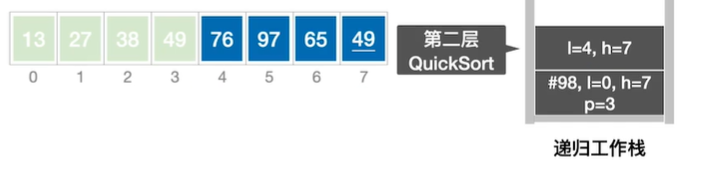
通过一趟排序将要排序的数据分割成独立的两部分：分割点左边都是比它小的数，右边都是比它大的数。

然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列

low作为基准元素；哪个为空另外一个就移动

-------------------------------------------------------------------------------------------------------------------------------------

#include <iostream>

using namespace std;
const int LENGTH = 10;

//用第一个元素将待排序序列划分为左右两个部分
int Partiton(int a[], int low, int high) { //划分
    int temp = a[low];      //第一个元素作为一个枢轴
    while (low < high) {    //low和high搜索枢轴的最终位置
        while (low < high && a[high] >= temp) high--;
        a[low] = a[high];   //比较枢轴小的元素移动到左端
        while (low < high && a[low] <= temp) low++;
        a[high] = a[low];   //比较枢轴大的元素移动到右端
    }
    a[low] = temp;    //枢轴元素存放在最终位置
    return low;       //返回存放枢轴的最终位置
}

void QuickSort(int a[], int low, int high) { //排序
    if (low < high) {    //递归跳出的条件
        int pivot = Partiton(a, low, high);
        QuickSort(a, low, pivot - 1);    //划分左子表
        QuickSort(a, pivot + 1, high);   //划分右子表
    }
}

int main() {
   int a[LENGTH] = {2, 5, 1, 1, 10, 6, 2, 4, 3, 5};
    cout << "初始序列：";
    for (int i = 0; i < LENGTH; ++i) {
        cout << a[i] << " ";
    }
    cout << endl;
    cout << "排序之后：";
    QuickSort(a, 0, LENGTH - 1);
    for (int i = 0; i < LENGTH; ++i) {
        cout << a[i] << " ";
    }
    return 0;
}

#include <stdio.h>
int a[1005];  
//快速排序
void Quick_Sort(int l, int r) {
    if(l >= r) return;
    int i = l;
    int j = r;
    int x = a[l];
    while (i < j) {
        while (i < j && a[j] >= x) j--;
        if (i < j) a[i++] = a[j];
        while (i < j && a[i] < x) i++;
        if (i < j) a[j--] = a[i];
    }
    a[i] = x;
    Quick_Sort(l, i - 1);//比i小的继续划分
    Quick_Sort(i + 1, r);//比i大的继续划分
}
  
int main() {  
    int n;  
    scanf("%d", &n);//输入n个数进行快速排序
    for (int i = 1; i <= n; i++) scanf("%d", &a[i]);  
    Quick_Sort(1, n);
    for (int i = 1; i <= n; i++) {
        printf("%d ", a[i]);  
    }  
    printf("\n");  
    return 0;  
}

三：选择排序

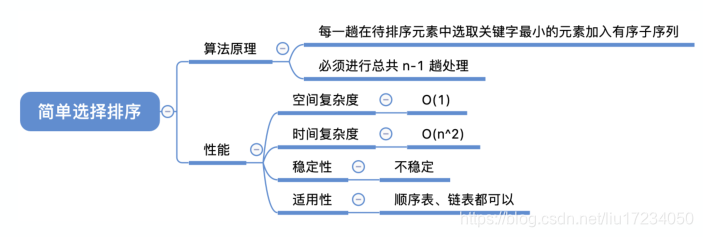
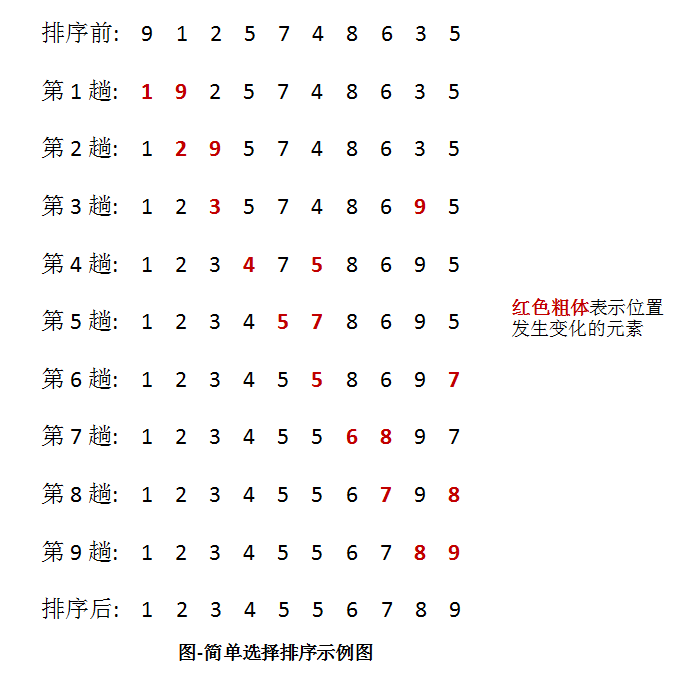
1.简单选择排序

从待排序序列中，找到关键字最小的元素；
如果最小元素不是待排序序列的第一个元素，将其和第一个元素互换；
从余下的 N - 1 个元素中，找出关键字最小的元素，重复(1)、(2)步，直到排序结束。

排序（5）：简单选择排序

void SelectSort(ElemType A[], int n) {
    for (int i = 0; i < n - 1; i++) {//一共进行n-1趟
        int min_p = i;//记录最小元素位置
        for (int j = i + 1; j < n; j++)//在A[i...n-1]中选择最小的元素
            if (A[i] < A[min_p]) min_p = j;//更新最小元素位置
        if (min_p != i) swap(A[i], A[min_p]);//封装的swap()函数共移动元素3次
    }
}

#include <iostream>

using namespace std;

void SelectSort(int *a,int n) {


    for (int i = 0; i < n-1; ++i) { //n-1趟排序
        int index = i;
        for (int j = i + 1; j < n-1; ++j) { //找到a[index]应插入的位置
            if (a[j] < a[index])
                index = j;
        }
        if (i != index) {//交换元素
            int temp = a[i];
            a[i] = a[index];
            a[index] = temp;
        }

    }
}

int main() {
    int a[] = {0, 5, -1, 3, 2, 4, 9, 8, 7, 6};
    SelectSort(a,10);
    for (int i = 0; i < 10; ++i) {
        cout << a[i] << " ";
    }
    return 0;
}

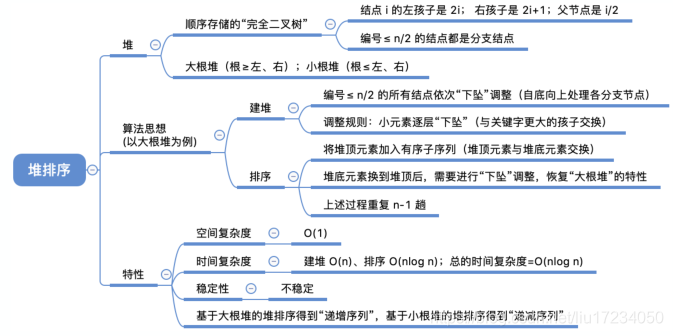
2.堆排序【常考】

堆排序是利用堆的性质进行的一种选择排序

排序（6）：堆排序

堆是一棵顺序存储的完全二叉树?

其中每个结点的关键字都不大于其孩子结点的关键字，这样的堆称为小根堆。
其中每个结点的关键字都不小于其孩子结点的关键字，这样的堆称为大根堆。

（1）根据初始数组去构造初始堆（构建一个完全二叉树，保证所有的父结点都比它的孩子结点数值大）。

（2）每次交换第一个和最后一个元素，输出最后一个元素（最大值），然后把剩下元素重新调整为大根堆。

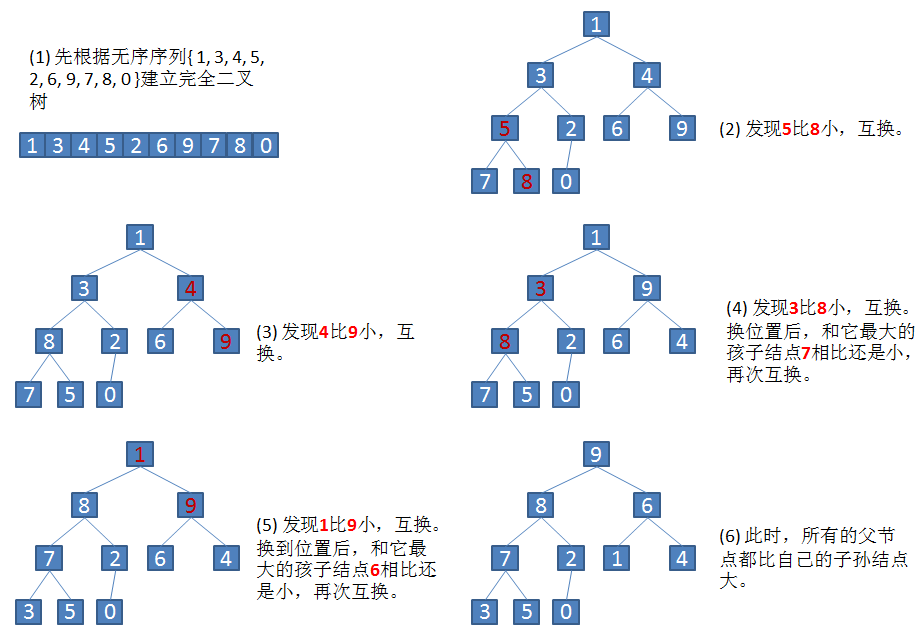
2.1 构建创建初始堆

?设有一个无序序列 { 1, 3, 4, 5, 2, 6, 9, 7, 8, 0 }

?2.2 堆排序处理

?

?2.3 代码实现

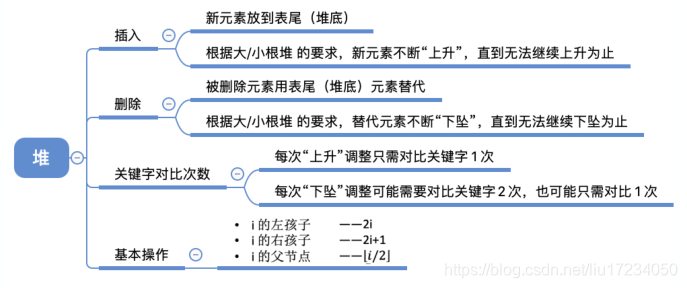
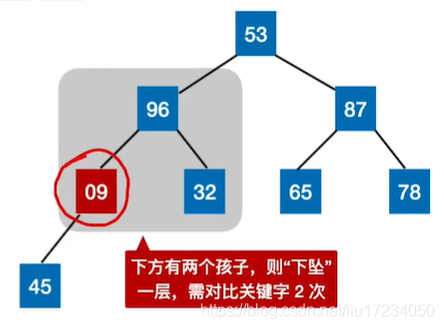
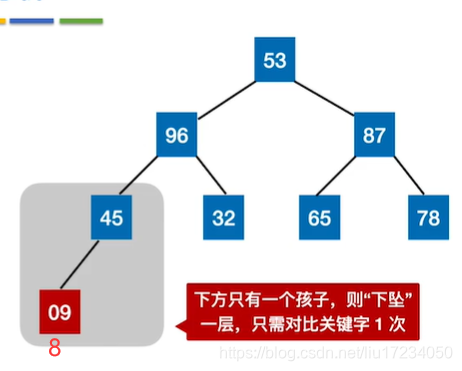
结论：?个结点，每“下坠”?层，最多只需对?关键字2次
若树?为h，某结点在第 i 层，则将这个结点向下调整最多只需要“下坠” h-i 层，关键字对?次数不超过 2(h-i)

注意：若左右孩??样?，则优先和左孩?交换

//将以k 为根的子树调整为大根堆
void HeadAdjust(int A[ ],int k,int len){
    A[O]=A[k];                       //A[0]暂存子树的根结点
    for(int i=2*k ; i<=len;i*=2){    //沿key较大的子结点向下筛选
        if( i<len&&A[i]<A[i+1])      //看左右孩子谁更大
            i++;                     //取key较大的子结点的下标
        if(A[0]>=A[i])               //根节点和最大的孩子结点比较
                break;               //筛选结束
        else{
                A[k]=A[i];           //将A[i]调整到双亲结点上
                k=i;                 //修改k值,以便继续向下筛选
            }
    }
    A[k]=A[0];                        //被筛选结点的值放入最终位置
}

#include <iostream>
using namespace std;
//调整堆
void HeapAdjust(int *a, int i, int n) {
    int lc = i << 1;
    int rc = (i << 1) + 1;
    int max = i;
    if (i > n / 2) return;
    if (lc <= n && a[lc] < a[max]) max = lc;
    if (rc <= n && a[rc] < a[max]) max = rc;
    if(max != i) {
        swap(a[i], a[max]);
        HeapAdjust(a, max, n);
    }
}
//创建堆
void BuildHeap(int *a, int n) {
    for (int i = n / 2; i >= 1; i--) {//从前往后调整所有非终端结点
        HeapAdjust(a, i, n);
    }
}
//堆排序
void HeapSort(int *a, int n) {
    BuildHeap(a, n);                  //初始建堆
    for (int i = n; i >= 1; i--) {    //n-1趟的交换和建堆过程
        swap(a[1], a[i]);             //堆顶元素和堆底元素交换
        HeapAdjust(a, 1, i - 1);      //把剩余的待排序元素整理成堆
    }
}
int main() {
    int n;
    int a[1005];
    scanf("%d", &n);//输入n个数，堆排序输出
    for (int i = 1; i <= n; i++) scanf("%d", &a[i]);
    HeapSort(a, n);
    for (int i = 1; i <= n; i++) {
        printf("%d ", a[i]);
    }
    printf("\n");
    return 0;
}

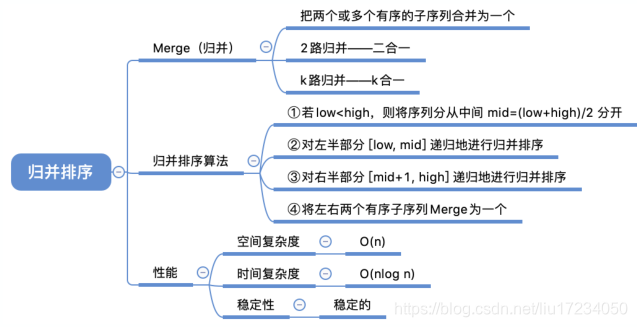
四：归并排序（二路归并）

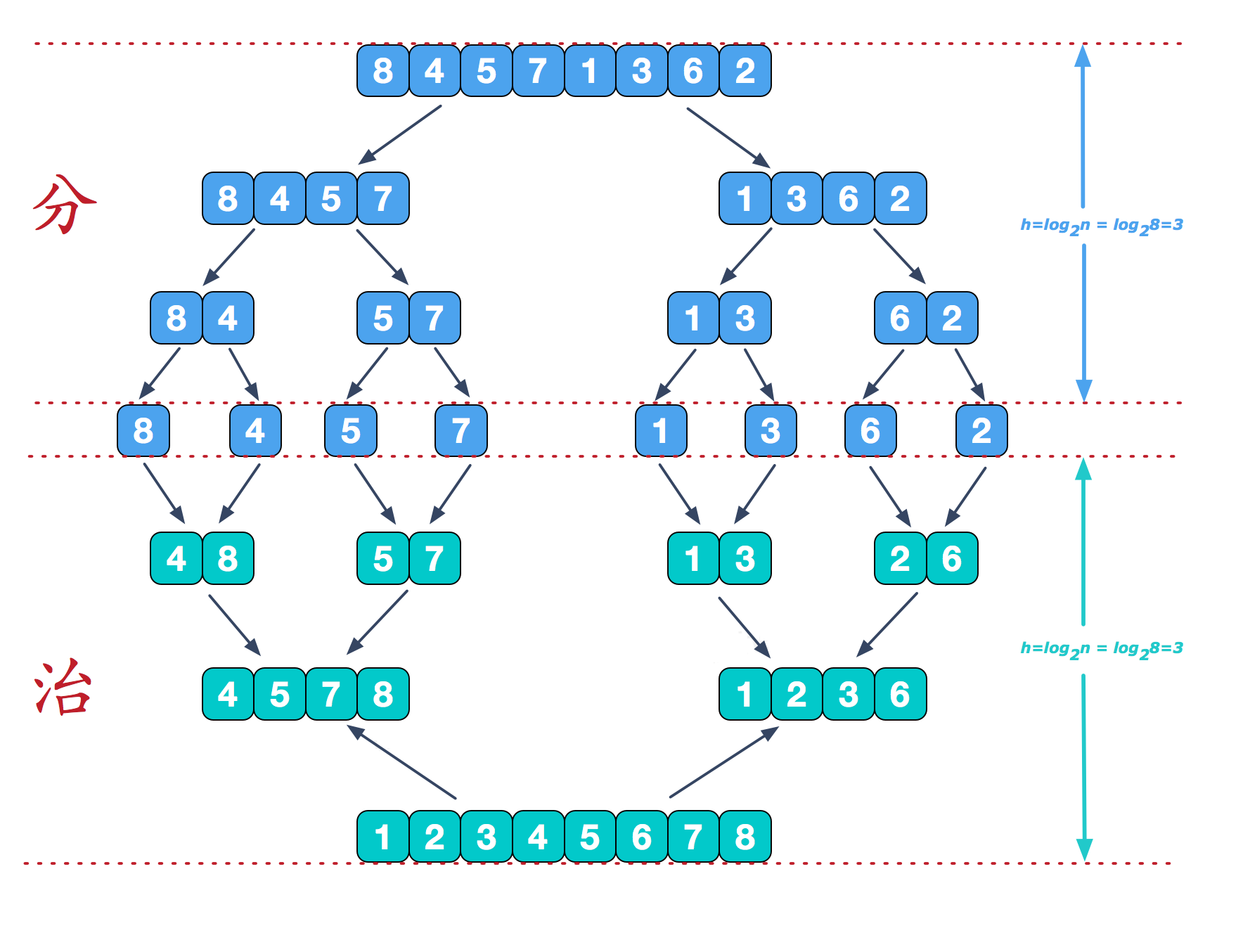
分而治之：分阶段；治阶段?

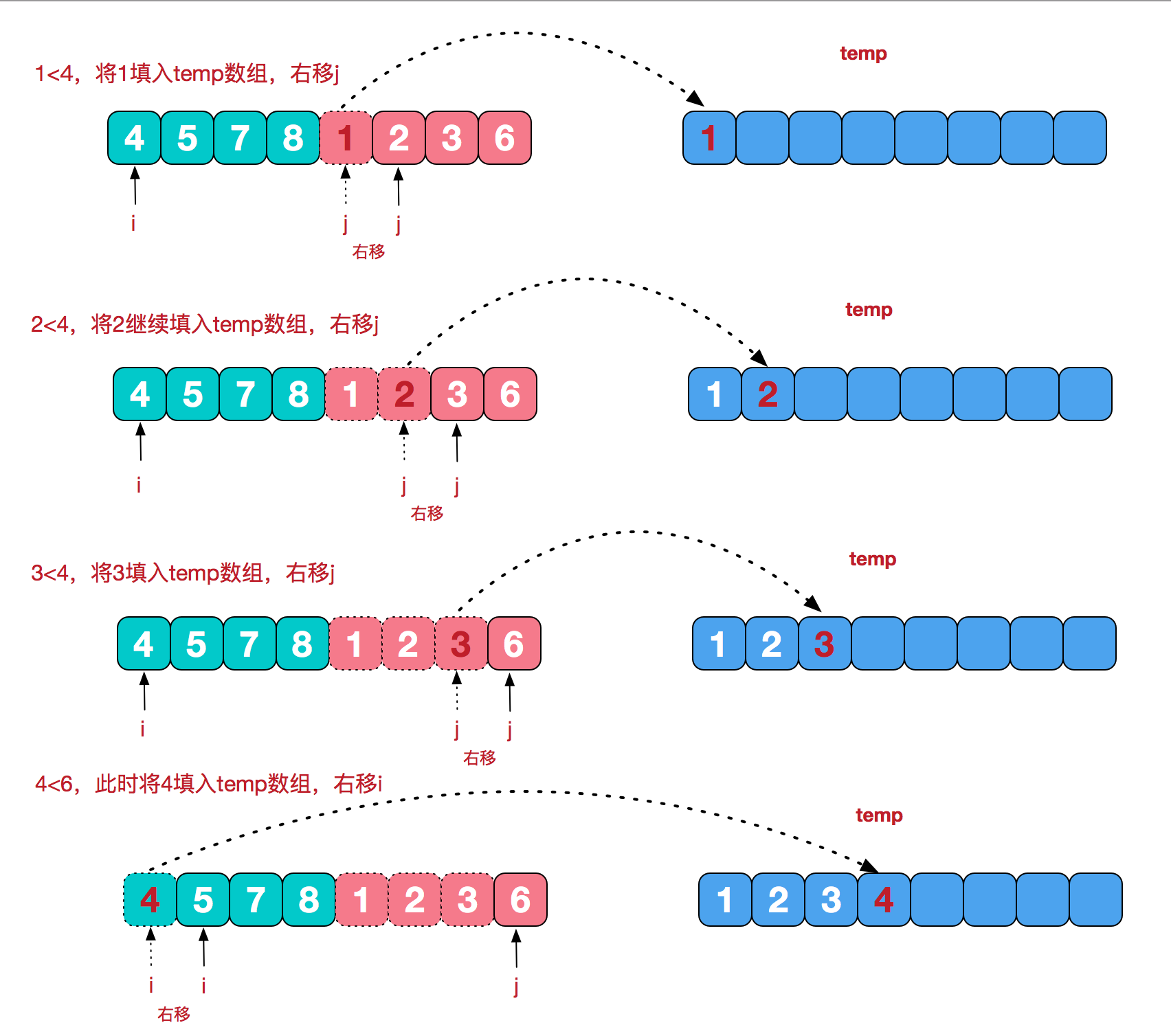
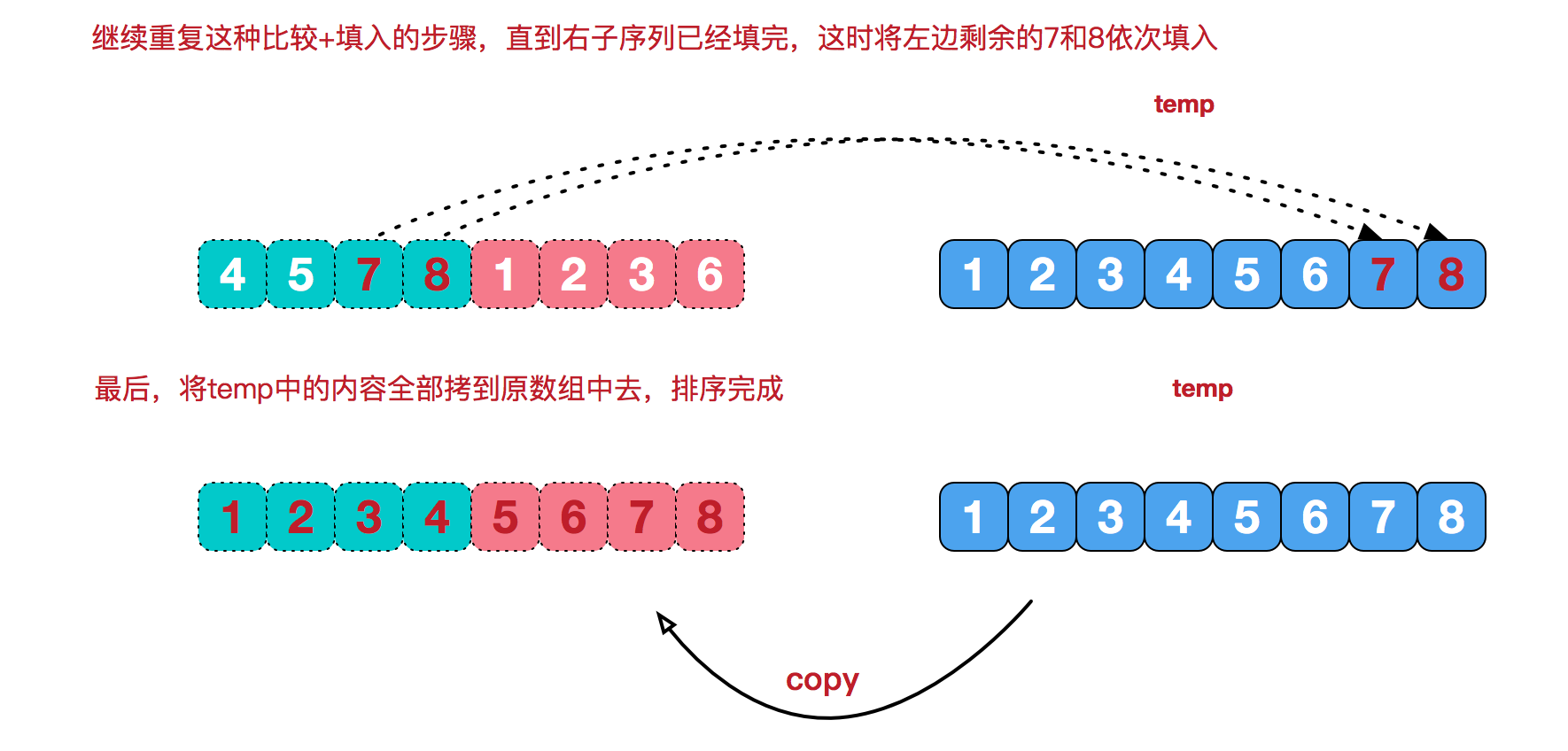
将初始长度为n序列，一分为二

    对得到的左边子序列继续二分，依次类推
        直到最后左边的子序列划分所得两个子序列各包含一个元素

    然后再将其两两归并，得到一个有序的子序列

    然后再按照同样的策略继续划分右边的子序列，然后归并……直到最终归并为长度为n的有序子序列

排序（7）：归并排序

? 排序（7）：归并排序

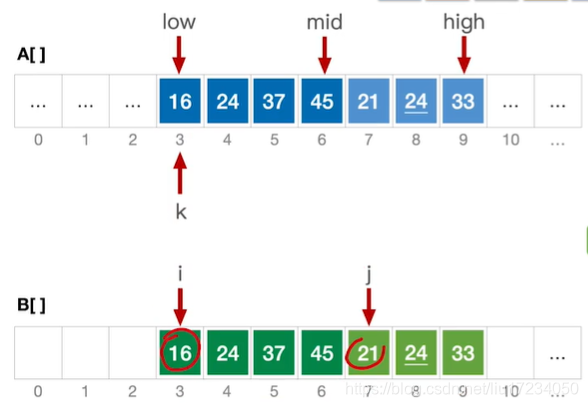
int *B=(int *)malloc( n*sizeof(int));    //辅助数组B

//A[ low...mid]和A[mid+...high]各自有序，将两个部分归并
void Merge(int A[],int low,int mid,int high)
{
    int i,j,k;
    for( k=low ; k<=high;k++)
        B[k]=A[k];    //将A中所有元素复制到B中
    for( i=low , j=mid+1,k=i; i<=mid&&j<=high ;k++)    //归并
    {
        if(B[i]<=B[j])
            A[k]=B[i++];    //将较小值复制到A中
        else
            A[k]=B[j++];
    }
    while( i<=mid)A[k++]=B[i++];
    while(j<=high)A[k++]=B[j++];
}



void MergeSort(int A[] ,int low,int high)
{
    if (low<high)
    {
        int mid=(low+high)/2;    //从中间划分
        MergeSort(A,low,mid);    //对左半部分归并排序
        MergeSort(A,mid+1,high); //对右半部分归并排序
        Merge(A,low,mid,high);   //归并
    }
}

#include <stdio.h>
#define MAX 1000001

int a[MAX], b[MAX];
//将两段有序的区间合并为一段，复杂度为线性
void Merge(int a[], int low, int mid, int high) {
    int i = low, j=mid+1, k = low;
    while(i!=mid+1 && j!=high+1) {
        if(a[i] >= a[j])
            b[k++] = a[j++];
        else
            b[k++] = a[i++];
    }
    while(i != mid+1)
        b[k++] = a[i++];
    while(j != high+1)
        b[k++] = a[j++];
    for(i=low; i<=high; i++)
        a[i] = b[i];
}
//归并排序
void MergeSort(int a[], int low, int high) {
    int mid;
    if(low < high) {
        mid = (low + high) / 2;
        MergeSort(a, low, mid);//前面部分
        MergeSort(a, mid+1, high);//后面的部分
        Merge(a, low, mid, high);//合并
    }
}
int main() {
    int i, n;
    scanf("%d",&n);
    for(i=0; i<n; i++) scanf("%d",&a[i]);
    MergeSort(a, 0, n-1);
    for(i=0; i<n; i++)
        printf("%d ", a[i]);
    printf("\n");
    return 0;
}

五：基数排序

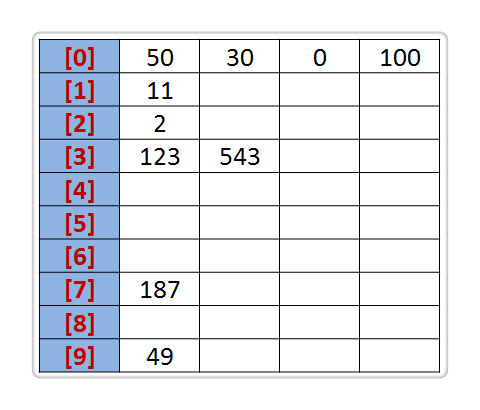
将所有待比较数值（正整数）统一为同样的数位长度，数位较短的数前面补零。
从最低位开始，依次进行一次排序。
这样从最低位排序一直到最高位排序完成以后, 数列就变成一个有序序列
设有一个初始序列为: R {50, 123, 543, 187, 49, 30, 0, 2, 11, 100}

以 0~9 来表示的，所以我们不妨把 0~9 视为 10 个桶

第一步：先根据序列的个位数的数字来进行分类，将其分到指定的桶中?

第二步：从各个桶中，将这些数按照从编号 0 到编号 9 的顺序依次将所有数取出来，得到的序列就是个位数上呈递增趋势的序列

????????????????按照个位数排序： {50, 30, 0, 100, 11, 2, 123, 543, 187, 49}

第三步：接下来，可以对十位数、百位数也按照这种方法进行排序，最后就能得到排序完成的序列
#include <bits/stdc++.h>
using namespace std;

const int maxn = 1005;
int a[maxn];
/*思想：基数排序其实就是按位排序、实现时用分桶的方法
可以从低位到高位、也可以从高位到低位*/
void Radix_Sort(int n, int k) {
    vector<int> v[10];//10个位对应10个桶
    int radix = pow(10, k);
    int flag = 1;
    for (int i = 1; i <= n; i++) {
        if (a[i] >= radix) flag = 0;
        int w = (a[i] % radix) / (radix / 10);
        v[w].push_back(a[i]);
    }
    int cnt = 1;
    for (int i = 0; i <= 9; i++) {//从低到高枚举每个位
        for (int j = 0; j < v[i].size(); j++) {
            a[cnt++] = v[i][j];
        }
    }
    if (flag) return;
    Radix_Sort(n, k + 1);
}

int main() {
    int n;
    scanf("%d", &n);//输入n个数用基数排序进行排序
    for (int i = 1; i <= n; i++) {
        scanf("%d", &a[i]);
    }
    Radix_Sort(n, 1);
    for (int i = 1; i <= n; i++) {
        printf("%d ", a[i]);
    }
    printf("\n");
    return 0;
}

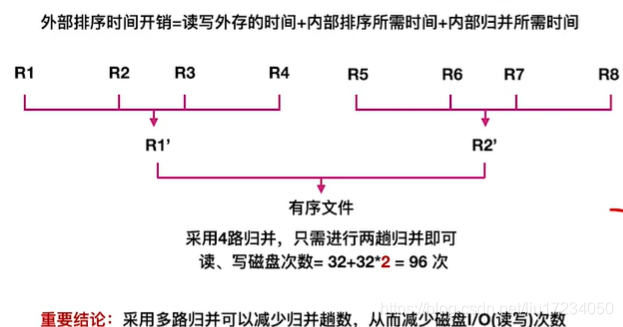
?六：外部排序——多路归并排序

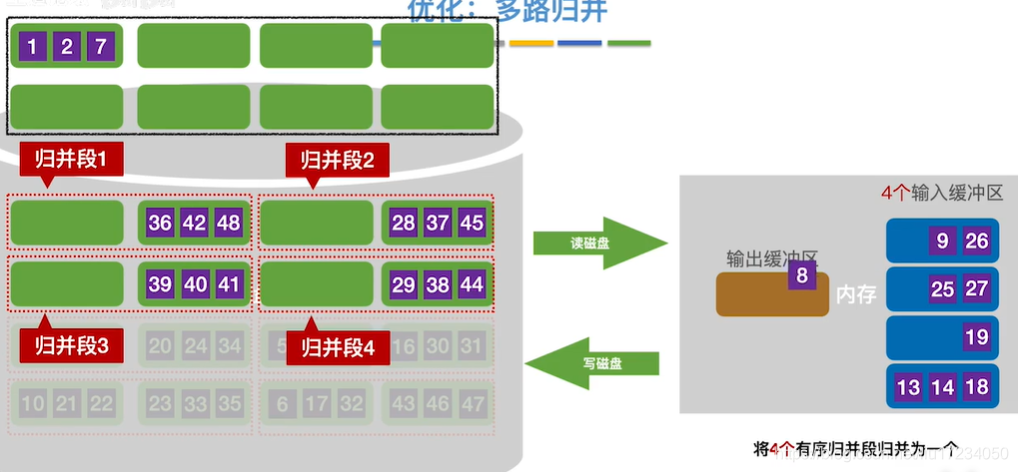
1.多路归并?

其直接影响算法效率的因素为读写外存的次数，即次数越多，算法效率越低



若想提高算法的效率，即减少算法运行过程中读写外存的次数，可以增加 k –路平衡归并中的 k 值

但是经过计算得知，如果毫无限度地增加 k 值，虽然会减少读写外存数据的次数，但会增加内部归并的时间，得不偿失
为了避免在增加 k 值的过程中影响内部归并的效率，在进行 k-路归并时可以使用“败者树”来实现

该方法在增加 k 值时不会影响其内部归并的效率

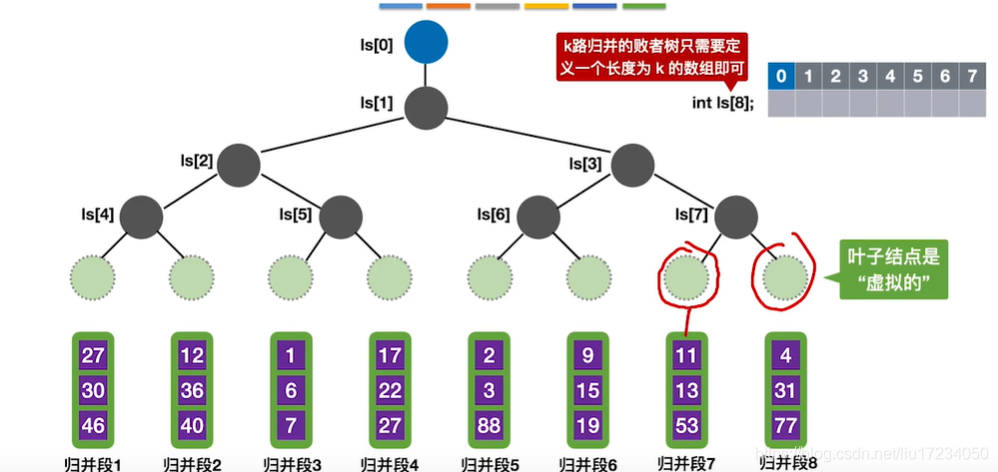
2.败者树实现内部归并

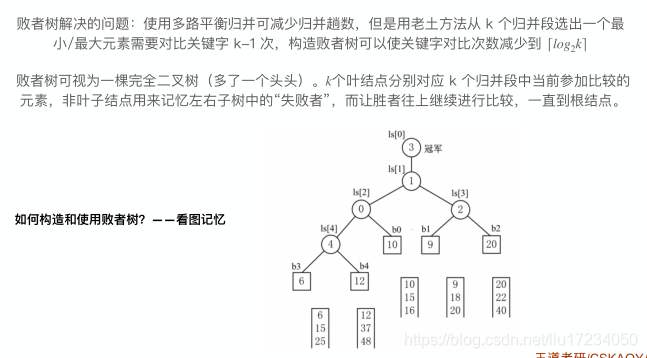
败者树是树形选择排序的一种变形，本身是一棵完全二叉树

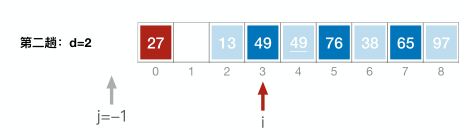
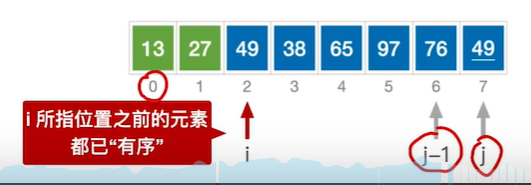
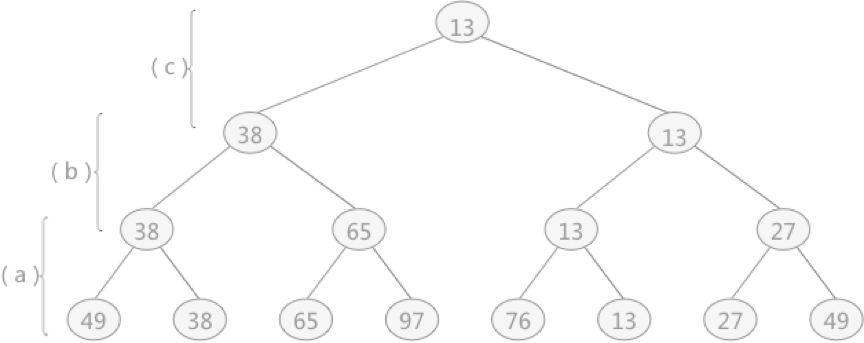
于无序表{49，38，65，97，76，13，27，49}创建的完全二叉树如图 1 所示，构建此树的目的是选出无序表中的最小值

是一棵“胜者树”

因为树中每个非终端结点（除叶子结点之外的其它结点）中的值都表示的是左右孩子相比较后的较小值（谁最小即为胜者）?
而败者树恰好相反，其双亲结点存储的是左右孩子比较之后的失败者，而胜利者则继续同其它的胜者去比较
胜者树和败者树的区别就是：
    胜者树中的非终端结点中存储的是胜利的一方

    而败者树中的非终端结点存储的是失败的一方
?

?

?在多路平衡归并的时候，引入败者树，可以减少归并趟数

3.置换选择排序

?

?

?

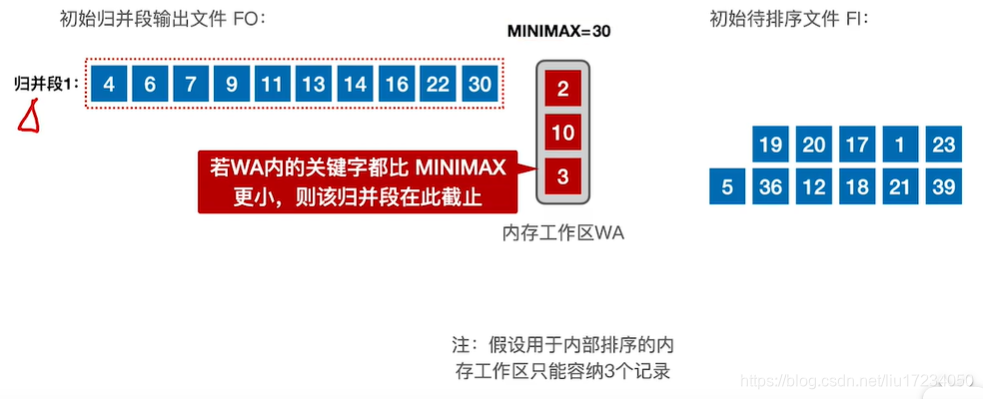
初始归并段的长度可以超过内存工作区的长度限制（本来是3个，限制内存归并段超过了3个）

归并段包含的纪录越多，那么归并段的总数就会越小r

那么进行外部排序，读写磁盘的次数也会越少

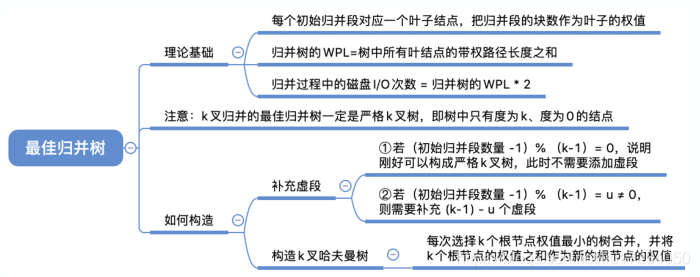
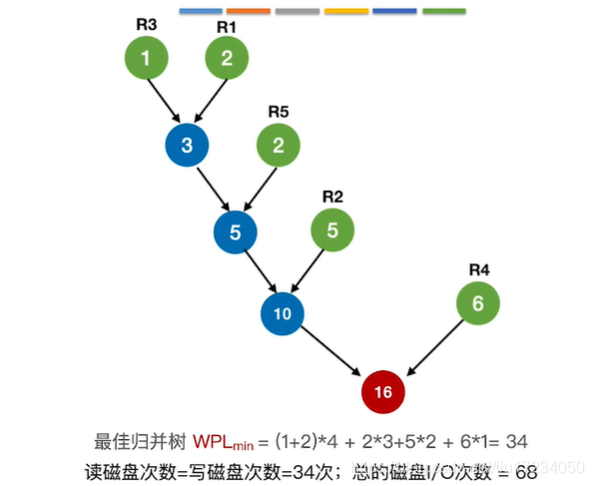
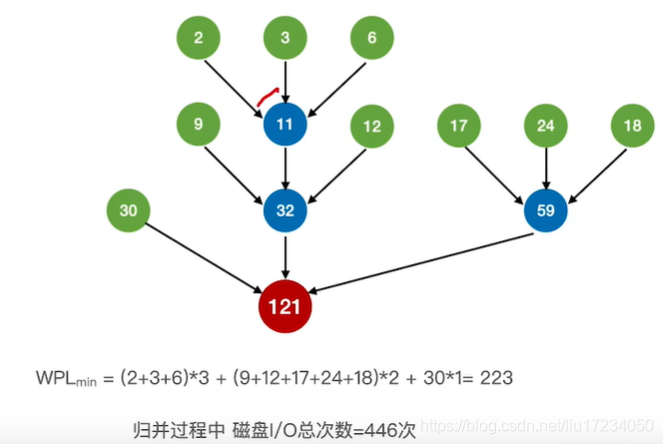
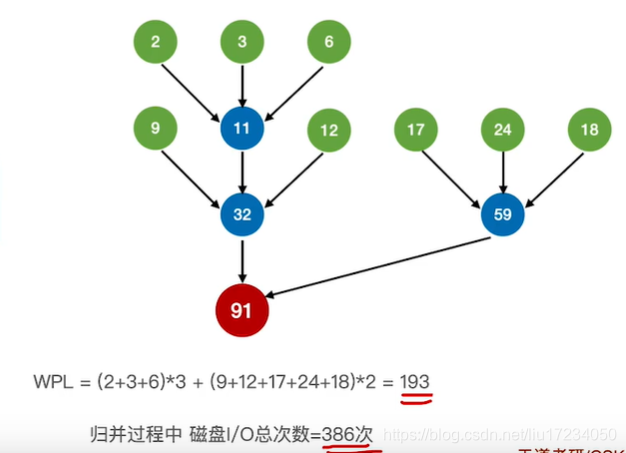
4.最佳归并树

?

?

?????????????????????????????????之前的????????????????????????????????????????????????????????????????????????????????????????????????现在的?

?

?????????????????????????????????不够的情况? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 增加虚段?

?

?初始归并段：个数? ? ? ? K：几路归并

?