一、题目

给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中，返回 true ；否则，返回 false 。

单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。
例如，在下面的 3×4 的矩阵中包含单词 “ABCCED”（单词中的字母已标出）。
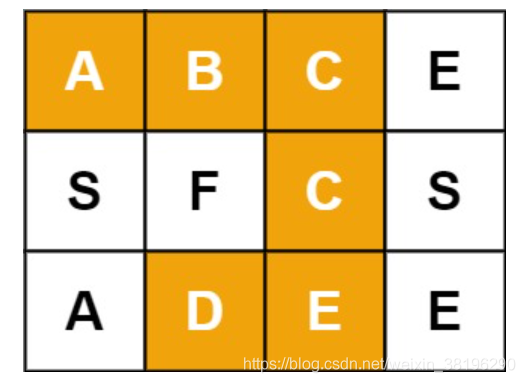
在这里插入图片描述

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/ju-zhen-zhong-de-lu-jing-lcof
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

二、回溯法

2.1 回溯法模板

  '''
        void backtracking(参数) {
            if (终止条件) {
                存放结果;
                return;
            }

            for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
                处理节点;
                backtracking(路径，选择列表); // 递归
                回溯，撤销处理结果
            }
        }
        '''

引用自公众号：代码随想录 https://mp.weixin.qq.com/s/ko0zLJplF7n_4TysnPOa_w

2.2 思路

（1）中止条件

因为每个单元格都可以向其前后左右四个方向前进，也就是从 $b o a r d [i] [j]$ 可以走到 $b o a r d [i + 1] [j]$ ， $b o a r d [i ? 1] [j]$ ， $b o a r d [i] [j + 1]$ ， $b o a r d [i] [j ? 1]$ ，需要考虑越界情况。
如果当前的 $b o a r d [i] [j]$ 和它需要匹配的 $w o r d [k]$ 不相等时，需要返回 False。
如果当前的word已经被全部匹配成功，也就是当前下标 $k = = l e n (w o r d) ? 1$
时，说明已将找到该word，返回 True。

（2）同一个单元格内的字母在同一次回溯中不允许被重复使用。

不能在一次回溯中从 $b o a r d [1] [0]$ —> $b o a r d [1] [1]$ —> $b o a r d [1] [0]$ 。
使用栈来理解：
栈中存放着当前已经和word[0]~word[k-1]的元素，下一个需要匹配的元素入栈，判断是否和word[k]匹配，如果匹配，继续遍历该元素的前后左右（必定有一个是自己，不能匹配，需要剪枝），知道返回True或者返回False。
如果返回False，当前栈顶元素出栈，下一个栈顶元素的其他方向元素入栈，进行判断。
因为不能重复处理，所以需要在当前元素入栈之后，将其置为空（处理结点），在出栈的时候重新赋原来的值，也就是当前 $w o r d [k]$ (回溯，撤销处理结果).

(3) 每一个单元格都可能是与word相匹配的首个单元格，所以需要在外面对其双层遍历，使每一个单元格，都与 $w o r d [0]$ 开始匹配，进而找到整个word。

2.3 具体代码

class Solution:
    def exist(self, board: List[List[str]], word: str) -> bool:
       #回溯法 ---- 在集合中递归查找子集

      
        #i为行坐标，j为列坐标，k为 word 的元素下标
        def backtracking(i,j,k):
            #越界
            if i<0 or i>=len(board) or j<0 or j>=len(board[0]):
                return False
            #如果值不相等
            if board[i][j]!=word[k]:
                return False
            
            #如果已将 word 匹配完成
            if k==len(word)-1:
                return True
            #栈中存放当前与word匹配的字符
            #未避免重复使用元素,已经入过栈的元素，将其赋值为空字符串
            board[i][j]=''
            #如果当前下标元素匹配成功，向前后左右四个方向继续匹配
            res=backtracking(i-1,j,k+1) or backtracking(i+1,j,k+1) or backtracking(i,j+1,k+1) or backtracking(i,j-1,k+1)
            #回溯，撤销结果
            board[i][j]=word[k]
            return res

        for i in range(len(board)):
            for j in range(len(board[0])):
                #每一个点都可能是与word相匹配的首个单元格
                if backtracking(i,j,0):
                    return True
        return False