树的存储结构
?树的存储方式有多种,既可以采用顺序存储结构,又可以采用链式存储结构,但无论何种存储方式,都要求能够唯一的反映树中各结点之间的逻辑关系。
?常用的存储结构主要有:
?<1> 双亲表示法
?<2> 孩子表示法
?<3> 孩子兄弟表示法
<1>双亲表示法
?采用一组连续空间来存储每个结点,同时在每个结点中增设一个伪指针,指示其双亲结点在数组中的位置。
?如下图所示,根结点的下标为0,其伪指针域为-1。
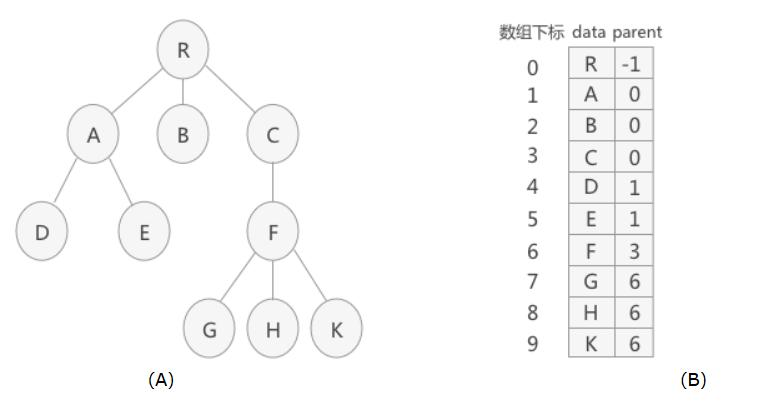
?这种双亲表示法的存储结构描述如下:
#define MaxSize 100 //树中最多结点数
typedef struct{ //树的结点定义
char data; //数据元素
int parent; //双亲位置域
}PTNode;
typedef struct{ //树的类型定义
PTNode nodes[MaxSize]; //双亲表示
int n; //结点数
}PTree;
?对于上图的完整代码实现如下:
#include<bits/stdc++.h>
using namespace std;
#define MaxSize 100 //树中最多的结点数
typedef struct{ //结点定义
char data; //数据
int parent; //双亲位置域
}PTNode;
typedef struct{
PTNode nodes[MaxSize]; //双亲表示,存放树中所有结点
int n; //结点数
}PTree;
//树的结点初始化
PTree InitPNode(PTree tree){
cout<<"请输入结点个数: ";
cin>>tree.n;
cout<<"请输入结点的值及其双亲位于数组中的位置下标:"<<endl;
char ch;
int j;
for(int i=0; i<tree.n; i++){
fflush(stdin); //清空输入缓冲区
cin>>ch>>j;
tree.nodes[i].data = ch; //结点数据
tree.nodes[i].parent = j; //双亲结点在数组中的位置
}
return tree;
}
//查找树中指定结点
void FindParent(PTree tree){
cout<<"请输入要查询的结点值:";
fflush(stdin); //清空输入缓冲区
char a;
cin>>a; //输入要查询的结点值
int flag = 0;
for(int i=0; i<tree.n; i++){
if(tree.nodes[i].data == a){
flag = 1;
if(i == 0){ //此时为根结点
cout<<"此结点为根结点!"<<endl;
break;
}
int ad = tree.nodes[i].parent;
cout<<a<<"的父结点为: "<<tree.nodes[ad].data<<endl;
cout<<"存储位置为: "<<ad<<endl;
break;
}
}
if(flag == 0){
cout<<"树中无此结点。"<<endl;
}
}
int main(){
PTree tree;
tree = InitPNode(tree);
FindParent(tree);
return 0;
}
?运行结果为:
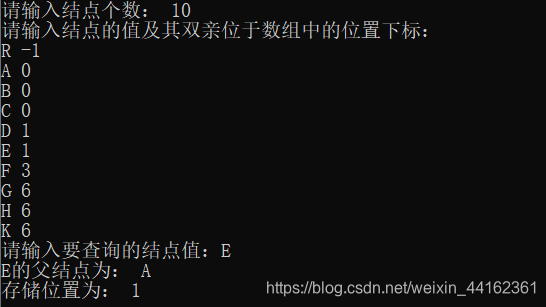
<2>孩子表示法
?将每个结点的孩子结点都用单链表链接起来形成一个线性结构,此时n个结点就有n个孩子链表(叶子结点的孩子链表为空表),如下图所示。
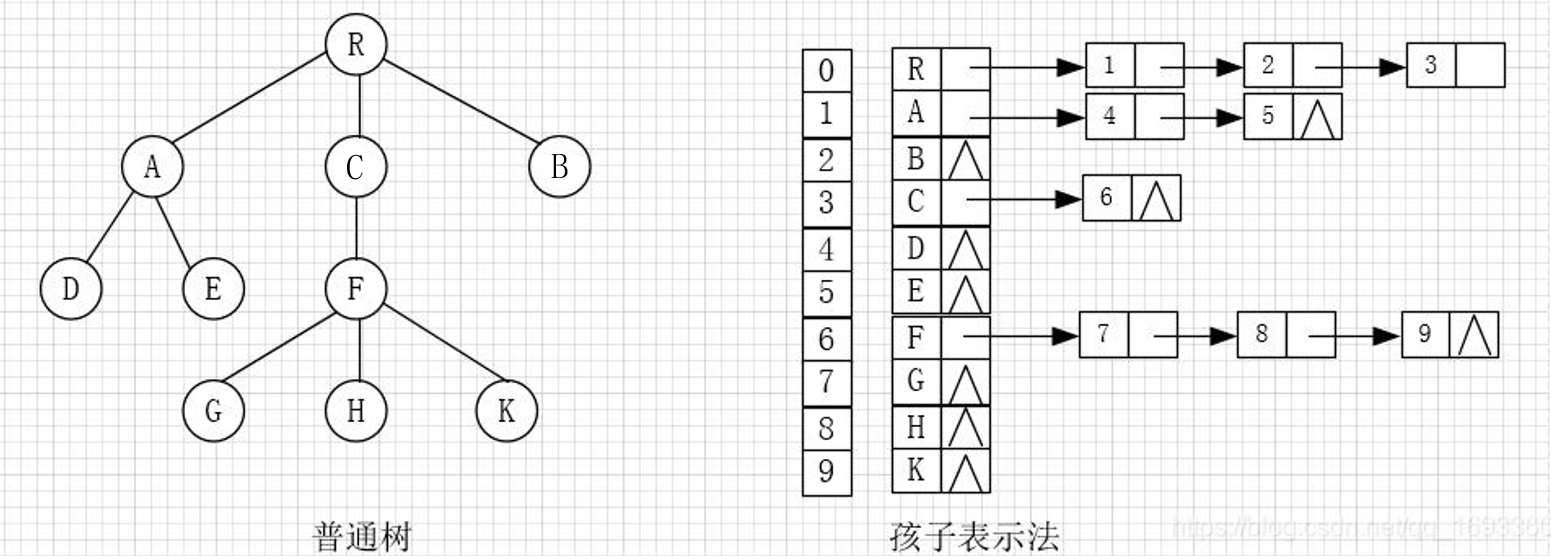
?特点:孩子表示法这种存储方式寻找子女的操作非常直接,而寻找双亲的操作需要遍历n个结点中孩子链表指针域所指向的n个孩子链表。
?树的孩子表示法采用的是**“顺序表+链表”**的组合结构,其存储过程为,从树的根结点开始,使用顺序表依次存储树中各个结点,并给每一个结点分配一个链表,用于存储各个结点的孩子结点位于顺序表中的位置。如果该结点没有孩子结点(即是叶子结点),则该结点的链表为空链表。
?对于上图的完整实现代码如下:
#include<bits/stdc++.h>
using namespace std;
#define MaxSize 100
typedef struct ChildNode{ //链表中每个结点的定义
//链表中每个结点存储的不是数据本身,而是数据在数组中存储的位置下标
int child;
struct ChildNode *next;
}ChildNode;
typedef struct{ //树中每个结点的定义
char data; //结点的数据类型
ChildNode *firstchild; //孩子链表头指针
}CHNode;
typedef struct{
CHNode nodes[MaxSize]; //存储结点的数组
int n;
}CTree;
//树中结点初始化
CTree InitTree(CTree tree){
cout<<"请输入结点总数:";
cin>>tree.n;
for(int i=0; i<tree.n; i++){
cout<<"请输入第"<<i+1<<"个结点的值:";
fflush(stdin);
cin>>tree.nodes[i].data;
//链表结点
tree.nodes[i].firstchild = (ChildNode *)malloc(sizeof(ChildNode));
tree.nodes[i].firstchild->next = NULL;
cout<<"请输入结点"<<tree.nodes[i].data<<"的孩子结点数量:";
int num;
cin>>num;
if(num != 0){
ChildNode *p = tree.nodes[i].firstchild; //p为操作指针
for(int j=0; j<num; j++){
ChildNode *q = (ChildNode *)malloc(sizeof(ChildNode)); //新建结点
q->next = NULL;
cout<<"请输入第"<<j+1<<"个孩子结点在顺序表中的存储位置: ";
cin>>q->child;
p->next = q;
p = p->next;
}
}
}
return tree;
}
void FindKids(CTree tree, char a){
int flag = 0;
for(int i=0; i<tree.n; i++){
if(tree.nodes[i].data == a){
cout<<a<<"的所有孩子结点为: ";
ChildNode *p = tree.nodes[i].firstchild->next;
while(p){
flag = 1;
//输出所有的孩子结点
cout<<tree.nodes[p->child].data<<" ";
p = p->next;
}
break;
}
}
if(flag == 0){
cout<<"此结点为叶子节点"<<endl;
}
}
int main(){
CTree tree;
tree = InitTree(tree);
char a;
cout<<"请输入要查找其孩子结点的结点:";
cin>>a;
FindKids(tree, a);
return 0;
}
?运行结果为:
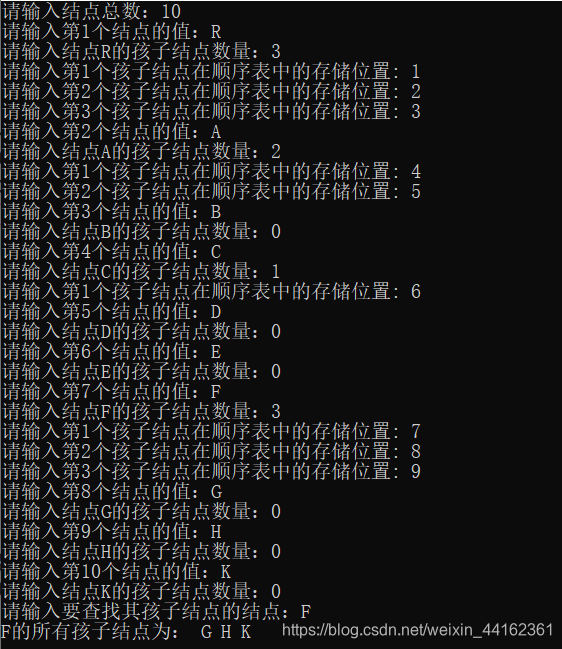
<3>孩子兄弟表示法
?孩子兄弟表示法又称二叉树表示法,即以二叉链表作为树的存储结构。
?孩子兄弟表示法使每个结点包括三部分内容:结点值、指向结点第一个孩子结点的指针、指向结点下一个兄弟结点的指针(沿此域可以找到结点的所有兄弟结点)。
?结点结构示意图:

?孩子兄弟表示法的具体实例:
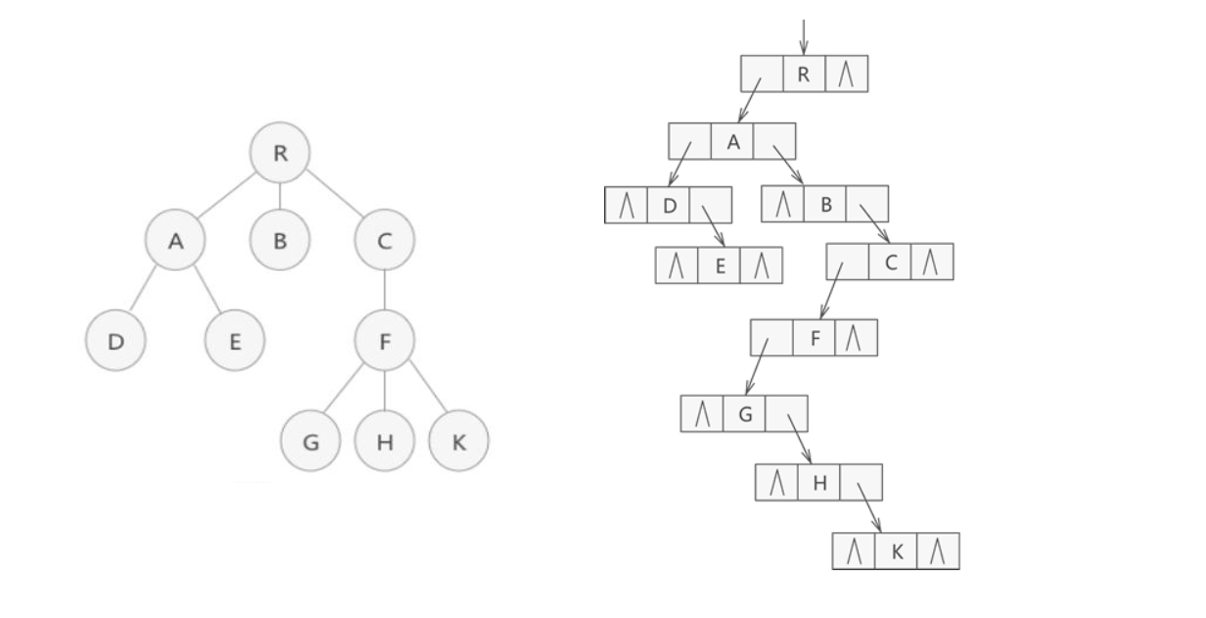
?孩子兄弟表示法的存储结构描述如下:
typedef struct CSNode{
char data; //数据域
struct CSNode *firstchild, *nextsibling; //第一个孩子和右兄弟指针
}CSNode, *CSTree;
?特点:孩子兄弟存储表示法比较灵活,其最大的优点是可以方便的实现树转换为二叉树的操作,易于查找结点的孩子等;缺点是从当前结点查找其双亲结点比较麻烦。
?若为每一个结点增设一个parent域指向其父结点,则查找结点的父结点也很方便。
?通过孩子兄弟表示法,任意一棵普通树都可以相应转化为一棵二叉树,也就是说,任意一棵普通树都有唯一一颗二叉树与之对应。
?这种方式的代码实现与二叉树的操作大致相同,故不再给出。