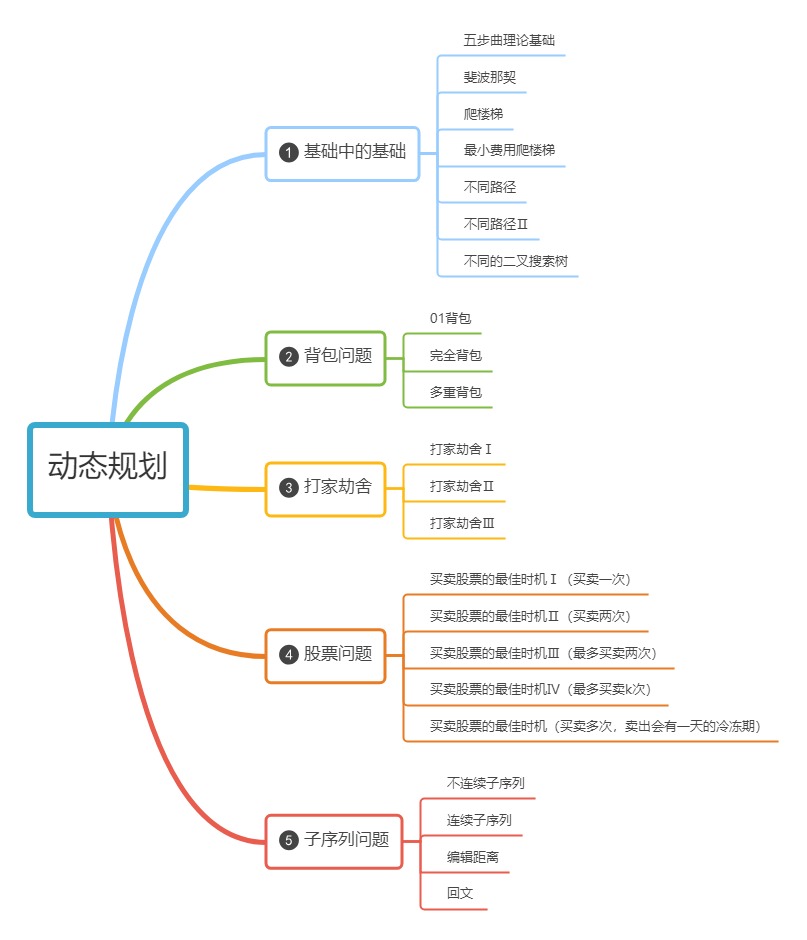
继续按照这个思维导图刷题~
打家劫舍
打家劫舍Ⅰ

class Solution {
public:
int rob(vector<int>& nums) {
vector<vector<int>> dp(2, vector<int>(nums.size()+1, 0));
dp[0][1] = 0, dp[1][1] = nums[0];
int res = 0;
for(int i = 1; i <= nums.size(); i++){
dp[0][i] = max(dp[1][i-1], dp[0][i-1]);
dp[1][i] = dp[0][i-1] + nums[i-1];
res = max(res, max(dp[0][i], dp[1][i]));
}
return res;
}
};
由于这里需要记录两种状态,所以开了二维数组:一种是抢当前这家,一种是不抢所能赚的最多的小钱钱。
啊哦,题解说没必要,一维就可以,让我们来看看题解怎么做的⑧
哈!它和我最初的思路一样!dp[i] 表示蹲在第 i 家房顶上(并不一定要偷这家)所能偷窃的最高金额。
也和我一样,考虑了第 ( i - 2 ) 家,看起来我的直觉还是蛮准的。明白了!下笔吧!
class Solution {
public:
int rob(vector<int>& nums) {
int houses = nums.size();
int dp[houses+1];
memset(dp, 0, sizeof dp);
dp[0] = 0, dp[1] = nums[0];
for(int i = 2; i <= houses; i++){
dp[i] = max(dp[i-1], dp[i-2] + nums[i-1]);
}
return dp[houses];
}
};
打家劫舍Ⅱ
变成了一个环,那么无非考虑两种情况:
- 第一户偷,最后一户必不能偷;
- 第一户不偷,最后一户随意。
class Solution {
public:
int rob(vector<int>& nums) {
int houses = nums.size();
int res = 0;
int dp[houses+1];
memset(dp, 0, sizeof dp);
//case 1 偷第一户,那么最后一户不能偷
dp[0] = 0, dp[1] = nums[0];
for(int i = 2; i <= houses; i++){
if(i == houses) dp[i] = dp[i-1];
else dp[i] = max(dp[i-1], dp[i-2] + nums[i-1]);
}
res = dp[houses];
//case2 第一户不偷,最后一户随意
dp[0] = 0, dp[1] = 0;
for(int i = 2; i <= houses; i++){
dp[i] = max(dp[i-1], dp[i-2] + nums[i-1]);
}
res = max(res, dp[houses]);
return res;
}
};
虽然比较死板,但是解决了问题,老规矩,看看题解有没有新方法呢!
他的方法也是做两遍,一遍只考虑首个元素和中间元素(去掉最后一个);一遍是只考虑中间元素和最后一个(去掉首个元素),与我们的思路大同小异,此处就不贴代码啦!
打家劫舍Ⅲ
本题涉及二叉树,兹事体大(这个还没复习)先溜了呜呜,等会了再回来追更。。。
股票问题
买卖股票的最佳时机Ⅰ(买卖一次)

class Solution {
public:
int maxProfit(vector<int>& prices) {
int s = prices.size();
int dp[s][2];
dp[0][0] = -prices[0], dp[0][1] = 0;
for(int i = 1; i < s; i++){
dp[i][0] = max(dp[i-1][0], -prices[i]);
dp[i][1] = max(dp[i-1][1], dp[i-1][0] + prices[i]);
}
return dp[s-1][1];
}
};
第一是因为动作只有一次;
第二是因为买卖当天看不到结果。
所以我们要定义可延续的状态作为DP数组(便于递推)
买卖股票的最佳时机(尽可能多次)
审题!审题!这些题目的区别可能就在几个字之间。
之前以为是最多两次(因为样例和思维导图的误导)捣鼓了半天,还是只过了1/3的样例,我用了四种状态,试着把买入第二支股票的状态初始化为负无穷(也就是0x8f)也不行。

class Solution {
public:
int maxProfit(vector<int>& prices) {
int s = prices.size();
int dp[s][2];
memset(dp, 0, sizeof dp);
dp[0][0] = -prices[0];
for(int i = 1; i < s; i++){
dp[i][0] = max(dp[i-1][0], dp[i-1][1] - prices[i]);
dp[i][1] = max(dp[i-1][1], dp[i-1][0] + prices[i]);
}
return dp[s-1][1];
}
};
买卖股票的最佳时机Ⅲ(最多两次)
说曹操曹操到,(。・?・)ノ゙嗨,刚刚说审错题了不会做,结果就真来了——最多买卖两次。
买入第二支股票的状态应该初始化为 -prices[0] 啊,没想到叭!用上一题的错误代码,加上这个初始化就过了~
原来是初始化没整对,嗨呀,应该多尝试几次的,早有预感,为什么不按预感行事呢!

class Solution {
public:
int maxProfit(vector<int>& prices) {
int s = prices.size();
int dp[s][4];
memset(dp, 0, sizeof dp);
dp[0][0] = -prices[0], dp[0][2] = -prices[0];
for(int i = 1; i < s; i++){
dp[i][0] = max(dp[i-1][0], -prices[i]);
dp[i][1] = max(dp[i-1][1], dp[i-1][0] + prices[i]);
dp[i][2] = max(dp[i-1][2], dp[i-1][1] - prices[i]);
dp[i][3] = max(dp[i-1][3], dp[i-1][2] + prices[i]);
}
return dp[s-1][3];
}
};
买卖股票的最佳时机(最多k次)
套路都是一样的,只需要将 2 改成 k 即可。
class Solution {
public:
int maxProfit(int k, vector<int>& prices) {
int s = prices.size();
if(s == 0 || k == 0) return 0;
vector<vector<int>> dp(s, vector<int>(2*k, 0));
for(int i = 0; i < 2*k; i+=2) dp[0][i] = -prices[0];
for(int i = 1; i < s; i++){
dp[i][0] = max(dp[i-1][0], -prices[i]);
dp[i][1] = max(dp[i-1][1], dp[i-1][0] + prices[i]);
for(int j = 2; j < 2*k; j+=2){
dp[i][j] = max(dp[i-1][j], dp[i-1][j-1] - prices[i]);
dp[i][j+1] = max(dp[i-1][j+1], dp[i-1][j] + prices[i]);
}
}
return dp[s-1][2*k-1];
}
};
最佳买卖股票时期(含冷冻期)
状态0 : 买入(前一天买入;前一天冷冻)
状态1 : 卖出(前一天卖出;今天卖)
状态2 : 冷冻(昨天卖)
class Solution {
public:
int maxProfit(vector<int>& prices) {
int s = prices.size();
int dp[s][3];
memset(dp, 0, sizeof dp);
dp[0][0] = -prices[0];
for(int i = 1; i < s; i++){
dp[i][0] = max(dp[i-1][0], dp[i-1][2] - prices[i]);
dp[i][1] = max(dp[i-1][1], dp[i-1][0] + prices[i]);
dp[i][2] = dp[i-1][1];
}
return max(dp[s-1][1], dp[s-1][2]);
}
};
买卖股票的最佳时期(含手续费)

class Solution {
public:
int maxProfit(vector<int>& prices, int fee) {
int s = prices.size();
int dp[s][2];
memset(dp, 0, sizeof dp);
dp[0][0] = -prices[0];
for(int i = 1; i < s; i++){
dp[i][0] = max(dp[i-1][0], dp[i-1][1] - prices[i]);
dp[i][1] = max(dp[i-1][1], dp[i-1][0] + prices[i] - fee);
}
return (dp[s-1][1]);
}
};
股票问题总结
从买卖一次到买卖尽可能多次,从买卖最多两次到最多 k 次(这个要注意初始化问题),从有冷冻期到有手续费,我们过五关斩六将,手法日渐纯熟,DP也不太难嘛,只要掌握了其精髓,任其变化都不怕!
还有一点想说明一下,就是到底是用
dp[i][0] = max(dp[i-1][0], -prices[i]);
还是用
dp[i][0] = max(dp[i-1][0], dp[i-1][1]-prices[i]);
取决于是否可以无限次,如果说可以无限次买卖,就是下面那种;如果规定了只能最多进行 k 次,那么就是上面那种。
无限次的情况中,循环里只有两行代码,买入时有可能已经卖出有了本金;但是有限次的话,第 0 天不可能卖出(没有本金),第 1 天如果还买入的话,就只有负值的份儿。关于最多 k 次的话,除去第一次,后面的次数再买入就可能已经有本金了,所以可以用下面那行代码。
或者解决这个问题还可以再增加一个状态,叫做 “什么也不做” ,状态0,初始化为0,后面的状态顺延,这样就可以在买卖 K 次时进行整合,也是一种方法。(如下)
dp[0][1] = -prices[0], dp[0][3] = -prices[0];
for(int i = 1; i < prices.size(); i++){
dp[i][0] = dp[i-1][0];
dp[i][1] = max(dp[i-1][1], dp[i-1][0] - prices[i]);
dp[i][2] = max(dp[i-1][2], dp[i-1][1] + prices[i]);
dp[i][3] = max(dp[i-1][3], dp[i-1][2] - prices[i]);
dp[i][4] = max(dp[i-1][4], dp[i-1][3] + prices[i]);
}
那么到这里,打家劫舍和股票问题就刷完啦!还留下了一个伏笔,就是打家劫舍Ⅲ(二叉树居民楼)等我学好了二叉树再回来!下篇时子序列问题,刷完才算完,我和DP之间的,嗯,故事。
