题意
定义一个可重集合 s ,一次操作为将 s 中最大值减去 p 。
小 L 想知道,如果给你 s 和 p 以及操作次数 k ,你能求出最后的集合吗?
k<=10^18 。
Solution:
因为思路比较有借鉴意义,所以写了。
首先 k 的范围不允许模拟。考虑到最大值有单调性,所以二分最终序列最大值,因为每次减去的数一定,可以直接算。可以证明剩下的操作不超过 n 次,暴力枚举即可。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int n;
ll k,p,Max,cnt;
ll a[1000005];
vector<ll> ans;
priority_queue<ll> q;
ll check(ll mid) {
cnt=0;
for(int i=1;i<=n;i++) {
if(a[i]>mid) {
ll tmp=(a[i]-mid+p-1)/p;
cnt+=tmp;
}
}
return cnt;
}
int main() {
scanf("%d%lld%lld",&n,&k,&p);
for(int i=1;i<=n;i++) {
scanf("%lld",&a[i]),Max=max(Max,a[i]);
}
sort(a+1,a+1+n);
if(p==0) {
for(int i=1;i<=n;i++) printf("%lld ",a[i]);
return 0;
}
ll l=-1e18,r=Max,res=0;
while(l<=r) {
ll mid=(l+r)>>1;
if(check(mid)<=k) {
r=mid-1,res=mid;
}
else {
l=mid+1;
}
}
// cout<<res<<endl;
check(res);
for(int i=1;i<=n;i++) {
if(a[i]>res) {
ll tmp=(a[i]-res+p-1)/p;
a[i]-=tmp*p;
}
q.push(a[i]);
}
for(int i=1;i<=k-cnt;i++) {
ll x=q.top(); q.pop();
q.push(x-p);
}
while(q.size()) {
ans.push_back(q.top()); q.pop();
}
for(int i=n-1;i>=0;i--) printf("%lld ",ans[i]);
}
第二种思路是二分临界点。考虑 Max-Min<=p 的情况,此时每次操作最大数时都会放在队列末尾,显然具有单调性。
于是我们想到二分 i 值,我们发现 i=n 时一定成立(因为 i 第一次被取出说明其他数都减的比它小且不超过 p),所以只需要判断第 i 个数第一次被取出时是否 Max-Min<=p 即可。常数较小。
进一步发现没必要二分,直接减到比 a[n] 小即可。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
//代码有锅,应该是细节问题
int n;
ll k,p,Max,cnt;
ll a[1000005];
vector<ll> ans;
priority_queue<ll> q;
ll check(int mid) {
cnt=0;
for(int i=1;i<mid;i++) {
if(a[i]>a[mid]) {
ll tmp=(a[i]-a[mid]+p-1)/p;
cnt+=tmp;
}
}
return cnt;
}
int main() {
scanf("%d%lld%lld",&n,&k,&p);
for(int i=1;i<=n;i++) {
scanf("%lld",&a[i]),Max=max(Max,a[i]);
}
sort(a+1,a+1+n),reverse(a+1,a+1+n);
if(p==0) {
for(int i=1;i<=n;i++) printf("%lld ",a[i]);
return 0;
}
if(n==1) {
printf("%lld",a[1]-k*p);
return 0;
}
ll l=1,r=n,res=0;
while(l<=r) {
ll mid=(l+r)>>1;
if(check(mid)<=k) {
l=mid+1,res=mid;
}
else {
r=mid-1;
}
}
// cout<<res<<endl;
check(res); k-=cnt;
if(res==n) {
ll tmp=k/n; k%=n; //n 轮一个循环, 取到了 a[n] .
for(int i=1;i<=n;i++) {
if(a[i]>a[res]) {
ll tmp2=(a[i]-a[res]+p-1)/p;
a[i]-=tmp2*p;
}
a[i]-=tmp*p;
q.push(a[i]);
}
for(int i=1;i<=k;i++) {
ll x=q.top(); q.pop();
q.push(x-p);
}
}
else {
//这里每次把最大数减到比次大数小,可以证明操作次数不超过 n
for(int i=1;i<=n;i++) {
if(a[i]>a[res]) {
ll tmp2=(a[i]-a[res]+p-1)/p;
a[i]-=tmp2*p;
}
q.push(a[i]);
}
while(k) {
ll x=q.top(); q.pop(); ll y=q.top();
ll tmp=(x-y)/p+1;
if(tmp<=k) {
x-=tmp*p;
k-=tmp;
q.push(x);
}
else {
x-=k*p;
q.push(x);
break;
}
}
}
while(q.size()) {
ans.push_back(q.top()); q.pop();
}
for(int i=n-1;i>=0;i--) printf("%lld ",ans[i]);
}
讲到单调性,来看这道题:
小L的疑惑
结论:不能支付的面额可以表示为 t-xa-yb(x>=0,y>=0) 其中 t=ab-a-b 。
由于 k<=10^7 ,通过分析单调性,可以得到线性做法:
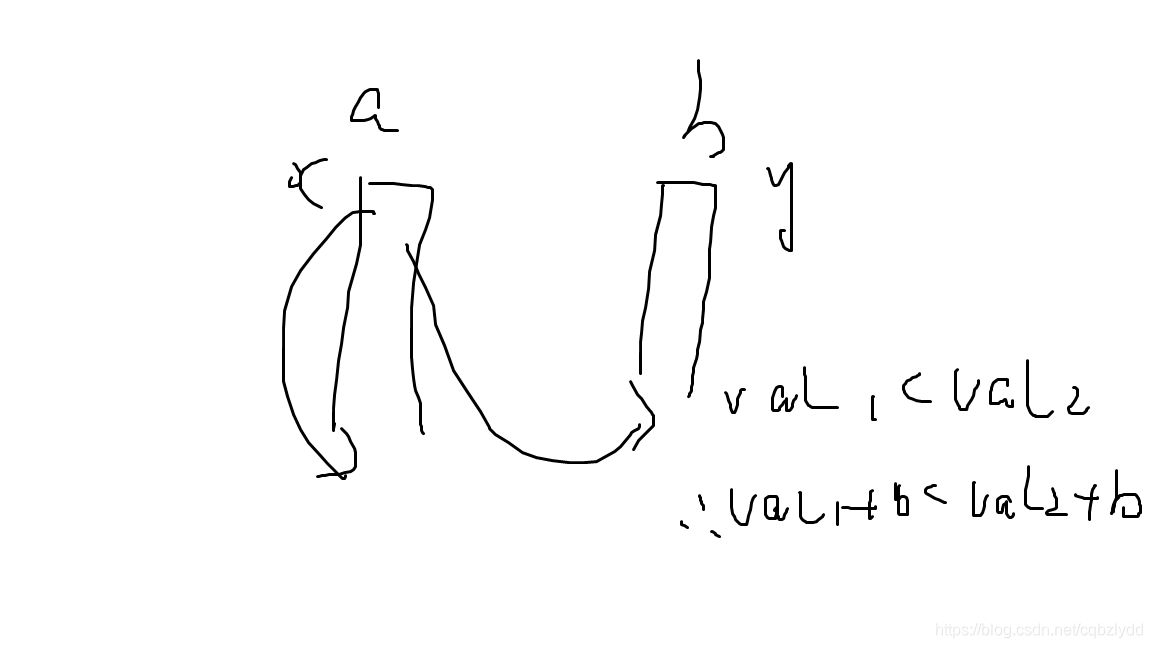
维护两个队列,初始将 t 放入 a 队列,每次取出两个队首最大值,如果是 b 栈就放入队尾,a 栈则放入两个栈的队尾,由于每次入栈的规则相同,而答案单调递增,所以两个队列具有单调性。
上述做法可以扩展到 n 栈的做法,时间复杂度 O(nk) 。
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn=1e7+10;
queue<ll> q[2];
ll res;
int main()
{
long long a,b;
int k;
scanf("%lld%lld%d",&a,&b,&k);
q[0].push(a*b-a-b);
for(int i=1;i<=k;i++) {
if(!q[1].size()||q[0].front()>q[1].front()) {
res=q[0].front(); q[0].pop();
q[0].push(res-a),q[1].push(res-b);
}
else {
res=q[1].front(); q[1].pop();
q[1].push(res-b);
}
}
printf("%lld",res);
return 0;
}