前言

本文主要记录二叉树的遍历方法，文章的主要知识点来源为：
https://leetcode-cn.com/problems/binary-tree-preorder-traversal/solution/leetcodesuan-fa-xiu-lian-dong-hua-yan-shi-xbian-2/
对于二叉树的遍历主要有三种形式，前序遍历、中序遍历、后序遍历；
所谓前序遍历，是指从根节点开始，对每一个节点，都采用先遍历该节点，再遍历其左子节点，最后遍历其右子节点的方式；
所谓中序遍历，是指从根节点开始，对每一个节点，都采用先遍历其左子节点，再遍历该节点，最后遍历其右子节点的方式；
所谓后序遍历，是指从根节点开始，对每一个节点，都采用先遍历其左子节点，再遍历其右子节点，最后遍历该节点的该当；

以一个二叉树图来说明一下。
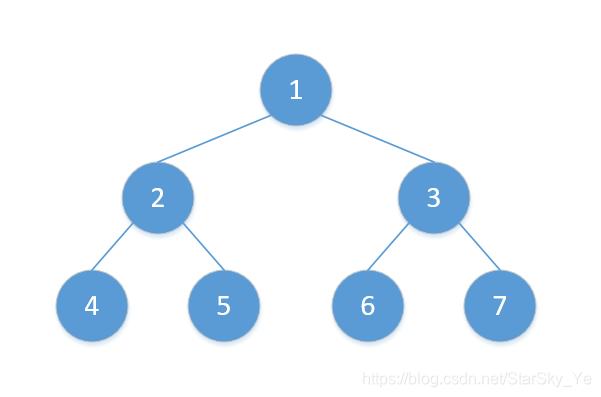
在这里插入图片描述
对于上前所示的二叉树，其三种遍历方式的结果为：
前序遍历：1 2 4 5 3 6 7
中序遍历：4 2 5 1 6 3 7
后充遍历：4 5 2 6 7 3 1

下述中所用到的TreeNode数据结构如下所示：

class TreeNode:
    def __init__(self, value, left=None, right=None) -> None:
        self.m_value = value
        self.m_left = left
        self.m_right = right

    def setLeftChild(self, left):
        self.m_left = left

    def setRightChild(self, right):
        self.m_right = right

一、用递归法实现遍历

1.1 前序遍历

result = list()

def preOrderRecur(root: TreeNode):
	# 若为空则返回
    if not root:
        return
        
    # 先记录当前节点的值
    result.append(root.m_value)
    # 再递归记录其左子树的各个值
    preOrderRecur(root.m_left)
    # 最后递归记录其右子树的各个值
    preOrderRecur(root.m_right)

1.2 中序遍历

result = list()
def inOrderRecur(root: TreeNode):
    if not root:
        return
    # 先递归遍历其左子树的各个值
    inOrderRecur(root.m_left)
    # 再记录当前值
    result.append(root.m_value)
    # 最后递归遍历其右子树的各个值
    inOrderRecur(root.m_right)

1.3 后序遍历

result = list()
def postOrderRecur(root: TreeNode):
    if not root:
        return
    # 先递归遍历其左子树的各个值
    postOrderRecur(root.m_left)
    # 再递归遍历其右子树的各个值
    postOrderRecur(root.m_right)
    # 最后记录当前节点值
    result.append(root.m_value)

二、用迭代法实现遍历

本质上是在模拟递归，因为在递归的过程中使用了系统栈，所以在迭代的解法中常用数据结构stack来模拟系统栈，在具体的python实现中，本文用list列表，且仅对最后一个元素作添加和删除操作来模拟栈，同时要注意的是栈是先进后出的数据结构。

2.1 前序遍历

基本的步骤是：
1 每访问到一个节点时，记录该节点的值；
2 之后按前序遍历的定义是要先记录左子树的值，再记录右子树的值，而栈是先进后出的结构特点，所以应该让其右子节点先入栈，再入左子节点。

result = list()
def preOrderIteration(root: TreeNode):
    if not root:
        return
    
    nodeStack = list()
    # 当前节点先入栈
    nodeStack.append(root)
    while len(nodeStack):
    	# 从栈中取出一个节点，表示的是当前遍历到该节点了
        node = nodeStack.pop()
        result.append(node.m_value)
  
        if node.m_right:
            nodeStack.append(node.m_right)
            
        if node.m_left:
            nodeStack.append(node.m_left)

2.2 中序遍历

基本步骤是：
1 创建一个Stack，以便于按左中右的顺序输出节点。
2 尽可能的将这个节点的左子树压入Stack，此时栈顶的元素是最左侧的元素，其目的是找到一个最小单位的子树(也就是最左侧的一个节点)，并且在寻找的过程中不断记录来源，这样才能逐步返回上层。在返回上层的时候，就意味着已经处理完毕左子树了。
3 当处理完最小单位的子树时，返回到上层处理了中间节点，记录下当前值。
4 判断如果有右节点，其也要对其进行一次中序遍历

result = list()
def inOrderIteration(root: TreeNode):
    if not root:
        return

    currentNode = root
    nodeStack = list()
    while len(nodeStack) or currentNode:
        while currentNode:
            nodeStack.append(currentNode)
            currentNode = currentNode.m_left

        node = nodeStack.pop()
        result.append(node.m_value)
        if node.m_right:
            currentNode = node.m_right

2.3 后序遍历

2.3.1 后序解法一

1 前序遍历的过程是中左右，而后序遍历的过程是左右中。
2 修改前序遍历的实现过程为，中右左；即在压栈时，优先压入左子树，再压入右子树；
3 将步骤2得到的结果，倒序输出，就是后序遍历所期望的左右中的结果。

result = list()
def postOrderIteration(root: TreeNode):
    if not root:
        return
    
    tmpResult = list()
    nodeStack = list()
    nodeStack.append(root)
    while len(nodeStack):
        node = nodeStack.pop()
        tmpResult.append(node.m_value)
        if node.m_left:
            nodeStack.append(node.m_left)
        
        if node.m_right:
            nodeStack.append(node.m_right)
        
    tmpResult.reverse()  
    result.extend(tmpResult)

2.3.2 后序解法二

基本步骤为：
1 用一个preNode，标记当前退出的节点是什么。
2 后序遍历的过程中，在遍历完左子树或右子树时，preNode都会回到其根结点。此时不应该再对该根结点的子节点做入栈操作，应该退回更上一层。

result = list()
def postOrderIteration2(root: TreeNode):
    if not root:
        return

    preNode = root
    nodeStack = list()

    nodeStack.append(root)
    while len(nodeStack):
    	# 注意，这里只是取栈顶元素，并没有出栈操作
        node = nodeStack[-1]
        if node.m_left and node.m_left != preNode and node.m_right != preNode:
        	# 左子节点存在，且当前节点不是从其左子树或者右子树回退回来的根节点，
        	# 此时可以入栈左子节点，以便于继续往左子树深入判断添加节点。
            nodeStack.append(node.m_left)
        elif node.m_right and node.m_right != preNode:
        	# 右子节点存在，且当前节点不是从其右子树回退回来的，意味着，
        	# 此时是遍历完了左子树后回退到根节点的，若此时有右子树的根节点，
        	# 需要继续入栈该节点，以遍历右子树。
            nodeStack.append(node.m_right)
        else:
        	# 走到这里，要么是已经访问到叶子节点了（即node.m_left和node.m_right都是None的结点，
        	# 或者是遍历完左右子树后，回退到其根结点了，此时需要记录该节点的值，
        	# 并更新preNode，记录当前处理的节点）
            preNode = nodeStack.pop()
            result.append(preNode.m_value)

三、测试验证

对代码作个测试验证。

def initTree():
    root = TreeNode(1)
    root_l = TreeNode(2)
    root_r = TreeNode(3)
    root_l_1 = TreeNode(4)
    root_l_2 = TreeNode(5)
    root_r_1 = TreeNode(6)
    root_r_2 = TreeNode(7)
    root_l.setLeftChild(root_l_1)
    root_l.setRightChild(root_l_2)
    root_r.setLeftChild(root_r_1)
    root_r.setRightChild(root_r_2)
    root.setLeftChild(root_l)
    root.setRightChild(root_r)

result = list()
if __name__ == "__main__":
    tree = initTree()
    preOrderRecur(tree)
    print("preOrderRecur", result)
    result.clear()

    inOrderRecur(tree)
    print("inOrderRecur", result)
    result.clear()

    postOrderRecur(tree)
    print("postOrderRecur", result)
    result.clear()

    preOrderIteration(tree)
    print("preOrderIteration", result)
    result.clear()

    inOrderIteration(tree)
    print("inOrderIteration", result)
    result.clear()

    postOrderIteration(tree)
    print("postOrderIteration", result)
    result.clear()

    postOrderIteration2(tree)
    print("postOrderIteration2", result)

最终的输出结果为：
preOrderRecur [1, 2, 4, 5, 3, 6, 7]
inOrderRecur [4, 2, 5, 1, 6, 3, 7]
postOrderRecur [4, 5, 2, 6, 7, 3, 1]
preOrderIteration [1, 2, 4, 5, 3, 6, 7]
inOrderIteration [4, 2, 5, 1, 6, 3, 7]
postOrderIteration [4, 5, 2, 6, 7, 3, 1]
postOrderIteration2 [4, 5, 2, 6, 7, 3, 1]