[数据结构与算法]leetcode124. 二叉树中的最大路径和(Python)

1、题目

路径 被定义为一条从树中任意节点出发，沿父节点-子节点连接，达到任意节点的序列。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点，且不一定经过根节点。
路径和 是路径中各节点值的总和。
给你一个二叉树的根节点 root ，返回其 最大路径和 。

题目可以简化为：对于给定的以root为根节点的二叉树，计算任意两个节点之间的路径和。并最终返回最大的那个路径和。

2、递归思路

对于给定的以root为根节点的二叉树，我们计算两个最大路径和。

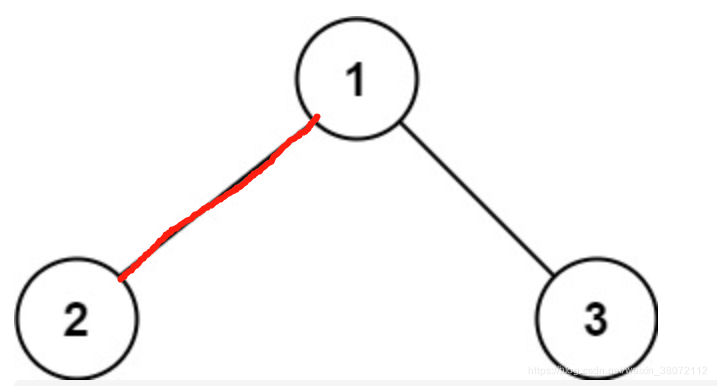
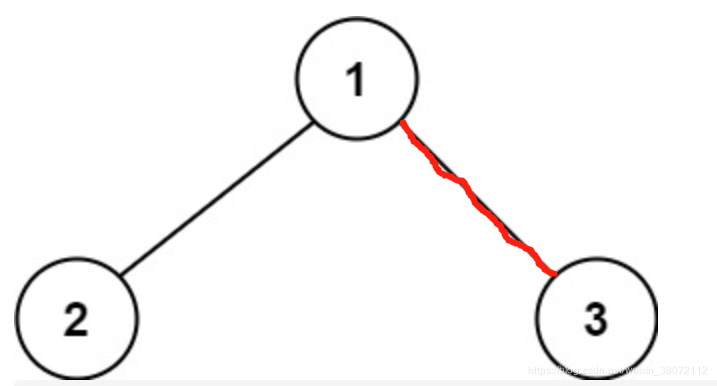
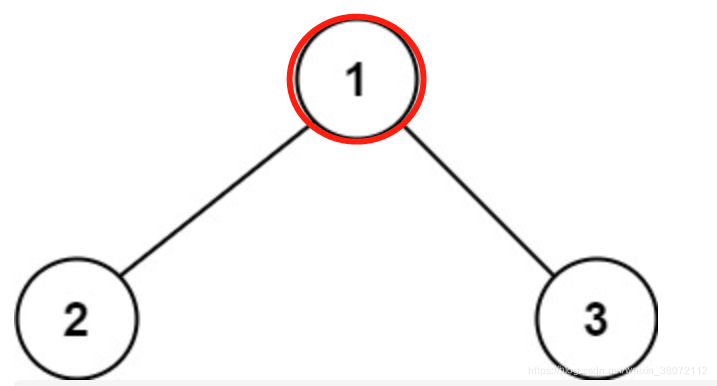
2.1、第一个是求以根节点为起点或终点的最大路径。在这里我们记为根有关路径（方便下面理解）。那么以根节点为起点或终点的所有路径有三种情况表示如下：

[root.left+root]：左节点的最大根有关路径和+ 根节点
[root.right+root]：右节点的最大根有关路径和 + 根节点
[root] ： 根节点
那么
最大根有关路径和为 max(root.left+root, root.right+root, root)

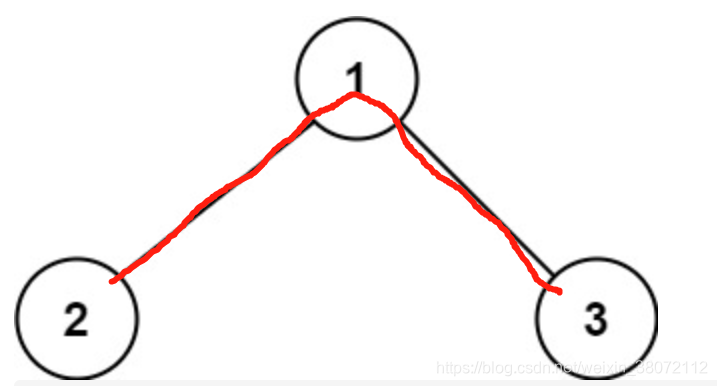
2.2、第二个则是和根节点无关的最大路径。换句话说，根节点不作为路径的起点或者终点。

同样有三种可能方式：
[root.left+root+root.right]：左节点的最大路径和 + 根节点+右节点的最大路径和
[root.left] ： 右节点的最大路径和
[root.right]：右节点的最大路径和
注意，上面说的最大路径和是：max（最大根有关路径，最大根无关路径）
那么：最大根无关路径和为 max(root.left+root+root.right, root.left, root.right)

2.3 最大路径和

那么对于根节点的最大路径和就是
max(2.1节, 2.2节)

3、实现代码如下：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def maxPathSum(self, root: TreeNode) -> int:
        
        def dfs(root):
            if not root:
                return float("-inf"), float("-inf")
            leftToRoot_max, leftNotToRoot_max = dfs(root.left)
            rightToRoot_max, rightNotToRoot_max = dfs(root.right)
            
            #最大根有关路径和
            toRoot_max = max(root.val, leftToRoot_max+root.val, rightToRoot_max+root.val)
            #最大根无关路径和
            notToRoot_max = max(leftToRoot_max+root.val+rightToRoot_max, leftNotToRoot_max, rightNotToRoot_max)
            # print(toRoot_max, notToRoot_max) 

            # 返回（最大根有关路径和， 最大路径和）
            return toRoot_max, max(notToRoot_max,toRoot_max)

        t, nt = dfs(root)
        return max(t,nt)