前言

求一个字符串中的最长回文子串问题，有很多方法。我弄懂了三种，在这里和大家分享

一、中心扩散法

中心扩散法是一个解决回文子串非常好用的方法。该方法的思想是将字符串从某个位置向左右扩散，只要左右对称位置的字符相同就可以一直扩散，知道不同停止，从左至右，扩散的下标之差就是该位置能得到的最大回文子串。
举个例子：
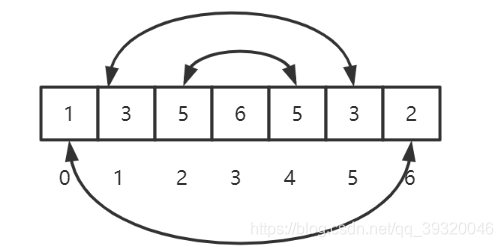
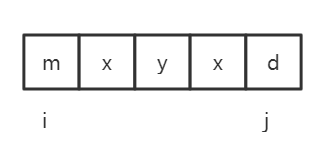
在这里插入图片描述
如图所示，称这个字符串为arr，从下标为3的6字符向左右扩散，arr[2]==arr[4],arr[1]==arr[5],arr[0]！=arr[6] 扩散停止，回文子串的起始位置为0，终止位置为5。
但是这个方法当回文子串的长度为偶数时会产生错误。
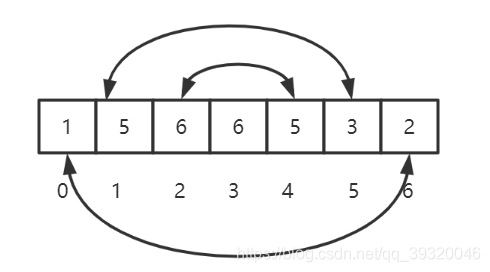
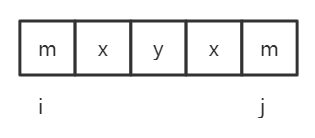
在这里插入图片描述
如上图所示，从下标为3的6字符向左右扩散，arr[2]！=arr[4],扩散停止，我们可以明显看到回文字符串的长度为4而非1。
所以我们在代码中进行扩散时，分别考虑了回文串为偶数和奇数的处理方法。
以图上的字符串为例子，我们让其向左向右的下标为i=3，j=3
和i=3-1,j=3分别进行计算，将较长的结果记录。
代码如下：

//range用来存储回文子串的首尾的下标
	static int[] range=new int[2];
	//主函数，遍历每个位置
	public static String maxLenPalindromesubstring(String str)
	{
		char[] chArr=str.toCharArray();
		for(int i=1;i<str.length();i++)
		{
			//回文串为奇数时
			process(chArr, i, i);
			//回文串为偶数时
			process(chArr, i-1, i);
		}
		return str.substring(range[0],range[1]);
	}
	//从一个中心像左右扩散过程函数
	public static void process(char[] chArr,int i,int j)
	{
		
		while(i>=0&&j<chArr.length)
		{
			if(chArr[i]==chArr[j])
			{
				i--;
				j++;
			}
			else
			{
				break;
			}
		}
		if(j-i-1>range[1]-range[0])
		{
			range[0]=i+1;
			range[1]=j;//j不减一是由于求子串函数substring是左闭右开的。
		}
	}

二、动态规划法

动态规划方法求字符串的回文子串也是可行的。我们想象一个行列均为长度字符串长度的dp表，dp[i][j]代表从i到j的字符串的最长回文子串的长度。如果arr[i]==arr[j]说明左右是相等的只要i-1到j-1也是回文串，那么从i到j就均为回文串。
那么如何如何确定i-1到j-1是否回文串呢？
只要i-1到j-1的长度和其最长回文子串长度相等，则可以证明i-1到j-1也是回文串。
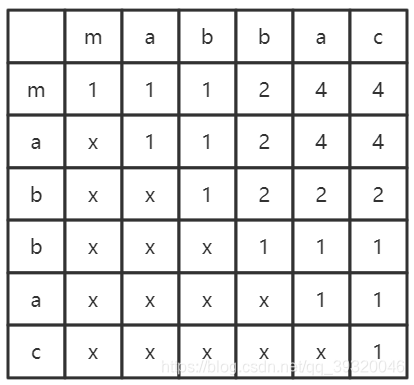
在这里插入图片描述

如上图假设要求字符串"mabbac"的最长回文子串则有上图所示的dp表。
由于表格的内容代表从i到j的最长回文子序列，所有当i>j的时候是没有意义的（比如从4到1的最长回文子序列）我们不考虑
这个回文子串可能性有一下几种：
a) 与i无关，与j有关 dp[i][j]=dp[i+1][j]
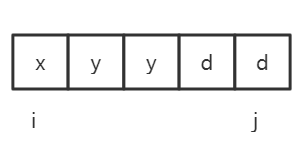
在这里插入图片描述
b)与i有关与j无关，此时dp[i][j]=dp[i][j-1]

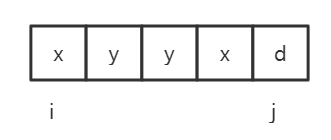
c) 与i、j都无关dp[i][j]=dp[i+1][j-1]
在这里插入图片描述
d) 与i、j都有关 dp[i]][j]=dp[i+1][j-1]+2(前提是arr[i]与arr[j]相等、且从i+1到j-1为回文串)

则根据以上规则可以填dp表的结果如下：

代码如下：

	public static int PalindromesubstringUseDp(String str)
	{
		char[] chArr=str.toCharArray();
		int[][] dp=new int[chArr.length][chArr.length];
		for(int i=0;i<dp.length;i++)
		{
			dp[i][i]=1;
			//对角线的回文子串均为1
		}
		for(int i=dp.length-2;i>=0;i--)
		{
			for(int j=i+1;j<dp[0].length;j++)
			{
				dp[i][j]=Math.max(dp[i+1][j],Math.max(dp[i][j-1], dp[i+1][j-1]));
				if(chArr[i]==chArr[j])
				{
					if(dp[i+1][j-1]==j-i-1)
					{
						dp[i][j]=Math.max(dp[i+1][j-1]+2, dp[i][j]);
					}
				}
			}
		}
		PrintArr2(dp);
		return dp[0][dp[0].length-1];
	}

三、Manacher求回文子串

manacher是非常有名的求最长回文子串的方法。这个方法还可以求出一个回文半径数组，可以在很多题目中有所应用。
该方法与中心扩散法很相似。两者都是根据扩散的距离找到最长的回文子串，但是该方法的优点并不是每次都是从到达位置的左右直接暴力扩，而是省略了许多不必要扩的位置。
再这个方法中我们为字符串之间加上’#‘来规避回文子串数为偶数时候难以扩散的问题。
比如字符串“12321”经过更改变成"#1#2#3#2#1#"
先来解释一下回文半径
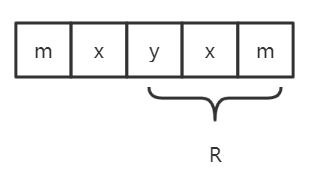
在这里插入图片描述
如上图所示从y到m的长度就是该回文串的回文半径，即为3。
我们将我们当前的位置称为i,
i之前所有位置的回文半径最远能够到达的位置成为R，
该回文半径是由C位置扩散而得的（C相当于R的圆心），
L为R的对称位置
i’为i的对称位置
我们开始对manacher算法进行分类：
1）R<=i 这个时候只能暴力扩。
2）R>i
a) i’的回文半径在L到R范围内
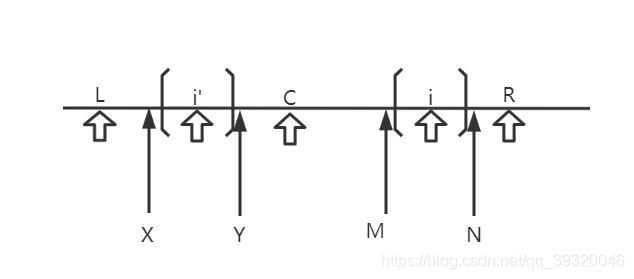
在这里插入图片描述
如图所示则R(i)==R(i’)，不需要再扩。
证明假设i的半径可以更大。假设arr[M]==arr[N]由于LR范围内是回文，则arr[X]==arr[N]、arr[Y]==arr[M]那么arr[Y]==arr[X]这样的话R(i’)就与当前已只的半径不同，矛盾了。
b) i’的回文半径大于L到R范围了
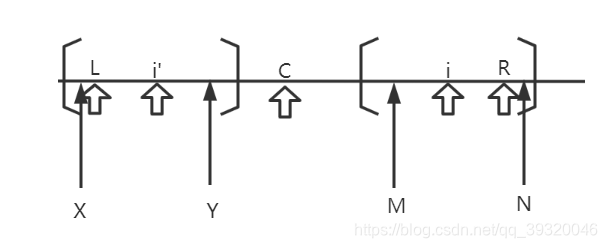
在这里插入图片描述
如图所示假设arr[M]==arr[N]，由于LR内是回文，所以，则arr[X]==arr[N]、arr[Y]==arr[M]那么arr[X]==arr[N]这样的话就说明有比R更大的回文子串，与R是当前最大的回文子串矛盾，所以arr[M]！=arr[N]。R(i)=R-i
3) i’的回文半径等于R-i了
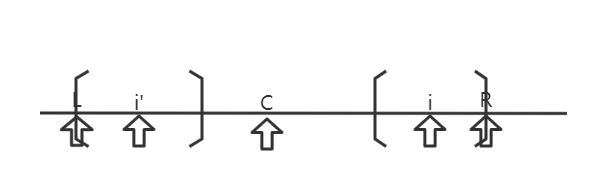
在这里插入图片描述
此时R(i)=R(i’)，对于i的半径大于R-i的位置是否相等需要暴力判断。
代码如下：

public static char[] reBuildStr(String str)
	{
		int index=0;
		char[] chArr=new char[str.length()*2+1];
		for(int i=0;i<chArr.length;i++)
		{
			chArr[i]=(i&1)==0?'#':str.charAt(index++);
		}
		return chArr;
	}
	public static int manacher(String str)
	{
		char[] res=reBuildStr(str);
		int R=-1;
		int C=-1;
		int[] pArr=new int[res.length];
		int max=0;
		for(int i=0;i<res.length;i++)
		{
			//这里跳过不需要检查的部分
			pArr[i]=R>i?Math.min(R-i, pArr[2*C-i]):1;
			while(i-pArr[i]>=0&&i+pArr[i]<res.length)
			{
				if(res[i-pArr[i]]==res[i+pArr[i]])
				{
					pArr[i]++;
				}
				else
				{
					break;
				}
			}
			if(i+pArr[i]>R)
			{
				R=i+pArr[i];
				C=i;
			}
			if(pArr[i]>max)
				max=pArr[i];
		}
		return max-1;
	}