文章目录
第二章 线性表
2.1大纲要求
(一)线性表的基本概念
(二)线性表的实现
?1.顺序存储
?2.链式存储
(三)线性表的应用
2.2 线性表的基本概念
线性表的定义:线性表是具有相同特性元素的一个有限序列
线性表的存储结构:顺序存储和链式存储,也就是顺序表和链表,
?????????顺序表的定义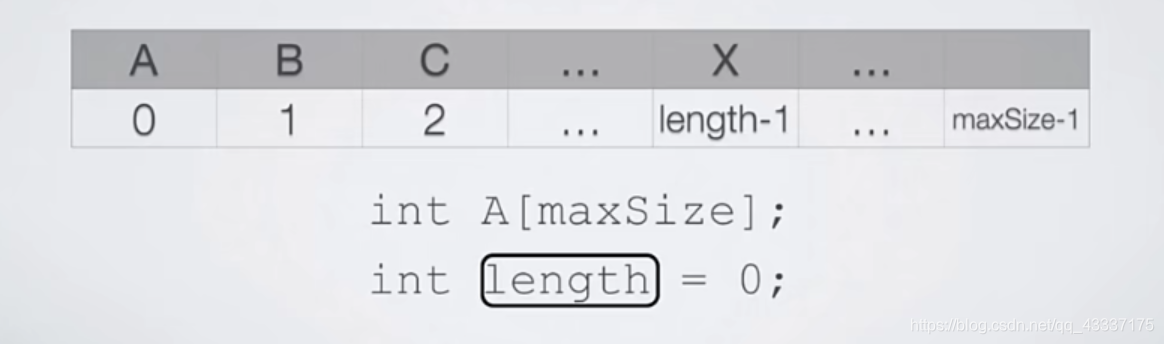
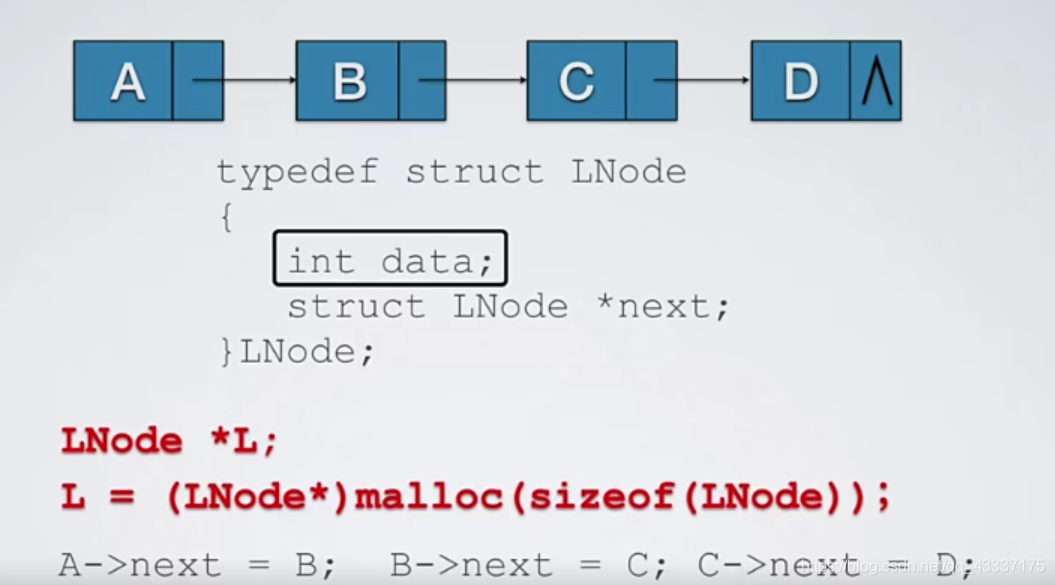
?????????链表的定义
| 存储结构 | 逻辑上 | 物理地址 |
|---|---|---|
| 顺序表 | 相邻 | 相邻 |
| 链表 | 相邻 | 不一定相邻 |
Head指针的作用是完整的标识了整个链表

单链表的判空条件是:
有头结点的单链表:Head->next = NULL
无头结点的单链表:Head = NULL
双链表

与单链表的区别就是给每个结点增加了指向前驱的指针。
判空条件与单链表相同。
循环单链表

循环单链表的判空条件是:
有头结点的循环单链表:Head->next = Head
不带头结点的循环单链表:Head = NULL
循环双链表:
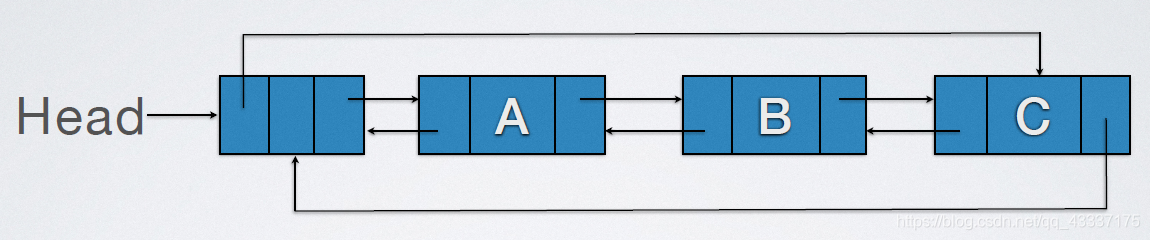
循环双链表的判空条件是:
有头结点:Head->next=Head或Head->prior=NULL
不带头结点的循环单链表:Head = NULL
习题一:

#include<iostream>
#include<cmath>
using namespace std;
#define MIN 0.001
#define MAXSIZE 100
int compare(float A[],int alen,float B[],int blen)
{
int i = 0;
while(i < alen && i < blen)
{
if (fabs(A[i]-B[i])<MIN)
++i;
else
break;
}
if(i >= alen && i >= blen)
return 0;
else if((i>=alen&&i<blen) || A[i]<B[i])
return -1;
else
return 1;
}
int main()
{
float A[MAXSIZE] = {1,2,3,4};
float B[MAXSIZE] = {1,2,3,4,5,6};
cout <<compare(A,4,B,6);
return 0;
}
2.3 存储结构特性对比
2.3.1 插入删除元素
2.3.1.1 顺序表插入
选定位置后,从后往前所有元素依次向右移动一个位置。从前往后会造成元素的覆盖。
2.3.1.2 顺序表删除
选定位置后,从前往后所有元素依次向左移动一个位置。从后往前会造成元素的覆盖。
2.3.1.3 结论
顺序表插入删除可能会导致大量的元素的连带操作,而链表不会。
2.3.2 取元素
在单链表中找到任意一个结点的位置不像顺序表那么简单,因为顺序表支持随机存储,而链表不支持。
2.3.3 存储空间
线性表采用顺序存储结构,必须占用一整片连续的存储空间,而采用链式存储结构则不需要这样;
从表的整体来看,一般顺序表存储空间利用率低于链表,但从单个的存储单元来看,顺序表的利用率高于链表。
存储密度是指结点本身所占的存储量和整个存储结构所占的存储量之比。
习题二:

选A,因为顺序表支持随机存储

选B,排除法

2.4 元素移动次数计算和静态链表
2.4.1 元素移动次数计算
主要应用于顺序表的插入和删除元素操作。
一个长度为n的顺序表可供插入的位置为n+1,所以在任意位置插入元素的概率为:
1
n
+
1
\frac{1}{n+1}
n+11?;
在i位置前插入元素,需要移动n-1个元素;
所以插入元素的平均移动次数为
n
2
\frac{n}{2}
2n?;
一个长度为n的顺序表可供插入的位置为n+1,所以在任意位置删除元素的概率为:
1
n
\frac{1}{n}
n1?;
在i位置前插入元素,需要移动n-i-1个元素;
所以插入元素的平均移动次数为
n
?
1
2
\frac{n-1}{2}
2n?1?;
2.4.2 静态链表
静态链表结点类型定义:
typedef struct
{
int data;
int next;
}SLNode;

构造一个长度为MAXSIZE的静态链表:
SLNode SLink[MAXSIZE];

int p = Ad0; //定义一个指针
SLink[p].data;//取p指向的结点值,相当于p->data
SLink[p].next;//取p的后继节点指针,相当于p->next
在p后插入结点q:
SLink[q].next = SLink[p].next;
Slink[p].next = q;
//类比 q.next = p.next p.next = q
习题三:

选B
A.两个都是O(1)
C.结点数目相同的链表占用存储空间相同

选C
A.并没有简单
B.不支持随机存储
D.不能很好的利用零散存储空间
2.5 线性表插入删除
2.5.1 单链表插入删除元素
2.5.1.1 插入
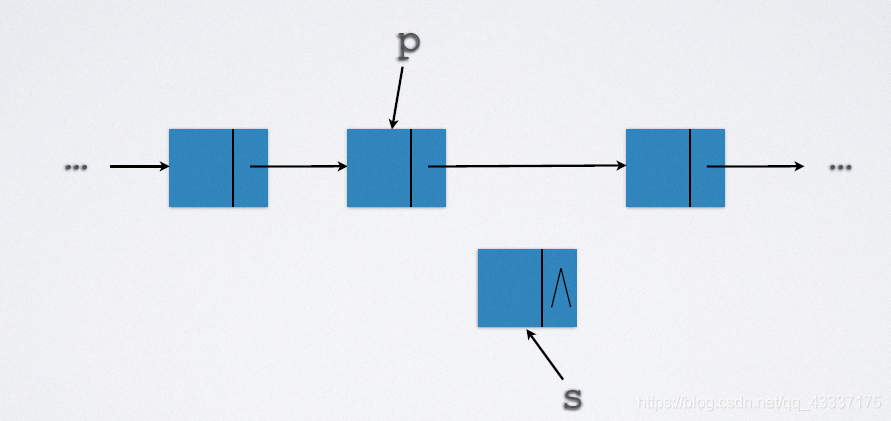
实现代码:
s->next = p->next;
p->next = s;
2.5.1.2 删除
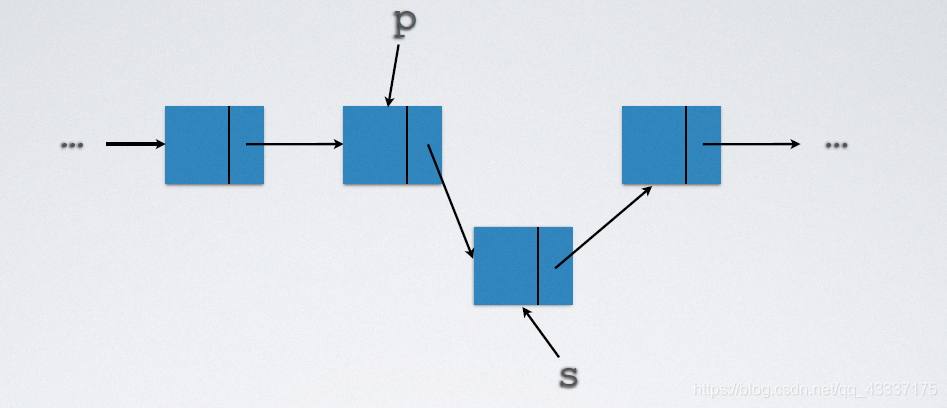
实现代码:
p->next = s->next;
free(s);

2.5.2 双链表插入删除元素
2.5.2.1 插入
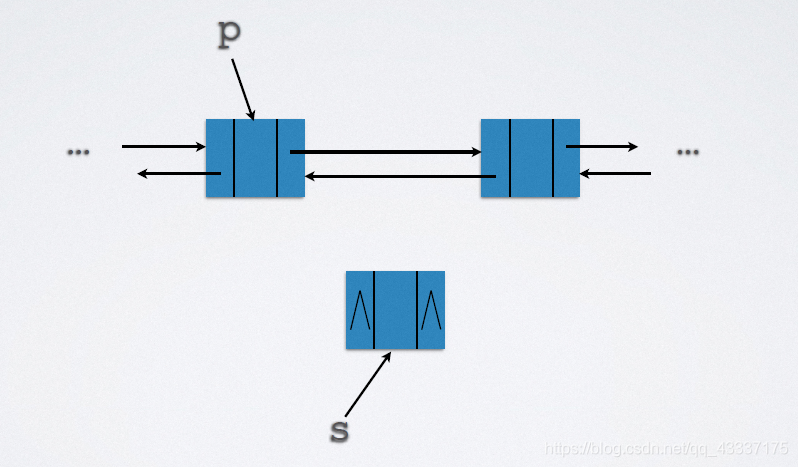
实现代码:
p->next = s-next;
s->prior = p;
p->next = s;
s->next->prior = s;
2.5.2.2 删除
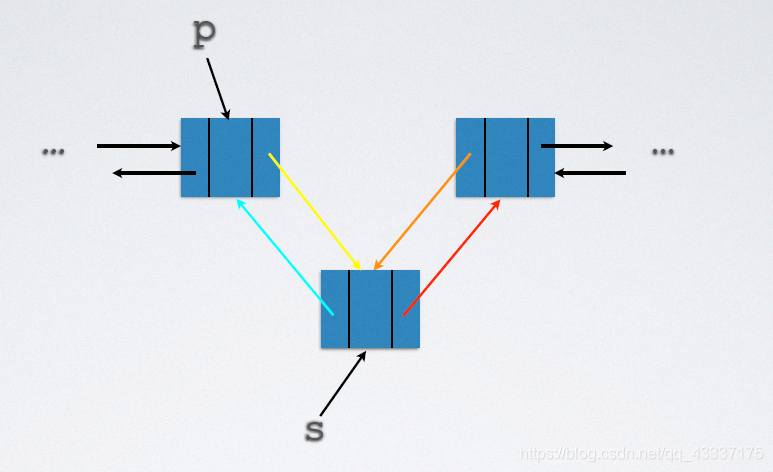
实现代码:
s->prior->next = s->next
s->next->prior = s->prior
free(s);
2.5.3 顺序表元素插入删除
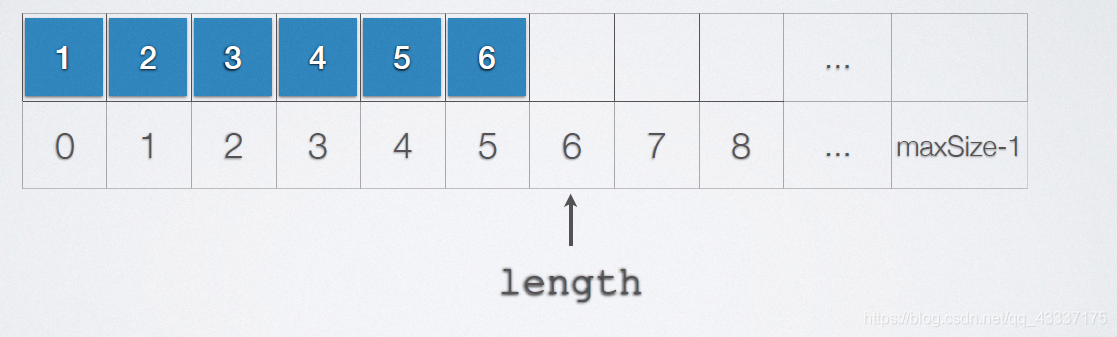
2.5.3.1 插入元素
可插入元素的位置:0-length;
当length=maxsize时不可以再插入元素;
移动元素从前往后进行。
插入操作实现代码:
int sqList[maxsize] = {1,2,3,4,...n};
int length = n;
int InsertElem(int sqList[],int &length,int p,int e)
{
if(p<0||p>length||length==maxsize)
return 0;
for(int i = length-1;i>=p;--i)
{
sqList[i+1]=sqList[i];
}
sqList[p]=e;
++length;
return 1;
}
2.5.3.2 删除元素
可插入元素的位置:0-length-1;
当length=0时不可以再插入元素;
移动元素从后往前进行。
删除操作实现代码:
int sqList[maxsize] = {1,2,3,4,...n};
int length = n;
int DeleteElem(int sqList[],int &length,int p,int e)
{
if(p<0||p>length-1)
return 0;
e = sqList[p];
for(int i = p;i<length-1;++i)
{
sqList[i]=sqList[i+1];
}
--length;
return 1;
}
习题四:

选B,链表长度越长,需要扫描的数据就越多

void DeleteElem(int sqList[],int &length,int p,int e)
{
int len = j-i+1;
for(int k = j+1;k<length;++i)
{
sqList[k-len]=sqList[k];
}
length-=len;
}

void del(LNode *L)
{
LNode *p = L-next,*q;
while(p->next !=NULL)
{
if(p->data==p->next-data)
{
q = p->next;
p->next = q->next;
free(q);
}
else
{
p = p->next;
}
}
}

void spilit(LNode *A,LNode *B)
{
B = (LNode*)molloc(sizeof(LNode));
LNode *p,*q,*r;
B->next = NULL;
r = B;
p = A;
while(p->next!=NULL)
{
if(p->next->data%2==0)
{
q = p->next;
p->next= q->next;
q->next =NULL;
r->next =q;
r = q;
}
else
{
p = p->next;
}
}
}
2.6 建表
2.6.1 顺序表建表
实现代码:

2.6.2 链表建表
实现代码(尾插法):
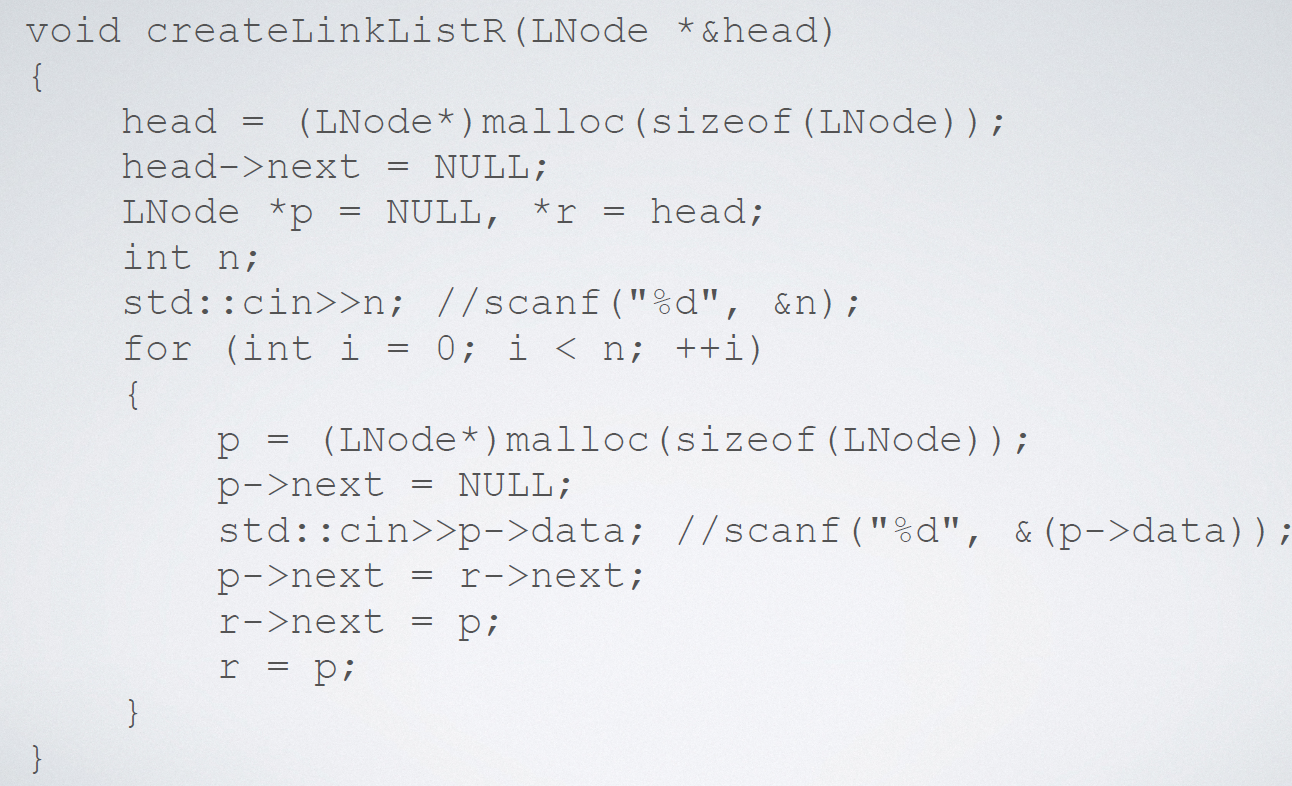
实现代码(头插法):
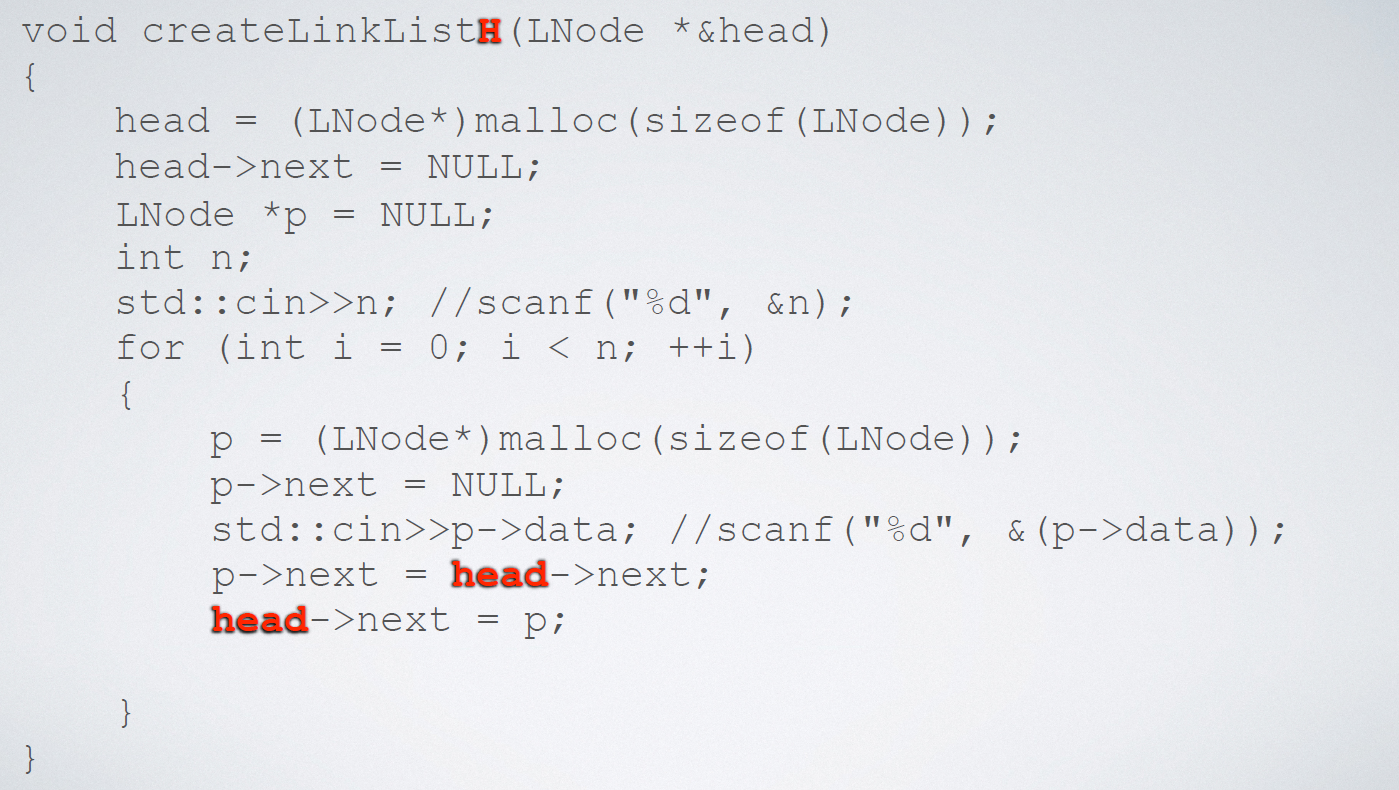
习题五:


2.7 逆置问题
2.7.1 顺序表逆置

主要实现代码:
for(int i = left,int j = right;i<j;++i,--j)
{
temp = a[i];
a[i] = a[j];
a[j] = temp;
}
2.7.2 链表逆置
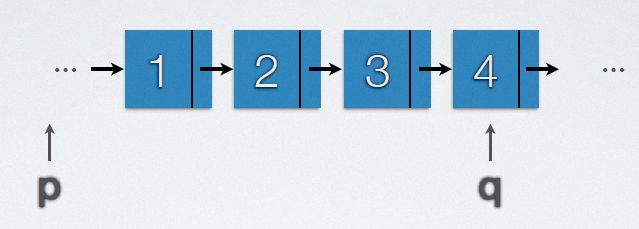
主要实现代码:
t = p->next;
p->next = t->next;
t->next = q->next;
q->next = t;
if(p->next ==q)
结束;
习题六:

1.算法思想,先将R中前P个元素逆置,再将剩下的元素逆置,最后将整个R逆置即可。
2.void reverse(int a[],int left,int right,int p)
{
for(int i = left,int j = right;i<left+p&&i<j;++i,--j)
{
temp = a[i];
a[i] = a[j];
a[j] = temp;
}
}
void solve(int a[],int n,int p)
{
reverse(a,0,p-1,p);
reverse(a,p,n-1,n-p);
reverse(a,0,n-1,n);
}
3.时间复杂度:O(n);
空间复杂度:O(1);
原地算法:辅助空间相对于输入数据量而言是个常数的算法
2.8 取最值
2.8.1 顺序表求最值
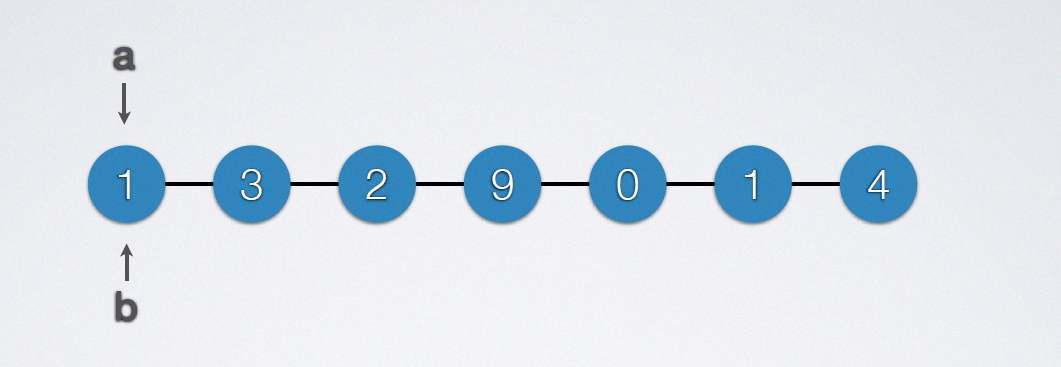
主要实现代码:
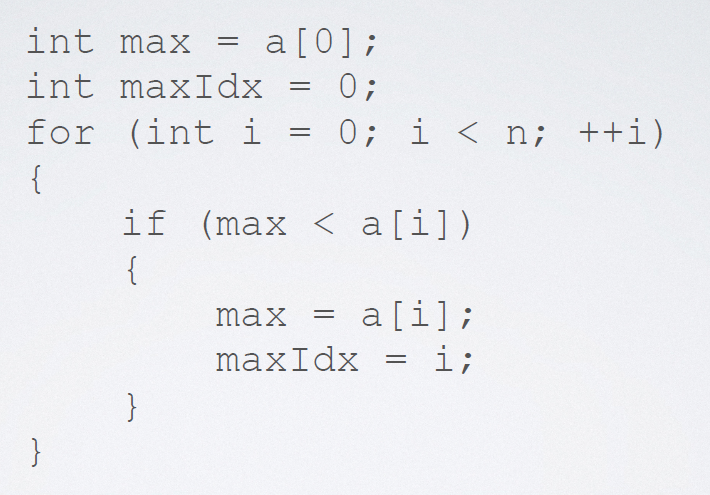
最小值改一下细节即可;
2.8.2 链表取最值
主要实现代码:
LNode *p,*q;
int max = head->next->data;
q = p = head->next;
while(p!=NULL)
{
if(max < p->data)
{
max = p->data;
q = p;
}
p = p->next;
}

习题七:

实现代码:
void maxFirst(DLNode *head)
{
## get max
DLNode *p = head->rlink,*q = p;
int max = p->data;
while(p!=NULL)
{
if(max<p->data)
{
max = p->data;
q = p;
}
p = p->rlink;
}
----------------------------------------
##delete
DLNode *l = q->llink,*r = q->rlink;
l->rlink = r;
if(r!=NULL)
r->llink = l;
----------------------------------------
##insert
q->llink = head;
q->rlink = head->rlink;
head->rlink = q;
q->rlink->llink = q;
}
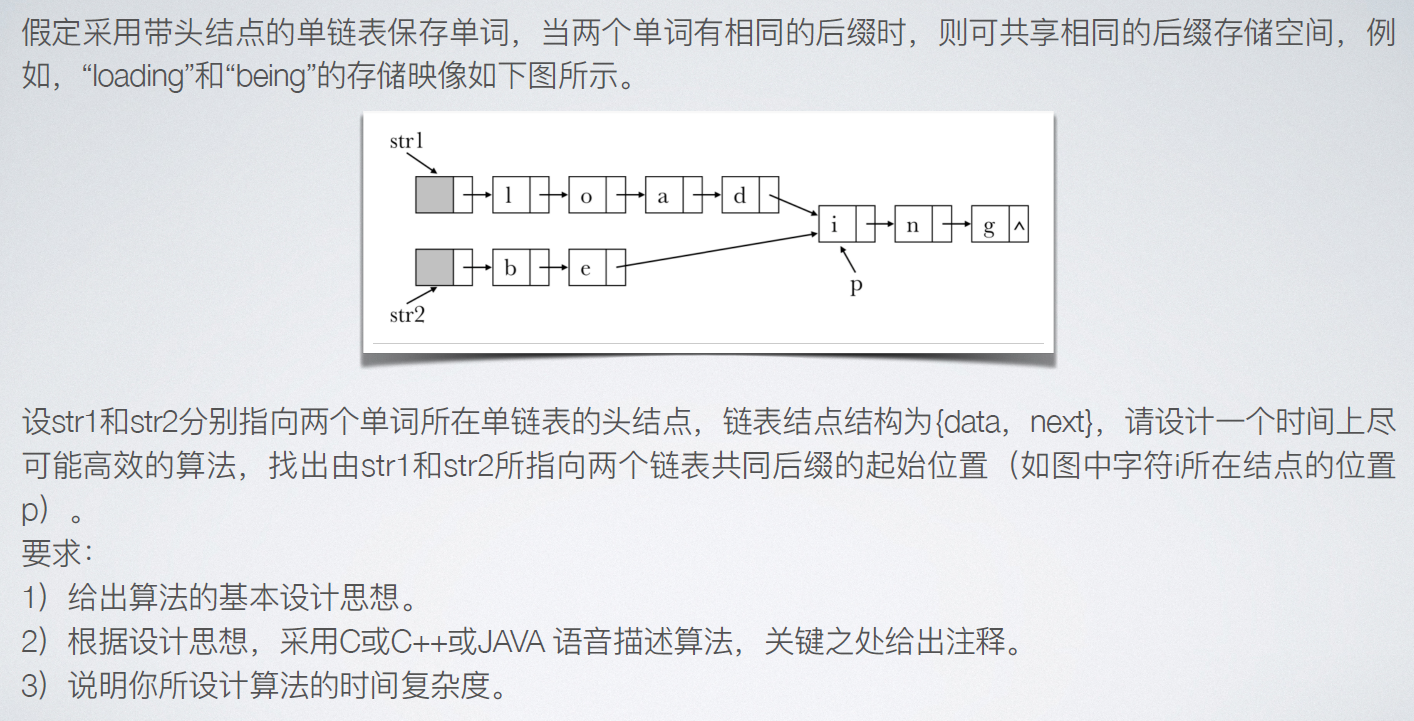
1.算法基本思想:
(1)分别求出两个链表的长度,len1,len2;
(2)令指针p、q分别指向str1和str2的头结点,若m>=n,则使p指向链表中的第m-n+1个结点;若m<n,则使q指向链表中的第n-m+1个结点;即使指针p和q所指的结点到表尾的长度相等。
(3)将指针p和q同步向后移动,并判断它们是否指向同一结点。若p和q指向同一结点,则该点即为所求的共同后缀的起始位置。
2.LNode *solve(LNode *str1,LNode *str2)
{
int len1 = 0,len2 = 0;
LNode *p = str1->next,*q = str2->next;
while(p!=NULL)
{
len1++;
p = p->next;
}
while(q!=NULL)
{
len2++;
q = q->next;
}
for(p = str1->next;len1>len2;len1--)
p = p->next;
for(q = str2->next;len1<len2;len2--)
q = q->next;
while(p!=NULL&&p!=q)
{
p = p->next;
q = q->next;
}
return p;
}
3.时间复杂度为O(n)
2.9 划分
给一个顺序表,以第一个元素为枢轴,使左面的元素都小于枢轴,右面的元素都大于枢轴
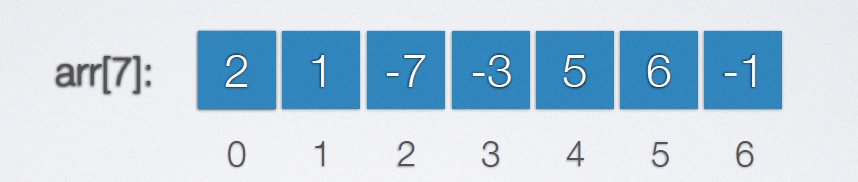
思想:
首先定义一个temp常量 ,将枢轴赋值给temp,然后定义数组两端位置i,j,i<j,左移j扫描,如果扫到比枢轴小的数字就把他移动到i位置,然后i右移,如果找到比枢轴大的元素就把他移动到j位置
实现代码:
void partition(int arr[],int n)
{
int temp;
int i = 0,j = n-1;
temp = arr[i];
while(i<j)
{
while(i<j&&arr[j]>=temp)
--j;
if(i<j)
{
arr[i] = arr[j]
++i;
}
while(i<j&&arr[i]<temp)
++i;
if(i<j)
{
arr[j] = arr[i]
--j;
}
}
arr[i] = temp;
}
效果是把数组元素以Y为界限分成了前后两部分,前半部分小于Y,后半部分大于等于Y;
i和j最终指向的值是X,而不是Y。
习题八:
有一个线性表,采用带头结点的单链表L来存储。设计一个算法将其逆置。要求不能建立新结点,只能通过表中已有结点的重新组合来完成。
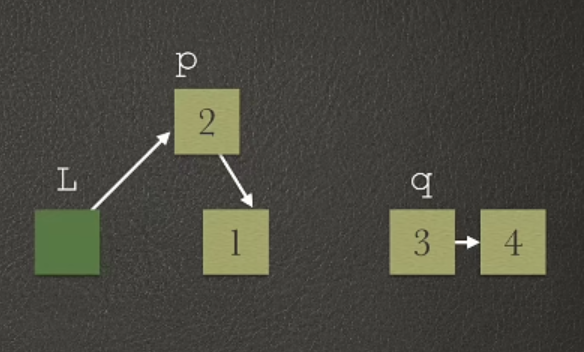
实现代码:
LNode *p = head->next,*q;
L->next = NULL;
while(p!=NULL)
{
q = p->next;
p->next = L->next;
L->next = p;
p = q;
}
写一个函数,逆序打印单链表中的数据,假设指针L指向了单链表的开始结点.
实现代码:
void reprint (LNode *L)
{
if(L!=NULL)
{
reprint(L->next);
cout<<L->data<<" ";
}
}
2.10 归并
2.10.1 顺序表归并
实现代码:
void mergearray(int a[],int m,int b[],int n,int c[])
{
int i,j = 0;
int k = 0;
while(i < m&&j<n)
{
if(a[i]<b[j])
c[k++] = a[i++];
else
c[k++] = b[j++];
}
while(i<m)
c[k++] = a[i++];
while(j<n)
c[k++] = b[j++];
}
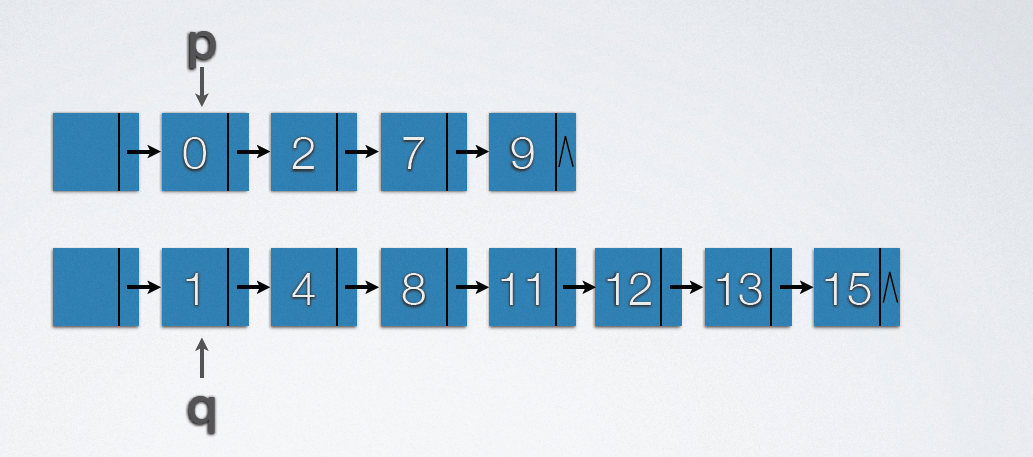
2.10.2 链表归并

实现代码(尾插法):
void merge(LNode *A,LNode *B,LNode *&C)
{
LNode *p = A->next;
LNode *q = B->next;
LNode *r;
C = A;
C->next = NULL;
free(B);
r = C;
while(p!= NULL&&q!=NULL)
{
if(p->data<=q->data)
r->next = p; p = p->next;
r = r->next;
else
r->next = q; q = q->next;
r = r->next;
}
if(p!=NULL)
r->next = p;
if(q!=NULL)
r->next = q;
}
实现代码(头插法):逆序归并
void mergeR(LNode *A,LNode *B,LNode *&C)
{
LNode *p = A->next;
LNode *q = B->next;
LNode *s;
C = A;
C->next = NULL;
free(B);
while(p!= NULL&&q!=NULL)
{
if(p->data<=q->data)
s = p;p = p->next;
s->next = C->next;
C->next = s;
else
s = q;q = q->next;
s->next = C->next;
C->next = s;
}
while(p!=NULL)
s = q;q = q->next;
s->next = C->next;
C->next = s;
while(q!=NULL)
s = q;q = q->next;
s->next = C->next;
C->next = s;
}