一、二叉树概念
二叉树是树的一种,二叉树中的结点至多只能有两个子结点。二叉树的根结点下可分成两个子树,称为左子树和右子树,左子树和右子树亦称二叉树。
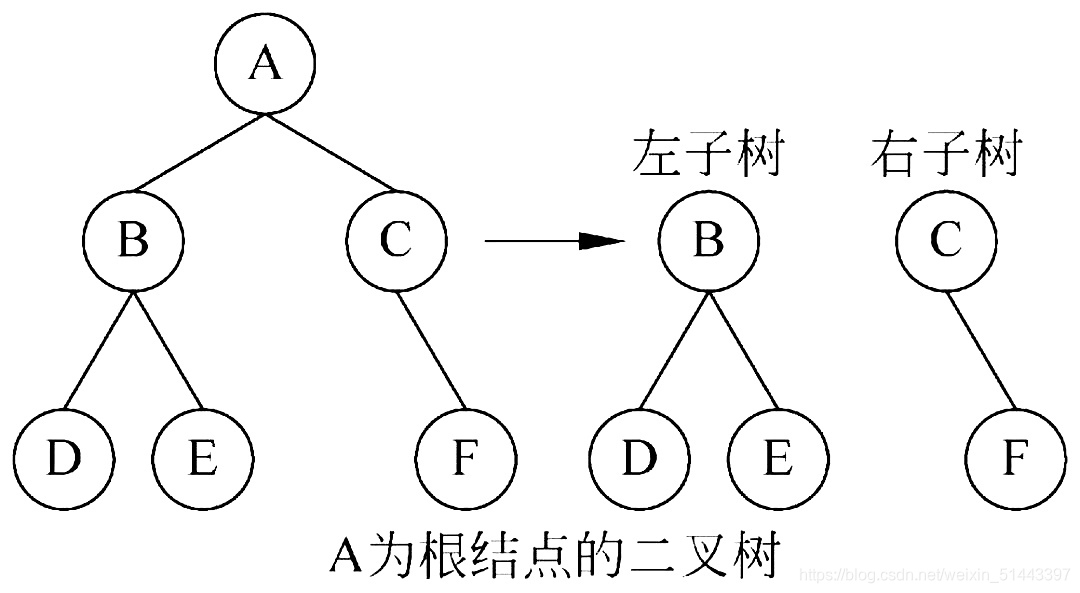
二、存储结构
struct node
{
int value;//结点的值
node *l,*r;//左右子结点
};
三、二叉树的遍历
先序遍历:父节点,左儿子,右儿子
中序遍历:左儿子,父节点,右儿子
后序遍历:左儿子,右儿子,父节点
例:输入二叉树的先序和中序遍历序列,求后序遍历。模板题:
#include <iostream>
#include <cstdio>
using namespace std;
const int N=1010;
int pre[N],in[N],post[N];
int k;
struct node
{
int value;//结点的值
node *l,*r;//左右结点
node(int value=0,node *l=NULL,node *r=NULL):value(value),l(l),r(r) {}
};
void buildtree(int l,int r,int &t,node* &root)//建树
{
int flag=-1;
for(int i=1; i<=r; i++)
{
if(in[i]==pre[t])
{
flag=i;//记录根在中序的位置
break;
}
}
if(flag==-1)
return;
root=new node(in[flag]);//新建结点
t++;
if(flag>l)
buildtree(l,flag-1,t,root->l);
if(flag<r)
buildtree(flag+1,r,t,root->r);
}
void preorder(node * root)//求先序序列
{
if(root!=NULL)
{
post[k++]=root->value;//输出
preorder(root->l);
preorder(root->r);
}
}
void inorder(node * root)//求中序序列
{
if(root!=NULL)
{
inorder(root->l);
post[k++]=root->value;//输出
inorder(root->r);
}
}
void postorder(node * root)//求后序序列
{
if(root!=NULL)
{
postorder(root->l);
postorder(root->r);
post[k++]=root->value;//输出
}
}
void remove_tree(node * root)
{
if(root==NULL)
return;
remove_tree(root->l);
remove_tree(root->r);
delete root;
}
int main()
{
int n;
while(~scanf("%d",&n))
{
for(int i=1; i<=n; i++)
{
scanf("%d",&pre[i]);
}
for(int j=1; j<=n; j++)
{
scanf("%d",&in[j]);
}
node * root;
int t=1;
buildtree(1,n,t,root);
k=0;//记录结点个数
postorder(root);
for(int i=0; i<k; i++)
{
printf("%d %c",post[i],i==k-1?'\n':' ');
}
remove_tree(root);
}
return 0;
}
四、二叉树搜索树BFS
1.特征
?每个元素有唯一键值在BFS节点上
?任意一个结点的键值,比他左子树的所有结点的键值大,比他右子树所有结点的键值小。
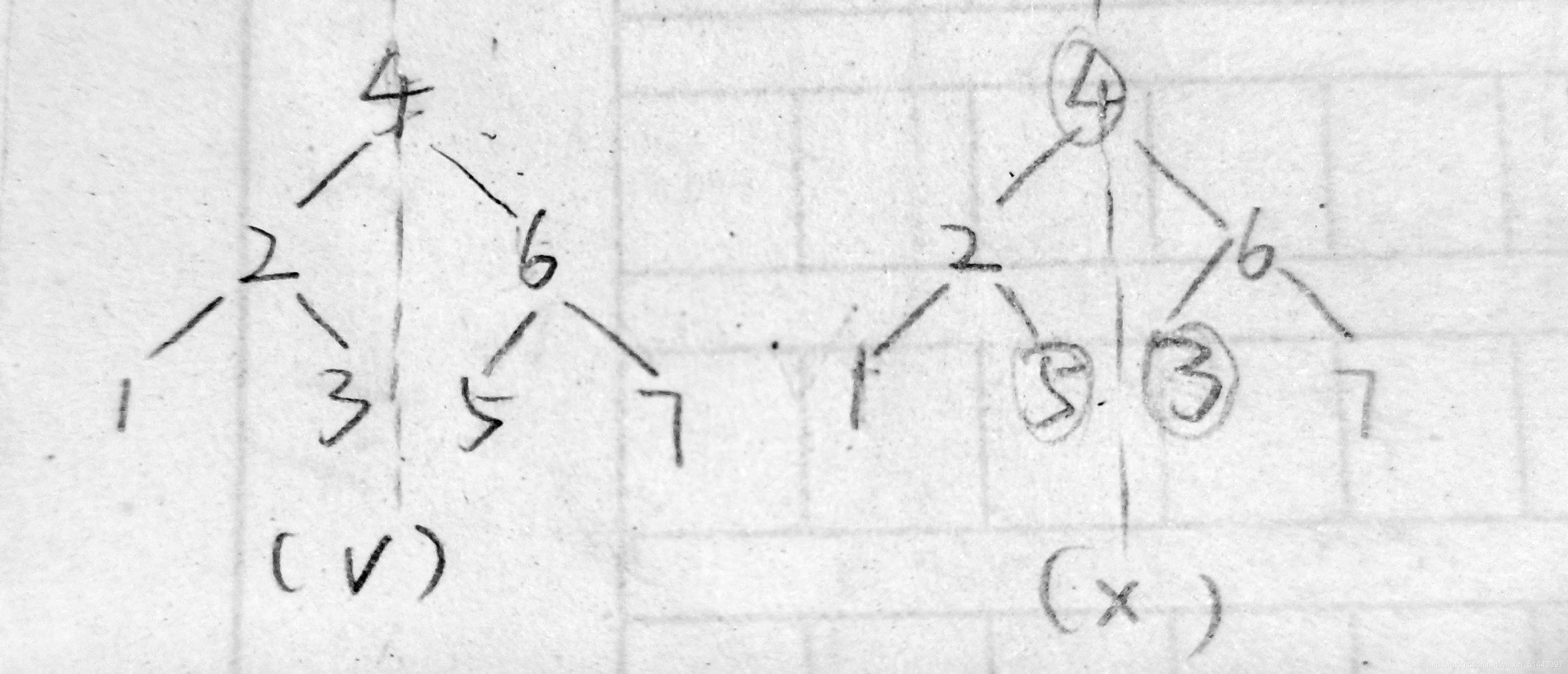
2.实现方式:
?建树和插入?查询?删除?遍历
例:The order of a Tree
题意:由n个数构成一棵二叉搜索树,寻找字典序最小的插入顺序,构成一棵相同的树。
初学小白,简单题也做好久,T_T。
题例:1 3 4 2
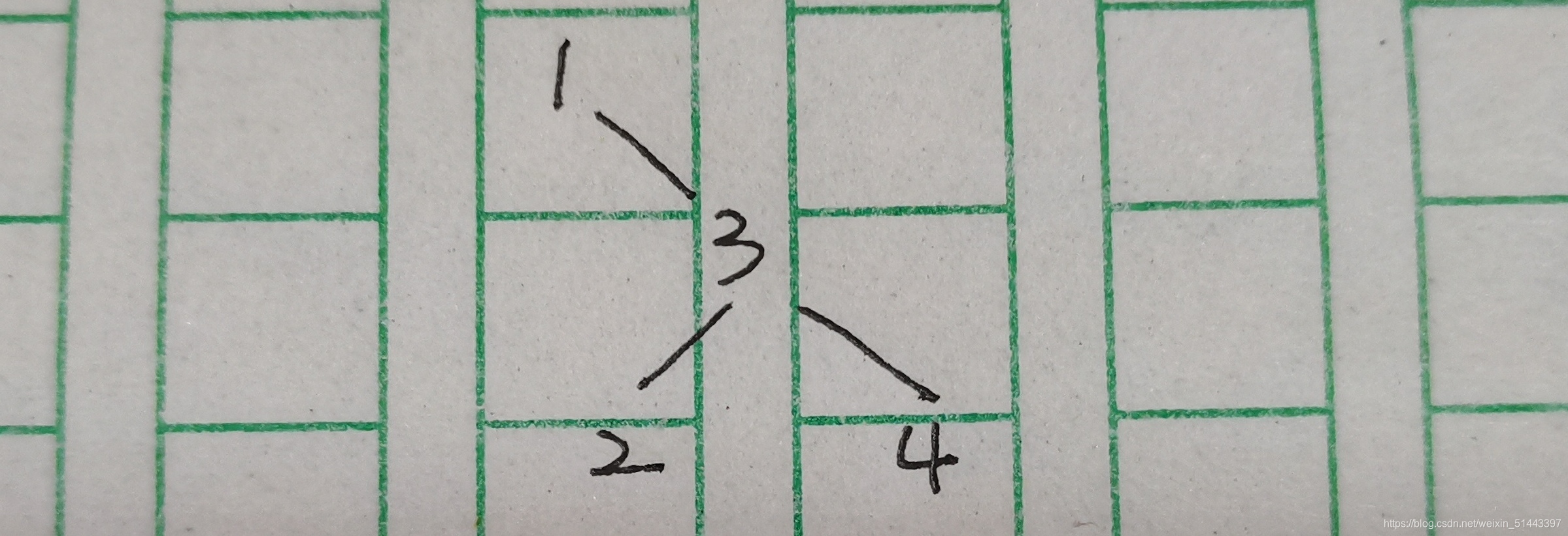
先序:1 3 2 4(同树,字典序最小)
中序:1 2 3 4(不同树)
后序:2 4 3 1(不同树)
层次遍历:1 3 2 4(同树,字典序最小)
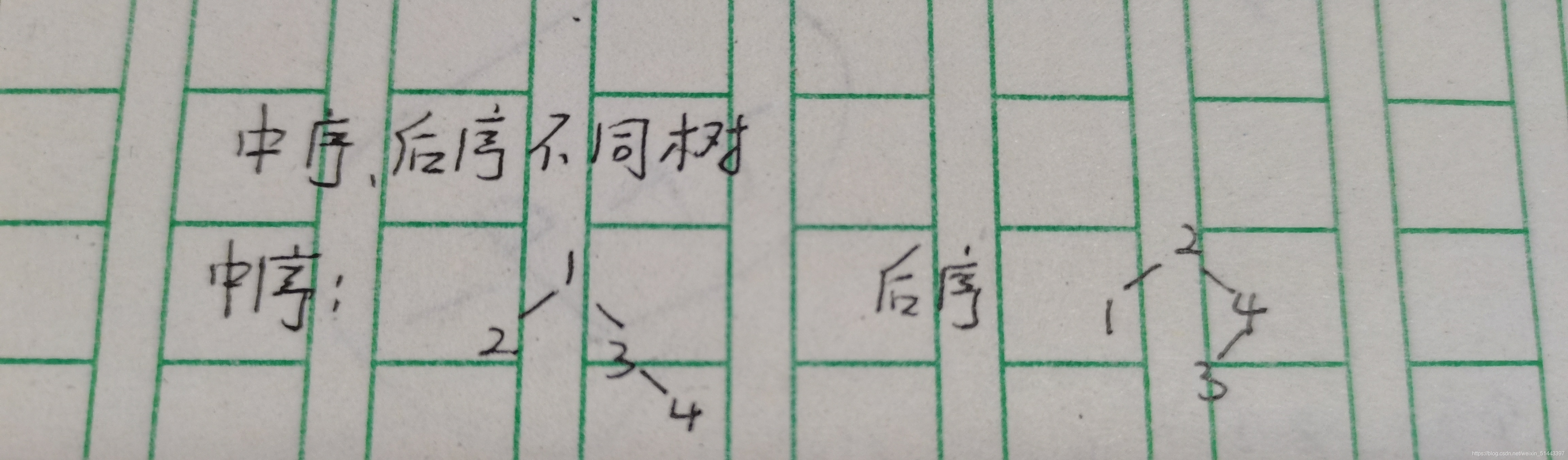
发现这里先序和层次遍历结果一样了,再换一个其他例子。
如:4 6 5 2 7 1 3
先序:4 2 1 3 6 5 7(同树,字典序最小)
中序:1 2 3 4 5 6 7(不同树)
后序:1 3 2 5 7 6 4(不同树)
层次:4 2 6 1 3 5 7(同树,字典序不最小)
多举几个例子,发现先序遍历符合字典序最小且树不变的情况。
#include <iostream>
#include <cstdio>
using namespace std;
const int N=1e5+5;
int pre[N],k;
struct node
{
int value;//结点的值
node *l,*r;//左右结点
};
void add(node* &root,int &t)//插入
{
//t表示插入的价值
if(root==NULL)
{
root=new node;//新建结点
root->value=t;
root->l=root->r=NULL;
}
else
{
if(t>root->value)
add(root->r,t);
else add(root->l,t);
}
}
void preorder(node * root)//求先序序列
{
if(root!=NULL)
{
pre[k++]=root->value;//输出
preorder(root->l);
preorder(root->r);
}
}
void remove_tree(node * root)
{
if(root==NULL)
return;
remove_tree(root->l);
remove_tree(root->r);
delete root;
}
int main()
{
int n;
while(cin>>n)
{
node * root=NULL;
int x;
for(int i=1; i<=n; i++)
{
cin>>x;
add(root,x);
}
k=0;
preorder(root);
for(int i=0; i<k; i++)
{
printf("%d%c",pre[i],i==k-1?'\n':' ');
}
remove_tree(root);
}
return 0;
}
void add(node* &root,int &t)关于这里的写法,node * &root中的&不能省去,传入的是存储指针的地址。
一般用指针做函数形参是为了传入参数地址,来进行修改实参数的值,即指针指向的值。但是如果要用来修改指针本身的值则需要指针的指针或者指针变量的传址引用。
(目前也不是很懂,参考其他博主)