[数据结构与算法]Math(牛客多校第三场)

Math

题意：

问你有多少对(x,y),1<=x<=y<=n,满足(x² + y²)%(xy+1) == 0

题解：

这种题。。。直接打表芜湖~

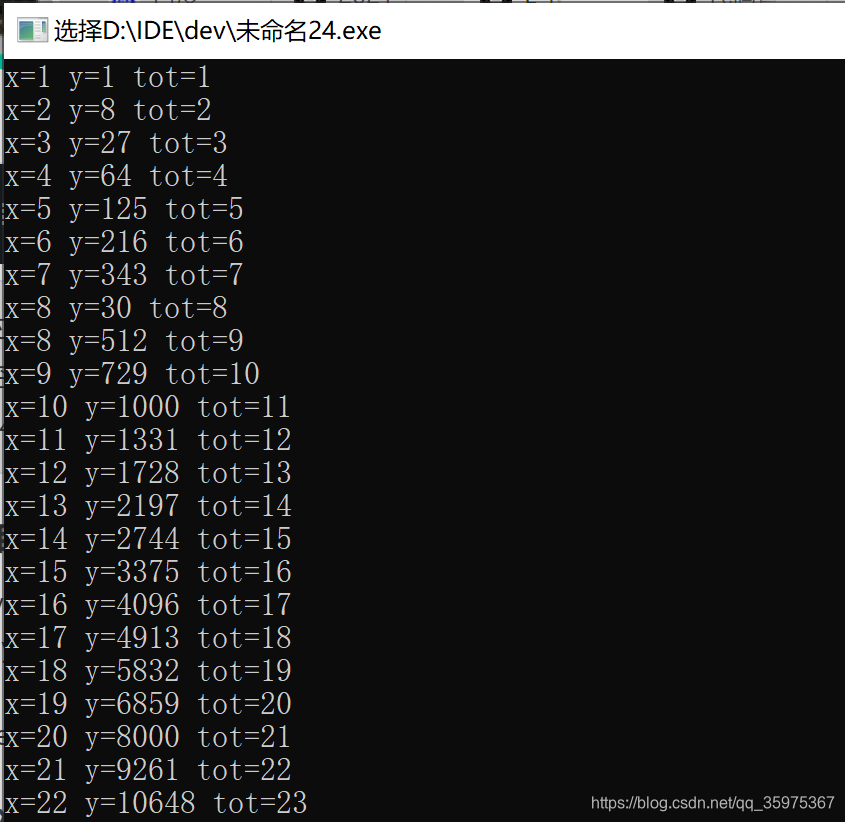
通过打表发现：满足情况的为(i,i * i * i),但是也有不和谐的声音出现：当x=8时，会出现两个，一个是(8,30),另一个是(8,512)，后者依然满足规律，所以前者有问题，完美继续找发现27也是，不满足的是(27,240),再往下发现有(30,112),再往下看会发现，不满足规律的情况其实是很多条链：
(8,30)(30,112)（112，418）…
(27,240)（240，）…
(64,1020)(1020, )…
我们发现这些数很多是相连的，而不想连的数彼此之间开头都是i * i * i，再通过枚举几个总结规律，每个链的开始都是a=i * i * i,后面紧跟着是(a * i * i )-pre,pre是上一组

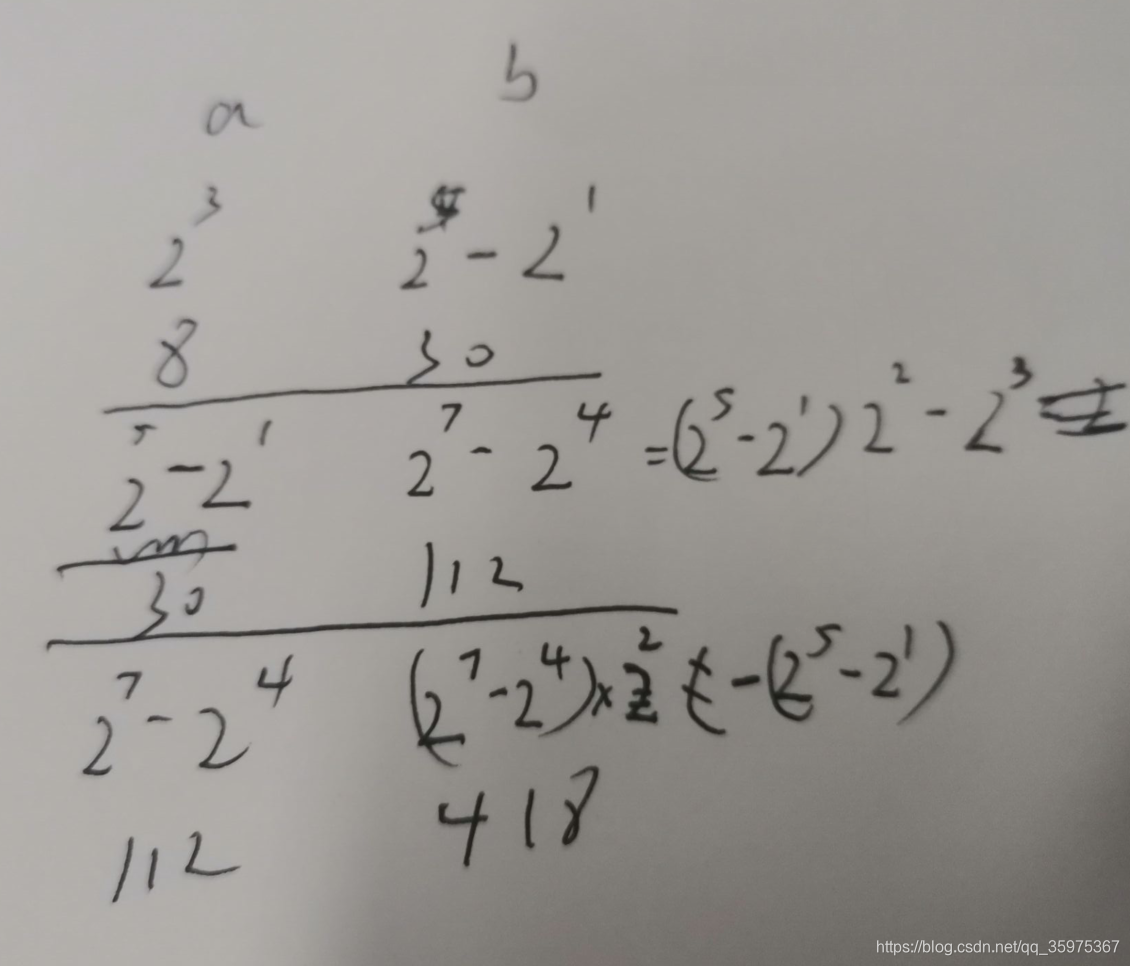
找到规律，我们预处理出所有情况，然后排序，找到每个情况的上限值，直接二分就行

代码：

#include<bits/stdc++.h>
#define debug(a,b) printf("%s = %d\n",a,b);
typedef long double ll;
using namespace std;
//Fe~Jozky
const ll INF=0x3f3f3f3f;
inline int read(){
   int s=0,w=1;
   char ch=getchar();
   while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
   while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();//s=(s<<3)+(s<<1)+(ch^48);
   return s*w;
}
ll inf=1e18;
const int N=1e6;
long double a[7000007];
int tot=0;
void init(){
	for(int i=2;i<=N;i++){
		ll x=1ll*i*i*i;
		a[++tot]=x;
		ll t=x*i*i-i;
		if(t>inf)continue;
		ll prea=x;
		while(t<inf){
			a[++tot]=t;
			t=1ll*t*i*i-prea;
			prea=a[tot];
		}
	}
	sort(a+1,a+1+tot);
}
int main()
{
    init();
    int t=read();
    while(t--){
    	long double x;
    	cin>>x;
    	int id=lower_bound(a+1,a+1+tot,x)-a;
    	if(a[id]>x)id--;
    	cout<<id+1<<endl;
	}
	return 0;
}