南昌理工学院acm集训队
为什么要用到线段树这个算法?
举个简单的例子:
当我们有一段已知的数组 a 的时候
想要得到一段区间[l,r]的和,可以通过前缀和O(1)的时间把他算出来,但是如果想要修改a[idx]的值的时候,却要用到O(n)的时间复杂度。
同样,如果不用前缀和,修改的时间复杂度是O(1),而求区间和的时间复杂度又变为O(n)。
所以线段树的作用就是,维护一个数组,无论进行什么操作,时间复杂度都可以降到为O(logn)
线段树的构建
线段树其实就是一颗二叉树,用图可以表示为(不要嫌丑,真的画了好久,画的我好难过 )
原数组为 arr 的一颗二叉树,L为该节点的左儿子节点,R为该节点的右儿子节点,SUM为该节点的权值
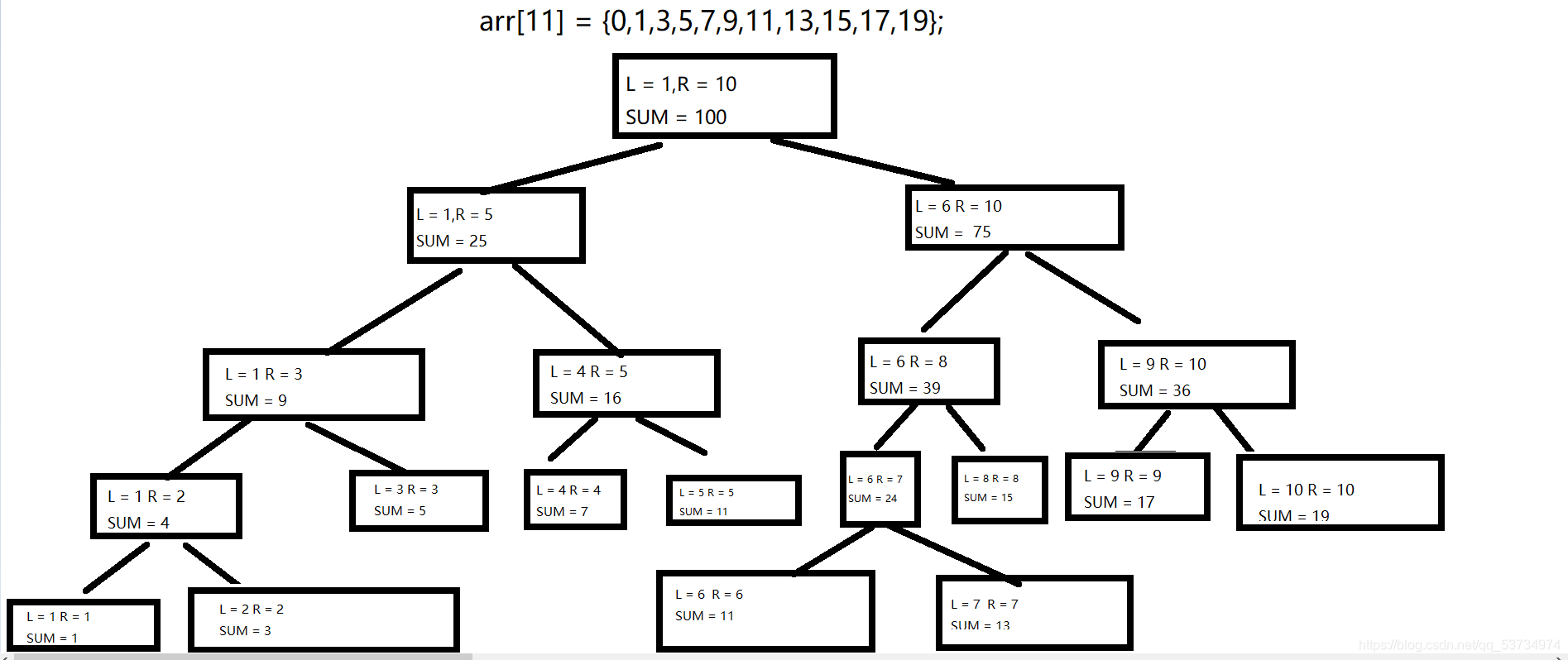
结合图中,我们可以发现:
当且仅当节点为叶子节点,也就是L = R的时候,该节点的权值就等于原数组arr[L]的权值,而当L != R的时候,该节点的权值就等于左儿子节点的权值和右儿子节点的权值之和,并且每次都是通过折半的方式去找左右儿子,知道不能折半找为止
有了这些知识,就可以根据这些写出构建一颗线段树的代码
(含注释)
int arr[11] = {0,1,3,5,7,9,11,13,15,17,19};
//用一个结构体存储一颗线段树,L为左儿子节点,R为右儿子节点,SUM为该节点的权值
struct Node{
int l,r;
int sum;
}tree[N];
void build_tree(int i,int l,int r)
{
tree[i].l = l; tree[i].r = r; //将左儿子右儿子赋给他的父亲节点
if(l == r)//如果该点为叶子节点
{
tree[i].sum = arr[l];
return;
}
int mid = l + r >> 1;//对半生根
build_tree(i * 2,l,mid);//建立左儿子
build_tree(i * 2 + 1,mid + 1,r);//建立右儿子
//该点权值等于递归结束后左右儿子权值相加
tree[i].sum = tree[i * 2].sum + tree[i * 2 + 1].sum;
}
int main()
{
build_tree(1,1,n);//n为数组的大小
}
线段树的功能
1. 修改数组的任意一个值
同样,我们想要修改一个值的时候,首先要找到他的叶子节点,然后将他的值进行修改,并且在改之后,再递归使用
tree[i].sum = tree[i * 2].sum + tree[i * 2 + 1].sum;
来更新他父亲与祖宗节点的权值
例如我们要将arr[4]从原来的7改为6,递归过程为
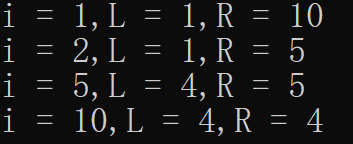
从图中可以看到,从祖宗节点开始,依次查询idx在哪个区间里,不断地往下找,直到找到叶子节点为止
所以每次找的时候都有
if(idx <= tree[node * 2].r) //idx处于该结点的左儿子中 向左找
{
update_tree(node * 2,idx,val);
}
else //idx处于该节点的右儿子中,向右找
{
update_tree(node * 2 + 1,idx,val);
}
在每次递归完之后,再进行一次权值更新
所以完整代码为
void update_tree(int i,int idx,int val)
{
if(tree[i].l == tree[i].r)
{
tree[i].sum = val;
return;
}
if(idx <= tree[i * 2].r)
{
update_tree(i * 2,idx,val);
}
else
{
update_tree(i * 2 + 1,idx,val);
}
tree[i].sum = tree[i * 2].sum + tree[i * 2 + 1].sum;//更新权值
}
2.查询树中任意区间[l,r]的和
例如我们要查询区间[3,7]的和,由图可知,我们要得到几个叶子节点的值。但是这一步可以优化为[3,3],[4,5],[6,7]这三个区间的和,因为[4,5]这个区间的权值就是包含[4,4],[5,5]这两个叶子节点的权值之和,[6,7]区间也是如此
所以这一步,可以用代码表示为
//如果要求的区间完全包含于该区间
if(tree[i].r <= R && tree[i].l >= L)
{
return tree[i].sum;
}
而找区间的时候,如果要找的区间有存在与左儿子中,那么便要向左边去找,如果要找的区间有存在于右儿子中,那么便要向右边找
代码可以表示为
int s = 0;
if(tree[i * 2].r >= L) s += query_tree(i * 2,L,R);
if(tree[i * 2 + 1].l <= R) s += query_tree(i * 2 + 1,L,R);
return s;
}
递归过程为
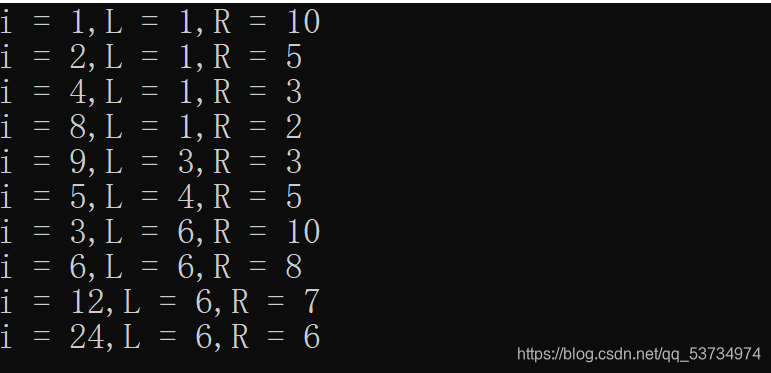
所以完整代码为
int query_tree(int i,int L,int R)
{
if(tree[i].r <= R && tree[i].l >= L)
{
return tree[i].sum;
}
if(R < tree[i].l || tree[i].r < L) //如果要找寻的区间完全不存在与左儿子和右儿子之中
{
return 0;
}
int s = 0;
if(tree[i].r >= L) s += query_tree(i * 2,L,R);
if(tree[i * 2 + 1].l <= R) s += query_tree(i * 2 + 1,L,R);
return s;
}
如果你已经完全掌握了上述,可以将洛谷的该题默写出来了,就可以继续往下学习了。
树状数组1