[数据结构与算法]做题记录2021.7.24

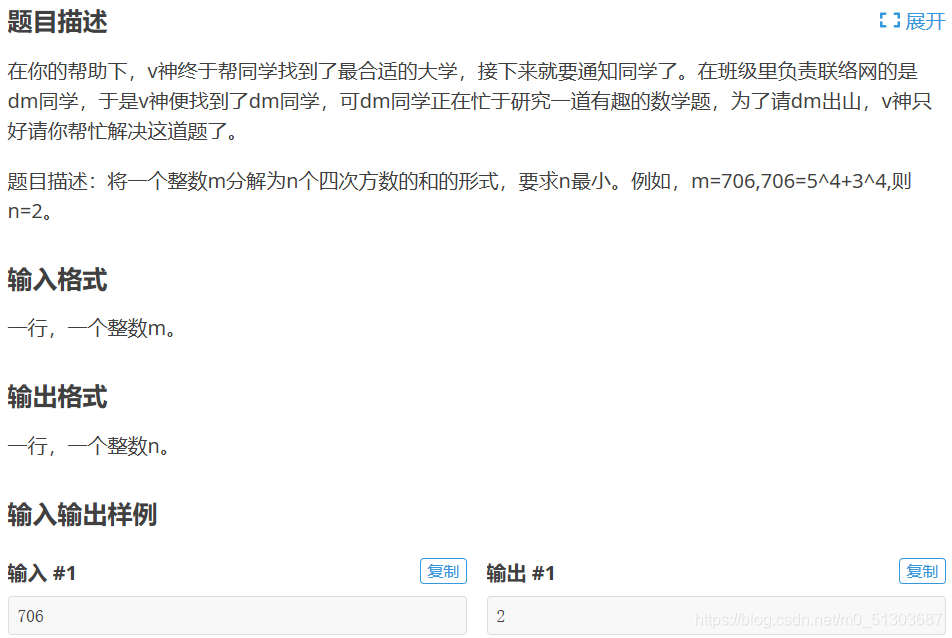
乍一看，这题用贪心好像没什么问题，每次我们都找最大的t使t⁴<=m，并不断更新m.
然而：

一开始也不知道为什么，后来明白了。如果按照这个思路，那么选到后面的数字减到0的次数反而会更多，也就是说，局部最优不一定导致全局最优。
然后就想用记忆化搜索，但发现数据过大会MLE（可能是我的策略有问题？），于是使用动态规划。
定义dp[i]：数字i按题意分解所需的最少项，我们有：
dp[i]=min{dp[i-t⁴]}，t>=0且t⁴<=i
按以上递推式写出代码：

#include <cstdio>
#include <algorithm>
#include <cmath>
const int M=100001; 
using namespace std;
int dp[M];

int main(){
    int m;
    scanf("%d",&m);
    fill(dp+1,dp+m+1,M);
    dp[0]=0;
	for(int i=1; i<=m; i++) {
    	for(int j=1; (int)pow(j,4)<=i; j++) {
    		dp[i]=min(dp[i],dp[i-(int)pow(j,4)]+1);
		}
	}
    printf("%d",dp[m]);
    return 0;
}

就可以AC了
此题也可按照完全背包的思路，设每个“物品”i价值为1，重量为i⁴，“物品”个数为[m^1/4]+1，“背包”容量为m即可。