[数据结构与算法]（五）图论模型

一、Dijkstra算法

Dijkstra算法可用于求解图中某源点到其余各顶点的最短路径

理论部分

算法实现步骤：
① 每次找出当前图中距离源点1最近的点k，
② 计算源点1经过该点k到达某个点j是否比原来更近，如果更近，则把源点1到某个点j的距离，替换为这个更近的距离。
③ 经过n-1次查找（把除了源点之外的点都遍历一遍，每个点都当一次中介值），即可得出源点到每个点最近的距离。

?

# -*- coding: utf-8 -*-

def get_shortest_route(mgraph):
    n = len(mgraph)       # 顶点个数
    dp = [float('inf')]*n # 一维数组保存到各点的最短距离
    dpp = [[]]*n          # 二维数组保存到各点的最短距离的路径
    seen = [0]*n          # 一维数组记录各顶点是否访问
    
    # 到各点的初始化最短距离
    for i in range(n):
        dp[i] = mgraph[0][i]
        dpp[i] = [i+1]
    print('到各点的初始化最短距离：', dp)
    
    # n-1次查找
    for i in range(1, n):
        min_ = float('inf')
        # 当前图中距离源点1最近的点k
        for j in range(1, n):
            if dp[j] < min_ and seen[j] == 0:
                min_ = dp[j]
                k = j
        
        seen[k] = 1
        #  计算点1经过点k到达某个点j是否比原来更近
        for j in range(1, n):
            if dp[j] > dp[k]+mgraph[k][j] and seen[j] == 0:
                dp[j] = dp[k]+mgraph[k][j]
                dpp[j] = [k+1, j+1]
    return dp, dpp


if __name__ == "__main__":
    inf = float('inf')
    mgraph = [[0, 5, 2, inf, inf],
              [inf, 0, 2, 6, 1],
              [inf, inf, 0, 7, 6],
              [inf, inf, 7, 0, 2],
              [inf, inf, inf, inf, 0]]
    dp, dpp = get_shortest_route(mgraph)
    for i in range(len(dp)):
        print('到点', i+1 ,'的最短距离：',dp[i],'路径：', dpp[i])


运行结果：
runfile('E:/Dijkstra.py', wdir='E:/')
到各点的初始化最短距离： [0, 5, 2, inf, inf]
到点 1 的最短距离： 0 路径： [1]
到点 2 的最短距离： 5 路径： [2]
到点 3 的最短距离： 2 路径： [3]
到点 4 的最短距离： 9 路径： [3, 4]
到点 5 的最短距离： 6 路径： [2, 5]

二、Floyd算法

它的理念跟Dijkstra有点不一样，但是最终的结果是一样的。Floyd算法主要是用到了动态规划的思想。求解出任意两点的最短路径及其距离。

整个算法的思想就是：最开始只允许经过1号顶点进行中转，接下来只允许经过1和2号顶点进行中转，接下来······，到允许经过1~n号所有顶点进行中转，求任意两点之间的最短路程。用一句话概括就是：从i号顶点到j号顶点只经过前k号点的最短路程。

graph = {'A': [(7, 'A', 'B'), (5, 'A', 'D')], 
         'B': [(7, 'B', 'A'), (8, 'B', 'C'), (9, 'B', 'D'), (7, 'B', 'E')], 
         'C': [(8, 'C', 'B'), (5, 'C', 'E')],
         'D': [(5, 'D', 'A'), (9, 'D', 'B'), (15, 'D', 'E'), (6, 'D', 'F')], 
         'E': [(7, 'E', 'B'), (5, 'E', 'C'), (15, 'E', 'D'), (8, 'E', 'F'), (9, 'E', 'G')], 
         'F': [(6, 'F', 'D'), (8, 'F', 'E'), (11, 'F', 'G')],
         'G': [(9, 'G', 'E'), (11, 'G', 'F')]
        }
def graph2adjacent_matrix(graph):
    vnum = len(graph)
    dict = {'A':0,'B':1,'C':2,'D':3,'E':4,'F':5,'G':6}
    adjacent_matrix = [[0 if row==col else float('inf') for col in range(vnum)] for row in range(vnum)]
    vertices = graph.keys()
    for vertex in vertices:
        for edge in graph[vertex]:
            w,u,v = edge
            adjacent_matrix[dict.get(u)][dict.get(v)]=w
    return adjacent_matrix

def floyd(adjacent_matrix):
    vnum = len(adjacent_matrix)
    a = [[adjacent_matrix[row][col] for col in range(vnum)] for row in range(vnum)]
    nvertex = [[-1 if adjacent_matrix[row][col]==float('inf') else col for col in range(vnum)] for row in range(vnum)]
    # print(adjacent_matrix)
    for k in range(vnum):
        for i in range(vnum):
            for j in range(vnum):
                if a[i][j]>a[i][k]+a[k][j]:
                    a[i][j]=a[i][k]+a[k][j] 
                    nvertex[i][j] = nvertex[i][k]
    return nvertex, a

adjacent_matrix = graph2adjacent_matrix(graph)
nvertex, a = floyd(adjacent_matrix)
### 打印原邻接矩阵 ###
for i in range(len(adjacent_matrix)):
    for j in range(len(adjacent_matrix[0])):
        print(adjacent_matrix[i][j],end="\t")
    print()#打印一行后换行
### 打印经过的顶点 ###
print()
for i in range(len(nvertex)):
    for j in range(len(nvertex[0])):
        print(nvertex[i][j],end="\t")
    print()#打印一行后换行
### 打印彼此之间的最短距离 ###
print()
for i in range(len(a)):
    for j in range(len(a[0])):
        print(a[i][j],end="\t")
    print()#打印一行后换行

?

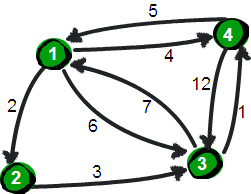
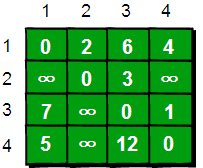
比如1号城市到2号城市的路程为2，则设A(1, 2)的值为2。2号城市无法到达4号城市，则设置A(2, 4)的值为∞

。另外此处约定一个城市自己是到自己的也是0，例如A(1, 1)为0。