前言
前两篇文章中我们学习了线性表中的数组和链表,数组和链表是最基础的数据结构,很多数据结构的实现都是基于数据或链表的。那么今天我们一起学习一个非常简单的数据结构—栈。栈使用是非常广泛的,比如我们Java中函数的调用、浏览器中的前进与后退功能等都会用到栈。
什么是栈
先画张图,看看栈长什么样。如下图所示:
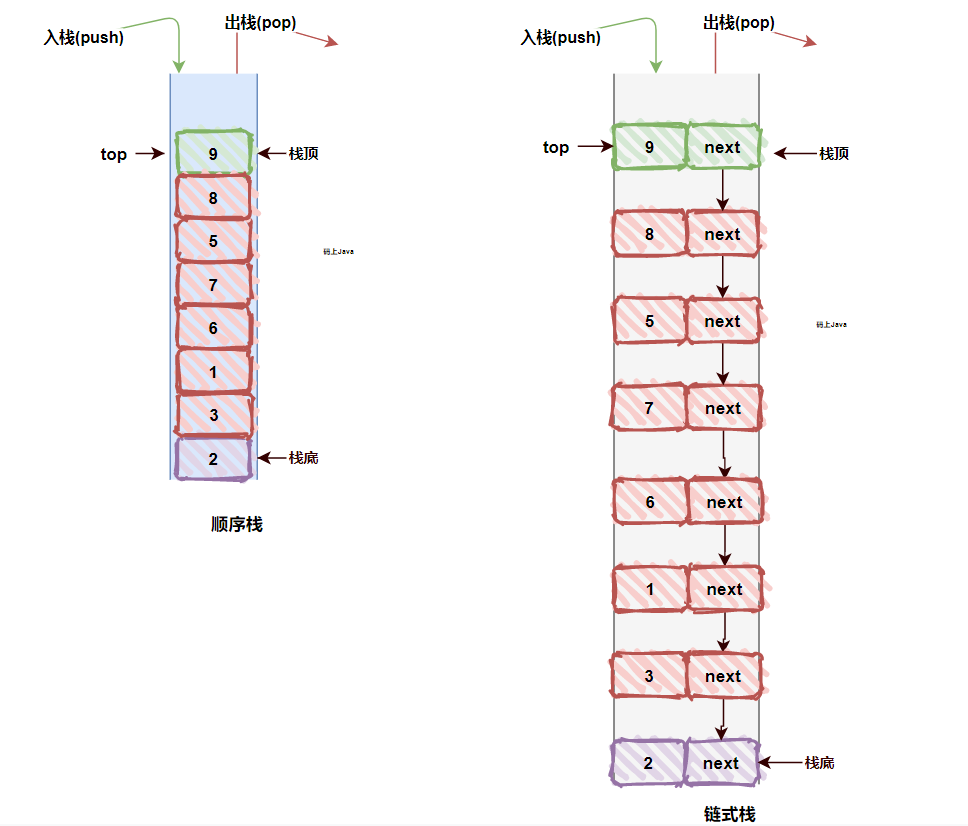
从图中看到栈是有些特殊,对于栈的操作被限制只能在栈的一端(栈顶)进行,也就是不允许在栈的中间进行数据操作,只能在栈顶进行数据操作(也就是插入和删除数据)。
思考:“受限制”的栈有什么用呢?
特定的数据结构肯定有其特定的使用场景,相比于数组或者链表而言,栈虽然没有怎么灵活(只能在栈的一端进行数据操作),但是对于新增或者删除数据的时候,因为栈只涉及到一端,效率肯定不低。
如何去理解栈呢?其实也非常简单,一句话可以概况栈的特性:先进后出,俗称“吃多了吐”。哈哈~
栈的基本操作
栈有不同的实现方式,基于数组实现的栈,被叫做顺序栈。基于链表实现的栈,被叫做链式栈。不管用什么方式实现的栈,其原理都是一样的,不用担心!
栈的操作主要就两个:入栈(push)和出栈(pop)。
- 顺序栈
下面我们先基于数组来实现一个顺序栈,代码如下:
public class MyStack<E> {
private Object[] data = null; // 数组
private int maxSize = 0; //栈容量
private int top = -1; //栈顶指针
// 初始化构造方法
MyStack(int initialSize) {
if (initialSize >= 0) {
this.maxSize = initialSize;
data = new Object[initialSize];
top = -1;
} else {
throw new RuntimeException("初始化大小不能小于0: " + initialSize);
}
}
// 初始化构造方法 默认栈容量为10
public MyStack() {
this(10);
}
//入栈操作
public boolean push(E e) {
//首先判断一下栈是否已经满了
if (top == maxSize - 1) {
// 扩容
resize();
}
data[top] = e;
top++;
return true;
}
//出栈操作
public E pop() {
//首先查看一下栈是否为空
if (top == -1) {
throw new RuntimeException("栈为空");
} else {
//将栈顶元素返回后维护一下栈顶指针
return (E) data[top--];
}
}
//查看栈顶元素
public E peek() {
if (top == -1) {
throw new RuntimeException("栈为空");
} else {
// 查看栈顶元素并不移除所以说不需要维护栈顶指针
return (E) data[top];
}
}
// 查看栈是否为空
public boolean isEmpty() {
return maxSize == 0;
}
// 扩容操作
public void resize() {
// 创建一个新数组
Object[] newArray = new Object[data.length * 2];
System.arraycopy(data, 0, newArray, 0, data.length);
data = newArray;
}
}
在顺序栈中,数组的第一个元素最为栈底,最后一个元素最为栈顶。当top=-1的时候,此时栈为空。
每当新增数据入栈push的时候,maxSize加一,同理删除元素出栈pop的时候,maxSize减一。因为是基础数组的实现,所以顺序栈会涉及一个扩容的情况。
- 链式栈
我们再来看看基于链表来实现一个链式栈,代码如下:
public class MyStack<E> {
StackNode<E> top = null; //栈顶
private class StackNode<E>{
E data;
StackNode next;
StackNode(E data) {
this.data=data;
}
}
/**
* 入栈
* 首先将要push的数据的next赋值为栈顶top
* 然后将栈顶指针指向新push进来的节点
* @param data
*/
public void push(E data) {
StackNode<E> newNode = new StackNode<E>(data);
newNode.next = top;
top = newNode;
}
/**
* 出栈
* @return
*/
public E pop() {
if(this.isEmpty()) {
throw new RuntimeException("栈为空");
}
E data = top.data;
top = top.next;
return data;
}
/**
* 查看栈顶元素
* @return
*/
public E peek() {
if(isEmpty()) {
throw new RuntimeException("栈为空");
}
return top.data;
}
// 判断栈是否为空
public boolean isEmpty() {
return top == null;
}
}
在链式栈中,单链表的头部最为栈顶,因为栈的特性是先进后出,所以不需要头节点的。
每当新增数据入栈push的时候,需要让新的结点指向原栈顶,然后再让top指向新增的这个结点。同理删除元素出栈pop的时候,只需要栈顶的 top 指向栈顶元素的 next 指针即可完成删除。
总结
栈作为一个受限制的线性表,只允许对栈顶的数据进行操作,也就是所谓的:先进后出,后进先出。不管是顺序栈还是链式栈,新增或者删除数据时都只能在栈顶进行,故时间复杂度都是O(1),查找数据的时候都需要进行全局遍历,故时间复杂度都是O(n)。顺序栈基于数组实现,初始化时大小便已经固定,后续需要考虑扩容的情况,而链式栈基于链表实现,不需要考虑扩容。