| 排序方法 | 稳定性 | 时间复杂度 | 空间复杂度 | 最好情况 比较次数 | 最坏情况 比较次数 |
|---|---|---|---|---|---|
| 直接插入排序 | 稳定 | O(n2) | O(1) | n-1 | n(n-1)/2 |
| 冒泡排序 | 稳定 | O(n2) | O(1) | n-1 | n(n-1)/2 |
| 简单选择排序 | 不稳定 | O(n2) | O(1) | n(n-1)/2 | n(n-1)/2 |
| 希尔排序 | 不稳定 | O(n1·3) | O(1) | ||
| 快速排序 | 不稳定 | O(nlogn) | O(logn) | ||
| 堆排序 | 不稳定 | O(nlogn) | O(1) | ||
| 归并排序 | 稳定 | O(nlogn) | O(n) | ||
| 基数排序 | 稳定 | O(d(n+rd)) | O(rd) |
1、直接插入排序
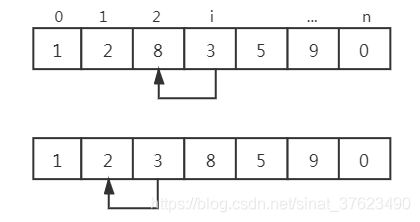
直接插入排序是一种简单的排序方法:n个元素,在对第i(i<=n)个元素排序时,前面的i-1个元素已经有序,此时将待排序的元素依次与前面的第i-1,i-2…2,1个元素进行比较,找到应该插入的位置k,并将k之后的元素依次向后移动一位。
如下图所示,i从位置0开始进行插入排序,到i=3时,前面的3个元素已经按递增排序,则将对应位置元素3与8做比较,由于3较小,将元素插入到第i-1位,并将元素8往后移动一位,将3继续与前面一位元素做比较,3>2,则第i个元素插入结束。
/**
* 直接插入排序
* @param data
* @return
*/
public void insertSort(int[] data){
int i, j, tmp;
for(i=1;i<data.length;i++){
if(data[i]<data[i-1]){
tmp = data[i];//需要交换数据,先保存待插入的数字
for(j=i-1;j>=0&&data[j]>tmp;j--){
data[j+1] = data[j];//比较大的都往后挪一位
}
data[j+1] = tmp;//因为i之前的已经有序,只要有一个小于等于data[i]的数字,这个数字后一位就是插入的位置
}
}
System.out.println(Arrays.toString(data));
}
2、冒泡排序
n个元素进行冒泡排序时,首先将第一个元素和第二个元素进行比较,若为逆序则交换二者位置,此时较大的元素被放到了后面,接着用二者中较大的第二个元素和第三个元素进行比较,依次类推,直到第n-1个元素和第n个元素比较完成后,完成一趟冒泡排序,最大的元素被交换到第n位。
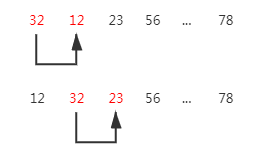
然后对前n-1个元素进行一趟冒泡,结果是第二大的元素交换到第n-1的位置。
完成最多n-1趟冒泡后,所有元素有序排列。某趟冒泡过程中没有进行任何元素交换,则可以结束排序过程。
/**
* 冒泡排序
* @param data
* @return
*/
public void bubbleSort(int[] data){
int i, j;
for(i=0;i<data.length-1;i++){
boolean flag = true;//用于判断本次冒泡是否进行了交换
for(j=0;j<data.length-i-1;j++){//第i次排序时最后i个元素已经有序
if(data[j]>data[j+1]){
swap(data, j, j+1);
flag = false;
}
}
if(flag){
break;//某趟冒泡没有交换则可以结束排序
}
}
System.out.println(Arrays.toString(data));
}
3、简单选择排序
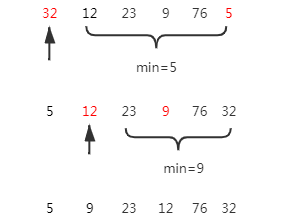
n个元素进行简单选择排序,当排序第i个元素时,通过n-i次对元素间的比较,从n-i+1个元素中选出关键字最小的元素,并和第i个元素交换,当i=n时所有元素有序排列。
/**
* 简单选择排序
* @param data
*/
public void selectSort(int[] data){
int i, j, k;
for(i=0;i<data.length-1;i++){
k = i;//k存放最小元素下标
for(j=i+1;j<data.length;j++){
if(data[j]<data[k]){
k = j;//记录当前最小元素的下标
}
}
if(k != i){//存在比data[i]更小元素,交换data[i]与data[k]
swap(data, i, k);
}
}
System.out.println(Arrays.toString(data));
}
4、希尔排序
希尔排序是对直接插入排序方法的改进。
其基本思想是:对待排序的n个元素,首先取d1(d1<n)作为分组间距,将所有距离为d1倍数的元素放在同一组中,由此将所有待排列元素分为d1组,在每个组内做直接插入排序;接着取d2(d2<d1)作为分组间距的带d2个组,组内进行直接插入排序…重复上述操作直到di=1,此时得到所有待排序元素分为一组切基本有序,进行直接插入排序可以得到最终有序排列的数组。

/**
* 希尔排序
* @param data
*/
public void shellSort(int[] data){
int i, j, k, s, tmp;
k = data.length;
int[] dist = new int[k/2];
i = 0;
do{
k = k / 2;
dist[i++] = k;
}while(k > 1);//得到每次分组的间距,直到1为止
for(i=0;(s = dist[i])>0;i++){//取分组间距
System.out.println("分组间距:" + s + ",此次排序得到:");
for(k=s;k<data.length;k++){//对每个分组内元素做直接插入排序
if(data[k] < data[k-s]){
tmp = data[k];
for(j=k-s;j>=0&&data[j]>tmp;j-=s){
data[j+s] = data[j];
}
data[j+s] = tmp;
}
}
System.out.println(Arrays.toString(data));
}
}
5、快速排序
快速排序的基本思想是:通过一趟排序将待排的元素划分为独立的两部分,成为前半区和后半区。前半区中的元素都不大于后半区中的元素。然后再分别对这两部分进行快速排序,进而使整个序列有序。
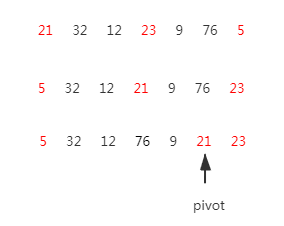
快速排序中一次划分的具体方法是:设待排序元素中的一个元素为枢轴元素pivot,另外设两个指针 i 和 j 分别指向序列的首尾位置。假设本次枢轴元素取i最初指向元素,则首先从j所指位置起向前搜索,找到第一个小于pivot的元素时,将该元素移到i所指的位置;然后从i所在位置开始向后搜索,找到第一个大于pivot的元素时将其移到j所指位置。重复该过程直到i等于j,将pivot复制到i和j指向位置。同理,若枢轴元素取j最初指向元素,则首先从i所指位置向后搜索。
如下图所示,对数组进行一次划分得到前半区[5,9,12,21]和后半区[23,76,32],再分别对两个分区进行快速排序,即可得到有序序列[5,9,12,21,23,32,76]。
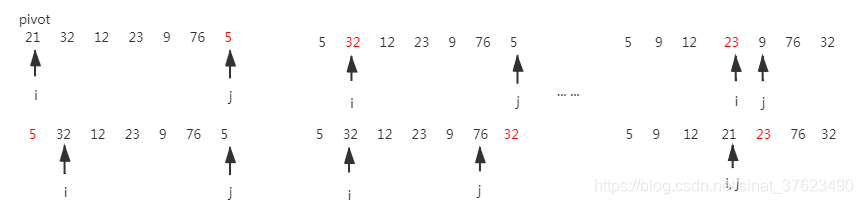
快速排序被认为是在复杂度为O(nlogn)的排序方法中最好的一种,但是若初始序列元素有序或基本有序时,每次划分结果都会得到一个长度为0的分区,此时快速排序的性能退化为O(n2)。为了避免性能退化,一般会在选择枢轴元素时采用三数取中的方法。
三数取中:即在待排序数组中对首、中、尾三个元素进行大小比较,选择中间值的元素作为枢轴元素。
/**
* 快速排序
* @param data
*/
public void quickSort(int[] data, int low, int high){
if(low < high){
int loc = partition(data, low, high);//进行一次分区
quickSort(data, low, loc - 1);//对前半区快速排序
quickSort(data, loc + 1, high);//对后半区快速排序
}
}
/**
* 一次划分后,得到数组以枢轴元素data[i]为界,前半区元素都不大于data[i],后半区元素都不小于data[i]
* @param data
* @param low
* @param high
* @return
*/
public int partition(int[] data, int low, int high){
getPivot(data, low, high);
int pivot = data[high-1];//枢轴元素
int i = low;
int j = high - 1;
while(i < j){
while(i < j && data[++i] <= pivot){}
data[j] = data[i];//data[i]大于pivot,移到后半区,此时原data[j]的值已保存在pivot或data[i]中
while(i < j && data[--j] >= pivot){}
data[i] = data[j];//data[j]小于pivot,移到前半区,此时原data[i]的值已保存在data[j]中
}
data[i] = pivot;
return i;
}
/**
* 取首、中、尾三者中间大小元素,避免快速排序性能退化
* @param data
* @param low
* @param high
*/
public void getPivot(int[] data, int left, int right){
int mid = (left + right) / 2;
//对三个元素按递增排序
if (data[left] > data[mid]) {
swap(data, left, mid);
}
if (data[left] > data[right]) {
swap(data, left, right);
}
if (data[right] < data[mid]) {
swap(data, right, mid);
}
//将枢轴元素放置在待排序数组后
swap(data, right-1, mid);
}
/**
* 快速排序非递归
* @param data
*/
public void quickSortNotRecur(int[] data, int low, int high){
//使用栈来实现递归的压栈出栈操作
Stack<Object> s = new Stack<Object>();
s.push(low);
s.push(high);
if(!s.empty()){
high = (Integer) s.pop();
low = (Integer) s.pop();
int loc = partition(data, low, high);//进行一次分区
s.push(loc+1);//后半区先进后出
s.push(high);
s.push(low);//前半区后进先出
s.push(loc-1);
}
}
6、堆排序
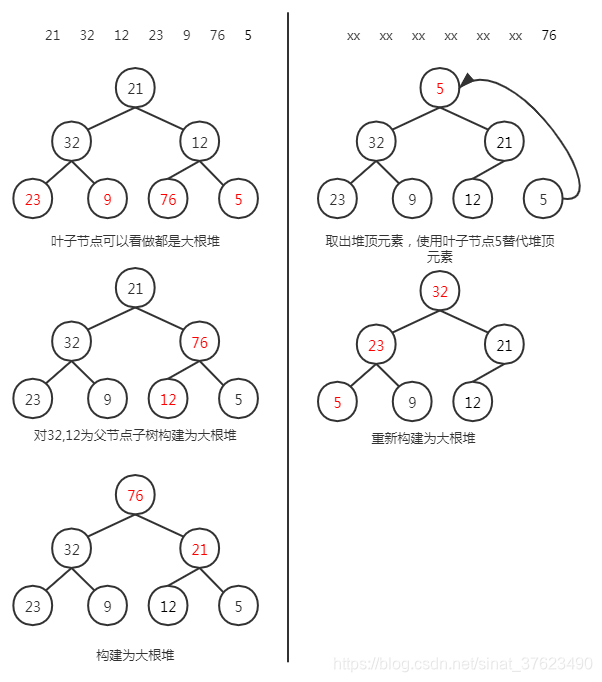
对待排列的n个元素组成的序列,将其看成一个完全二叉树,如果该二叉树中的任一非叶子节点的值均不小于(不大于)其左右子树节点,则该二叉树称为大根堆(小根堆),树的根节点(堆顶元素)是序列中最大(最小)的元素。
堆排序的基本思想是:对待非递减排列的序列首先建立一个初始堆,此时输出堆顶元素,即最大值元素,然后取最后一个叶子节点替代堆顶元素,并将剩下的元素重新构建为大根堆,再输出新堆的堆顶元素作为次大值元素…以此类推,直到所有的元素有序排列。
/**
* 堆排序
* @param data
*/
public void heapSort(int[] data){
int i, n, tmp;
n = data.length;
for(i=n/2-1;i>=0;i--){//从n位置子节点所在子树开始向上调整整个数组为大根堆(构建初始堆)
heapAdjust(data, i, n-1);
}
for(i=n-1;i>0;i--){//从初始堆取堆顶(最大元素),对剩余元素重新构建大根堆
tmp = data[0];//取堆顶
data[0] = data[i];//将最末尾子节点交换到堆顶
data[i] = tmp;//当前最大值放到数组末尾
heapAdjust(data, 0, i-1);//剩余i-1个元素构建大根堆
}
System.out.println(Arrays.toString(data));
}
/**
* 将待排序元素调整为大根堆
* @param data
* @param s
* @param m
*/
public void heapAdjust(int[] data, int s, int m){
int i, tmp;
tmp = data[s];//备份当前父节点关键字
for(i=2*s+1;i<=m;i=2*i+1){
if(i<m && data[i]<data[i+1]){//找到子节点中关键字最大者
i++;
}
if(tmp>=data[i]) break; //所有子节点都不大于父节点,本次无需调整
data[s] = data[i]; //存在比父节点大的子节点,插入s位置
s = i; //以i作为父节点的子树可能因为本次调整不再是大根堆,因此需要进行调整
}
data[s] = tmp;//将备份关键字插入最后做了交换的节点位置
}
7、归并排序
归并排序的一种实现方法是把一个有n个记录的无序文件看成是由n个长度为1的有序子文件组成的文件,对子文件两两归并,得到n/2个长度为2或1的有序文件,再两两归并,重复得到一个包含n个记录的有序文件。
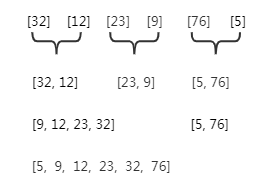
假设一次归并的两个文件为数组arr1和数组arr2,则需要一个大小为arr1和arr2长度之和的辅助空间arrTmp来进行归并,此时三个指针分别指向arr1,arr2和arrTmp初始位置,每次对比arr1和arr2指针指向元素,将其中较小值插入到arrTmp指针所指位置。当arr1,arr2中任一数组末尾元素插入到了arrTmp中,则将另一个数组剩余元素直接全部插入arrTmp中即可。如下图所示:

/**
* 归并排序
* @param data
* @param s
* @param t
*/
public void mergeSort(int[] data, int left, int right){
if(left < right){
int mid = (left + right) >> 1;
mergeSort(data, left, mid);//前半区归并得到有序子序列data[left..mid]
mergeSort(data, mid + 1, right);//后半区归并得到有序子序列data[mid..right]
merge(data, left, mid, right);//data[left..mid]和data[mid..right]归并得到有序的data[s..t]
}
}
/**
* 对两个序列data[s..m]和data[m+1..n]进行归并
* @param data
* @param s
* @param m
* @param n
*/
public void merge(int[] data, int s, int m, int n){
int i = s, j = m + 1, k = 0;//i指向data[m+1..n]初始位置,j指向data[s..m]初始位置,k指向tmp[]初始位置
int st = s;
int[] tmp = new int[data.length];
while(i<=m&&j<=n){//归并data[s..m]和data[m+1..n]存入临时数组tmp[]
if(data[i]<=data[j]){
tmp[k++] = data[i++];
}else{
tmp[k++] = data[j++];
}
}
for(;i<=m;i++){//将剩余data[s..m]元素复制到tmp[]
tmp[k++] = data[i];
}
for(;j<=n;j++){//将剩余data[m+1..n]元素复制到tmp[]
tmp[k++] = data[j];
}
for(i=0;i<k;i++){//将临时数组元素复制回原数组
data[st++] = tmp[i];
}
//用于输出信息
if(s == 0 && n == data.length-1 >> 1){
System.out.println("前半区归并完成:" + Arrays.toString(data));
}
if(s == data.length >> 1 && n == data.length - 1){
System.out.println("后半区归并完成:" + Arrays.toString(data));
}
}
8、基数排序
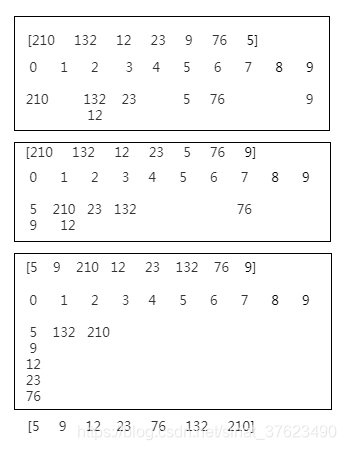
基数排序是一种通过比较元素各个位数大小来进行排序的方法:基数r是按照元素数值的进制来确定的,比如十进制r=10,八进制则r=8。d原来表示元素的位数,d取所有待排序元素的位数最大值,比如125则d=3。
进行基数排序时,设立r个队列,队列编号分别从0到r-1。首先按照最低有效位大小将元素分别排进队列中,然后按照队列中的顺序将元素重新排列。接着按照次低有效位将重新排列好的元素再次排进队列中…如此重复直到最高有效位完成排列,此时从队列取出的元素有序排列。
/**
* 基数排序
* @param data
*/
public void radixSort(int[] data){
//确定最大位数
int max = data[0];
for(int x: data){
if(x > max){
max = x;
}
}
int length = (max+"").length();
for(int i=0,n=1;i<length;i++,n*=10){
int[][] tmp = new int[10][data.length];
int[] queLength = new int[10];//保存每个队列入队元素个数
//将数组元素一一入队
for(int x: data){
int index = x / n % 10;//确定元素应入队列
tmp[index][queLength[index]++] = x;
}
//将队列中元素重新排列为数组
int dataIdx = 0;
for(int j=0;j<10;j++){
for(int q=0;q<queLength[j];q++){
data[dataIdx++] = tmp[j][q];
}
}
}
System.out.println(Arrays.toString(data));
}
运行实例
import java.util.Arrays;
import java.util.Stack;
public class Sort {
final int[] data = {76,34,18,12,45,5,5,9};
public static void main(String args[]){
Sort sort1 = new Sort();
System.out.print("**直接插入排序\n原数组:" + Arrays.toString(sort1.data) + "\n排序后:");
sort1.insertSort(sort1.data);
Sort sort2 = new Sort();
System.out.print("\n**冒泡排序\n原数组:" + Arrays.toString(sort2.data) + "\n排序后:");
sort2.bubbleSort(sort2.data);
Sort sort3 = new Sort();
System.out.print("\n**简单选择排序\n原数组:" + Arrays.toString(sort3.data) + "\n排序后:");
sort3.selectSort(sort3.data);
Sort sort4 = new Sort();
System.out.print("\n**希尔排序\n原数组:" + Arrays.toString(sort4.data) + "\n");
sort4.shellSort(sort4.data);
Sort sort5 = new Sort();
System.out.print("\n**快速排序\n原数组:" + Arrays.toString(sort5.data) + "\n排序后:");
sort4.quickSort(sort5.data, 0, sort5.data.length - 1);
System.out.println(Arrays.toString(sort5.data));
Sort sort51 = new Sort();
System.out.print("\n**快速排序(非递归)\n原数组:" + Arrays.toString(sort51.data) + "\n排序后:");
sort4.quickSort(sort51.data, 0, sort51.data.length - 1);
System.out.println(Arrays.toString(sort51.data));
Sort sort6 = new Sort();
System.out.print("\n**堆排序\n原数组:" + Arrays.toString(sort6.data) + "\n排序后:");
sort4.heapSort(sort6.data);
Sort sort7 = new Sort();
System.out.println("\n**归并排序\n原数组:" + Arrays.toString(sort7.data));
sort4.mergeSort(sort7.data, 0, sort7.data.length - 1);
System.out.println("排序后:" + Arrays.toString(sort7.data));
Sort sort8 = new Sort();
System.out.print("\n**基数排序\n原数组:" + Arrays.toString(sort8.data) + "\n排序后:");
sort4.radixSort(sort8.data);
}
public void swap(int[] data, int i, int j){
int tmp = data[i];
data[i] = data[j];
data[j] = tmp;
}
}
输出结果:
**直接插入排序
原数组:[76, 34, 18, 12, 45, 5, 5, 9]
排序后:[5, 5, 9, 12, 18, 34, 45, 76]
**冒泡排序
原数组:[76, 34, 18, 12, 45, 5, 5, 9]
排序后:[5, 5, 9, 12, 18, 34, 45, 76]
**简单选择排序
原数组:[76, 34, 18, 12, 45, 5, 5, 9]
排序后:[5, 5, 9, 12, 18, 34, 45, 76]
**希尔排序
原数组:[76, 34, 18, 12, 45, 5, 5, 9]
分组间距:4,此次排序得到:
[45, 5, 5, 9, 76, 34, 18, 12]
分组间距:2,此次排序得到:
[5, 5, 18, 9, 45, 12, 76, 34]
分组间距:1,此次排序得到:
[5, 5, 9, 12, 18, 34, 45, 76]
**快速排序
原数组:[76, 34, 18, 12, 45, 5, 5, 9]
排序后:[5, 5, 9, 12, 18, 34, 45, 76]
**快速排序(非递归)
原数组:[76, 34, 18, 12, 45, 5, 5, 9]
排序后:[5, 5, 9, 12, 18, 34, 45, 76]
**堆排序
原数组:[76, 34, 18, 12, 45, 5, 5, 9]
排序后:[5, 5, 9, 12, 18, 34, 45, 76]
**归并排序
原数组:[76, 34, 18, 12, 45, 5, 5, 9]
前半区归并完成:[12, 18, 34, 76, 45, 5, 5, 9]
后半区归并完成:[12, 18, 34, 76, 5, 5, 9, 45]
排序后:[5, 5, 9, 12, 18, 34, 45, 76]
**基数排序
原数组:[76, 34, 18, 12, 45, 5, 5, 9]
排序后:[5, 5, 9, 12, 18, 34, 45, 76]