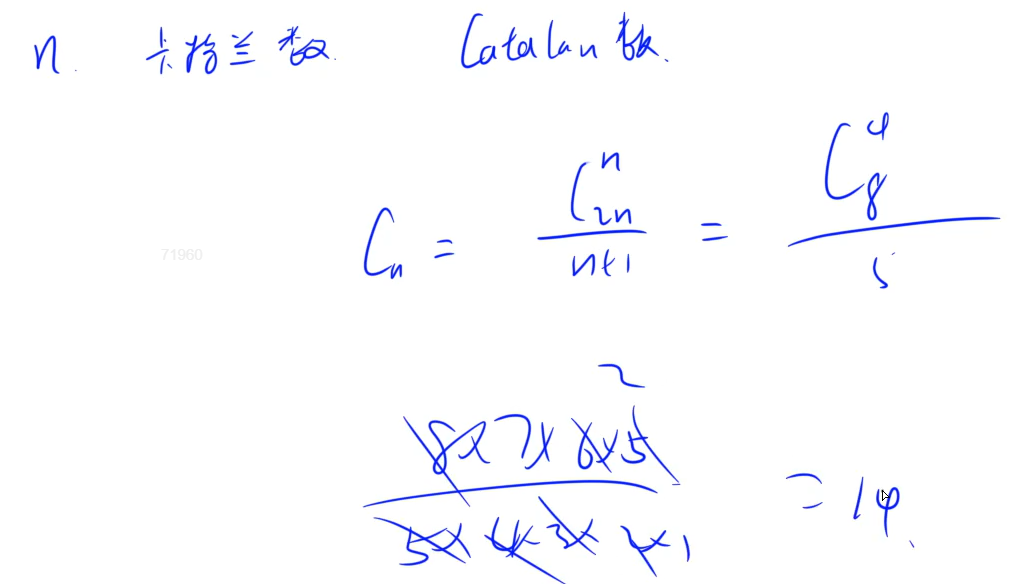第四讲 树的基本概念、二叉树、树和森林
文章目录
1. 树的基本概念
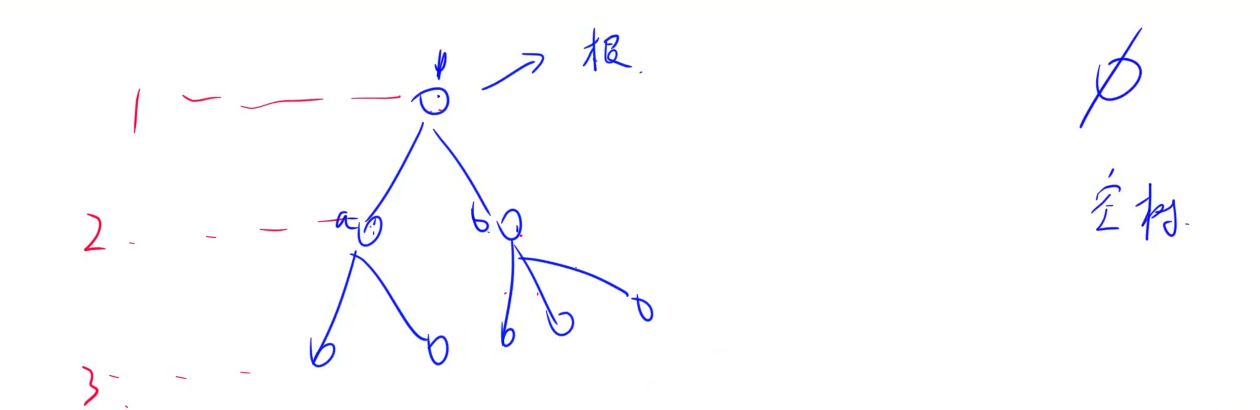
(1) 树是由根节点和若干颗子树构成的。树是由一个集合以及在该集合上定义的一种关系构成的。集合中的元素称为树的节点,所定义的关系称为父子关系。父子关系在树的节点之间建立了一个层次结构。在这种层次结构中有一个节点具有特殊的地位,这个节点称为该树的根节点,或称为树根。
(2) 空集合也是树,称为空树。空树中没有节点;
(3) 孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点;
(4) 节点的度:一个节点含有的子节点的个数称为该节点的度;
(5) 叶节点或终端节点:度为0的节点称为叶节点;
(6) 非终端节点或分支节点:度不为0的节点;
(7) 双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点;
(8) 兄弟节点:具有相同父节点的节点互称为兄弟节点;
(9) 树的度:一棵树中,最大的节点的度称为树的度;
(10) 节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
(11) 树的高度或深度:树中节点的最大层次;
(12) 节点的祖先:从根到该节点所经分支上的所有节点;
(13) 子孙:以某节点为根的子树中任一节点都称为该节点的子孙;
(14) 森林:由棵互不相交的树的集合称为森林。
理解理解理解
2. 二叉树
(1) 二叉树的定义及其主要特征
a. 二叉树的基本形态:空二叉树、单节点二叉树、左子树、右子树
? b. 性质:
? [1] 在非空二叉树中,第i层上至多有2^(i-1) 个结点。
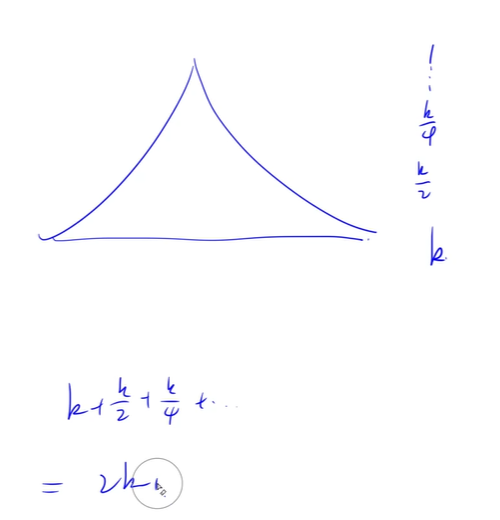
? [2] 深度为k的二叉树至多有2^k - 1个结点
? [3] 对任何一颗二叉树,若其叶子结点数为n0,度为2的结点数为n2,则n0 = n2 + 1。
? [4] n个结点的完全二叉树深度为:log2(n)向下取整 + 1
? [5] 二叉树的堆式存储: 节点p (编号p)的左儿子:2p,右儿子:2p+1
?
? // r = [p/2]下取整
? c. 两种特殊的二叉树
? [1] 满二叉树:一颗深度为k且有2^k-1个结点的二叉树
? [2] 如果深度为k,有n个结点的二叉树,当且仅当其每个结点都与深度为k的满二叉树中编号从1到n的结点一一对应,该二叉树称为完全二叉树
(2) 二叉树的顺序存储结构和链式存储结构
? 链式存储结构
? /**c++:
? * Definition for a binary tree node.
? * struct TreeNode {
? * int val;
? * TreeNode *left;
? * TreeNode *right;
? * TreeNode(int x) : val(x), left(NULL), right(NULL) {}
? * };
? */
?
(3) 二叉树的遍历
a. 前序遍历 dfs
b. 中序遍历
c. 后序遍历
d. 根据前序 + 中序重建二叉树 (AcWing 18. 重建二叉树)
层次遍历不考 bfs
?
(4) 线索二叉树的基本概念和构造
? 对二叉树节点的指针域做如下规定:
? a. 若节点有左孩子,则Lchild指向左孩子,否则指向直接前驱;右孩子同理;
? b. 增加两个标志域,Ltag表示指向的是子节点还是前驱;Rtag同理
? c. 指向前驱和后继的指针叫做线索。按照某种次序遍历,加上线索的二叉树称之为线索二叉树


n = n0 + n1 + n2
n-1边
n-1 = 0n0 + 1 * n1 + 2n 2
n0 + n1 + n2 - 1 == 0n0 + 1 * n1 + 2n 2
n0 - 1 == n 2
n0 = n2 + 1
1
前序+中序 —>> 构造二叉树
3. 树、森林
(1) 树的存储结构
a. 只存父节点
b. 邻接表存储所有子节点
c. 左儿子右兄弟
(2) 森林F与二叉树T的转换
a. 原树中叶子节点数 = 转换后的树中有右儿子的节点数 + 1
b. F的前序遍历就是T的前序遍历
c. F的后序遍历就是T的中序遍历
(3) 树和森林的遍历
a. 前序遍历
b. 后序遍历
4. 考题:2011-4、2011-5、2011-6、2012-3、2013-5、2014-4、2014-5、2014-41、2015-2、2016-5、2016-42、2017-4、2017-5、2018-4、2019-2、2020-3、2020-4
2011-4

分析:求叶节点 n0
768 = n0+n1+n2
n0 = n2+1 ;
2*n2 +1 + n1 = 768
768 为偶数 n1 =1 ,多一个
2*n2 = 766
n2 = 383
n0 = n2+ 1 = 384 ;
2011-5

前序和后序遍历 不能唯一确定 树
选择题 可以用 前序和 中序来判断
2011-6
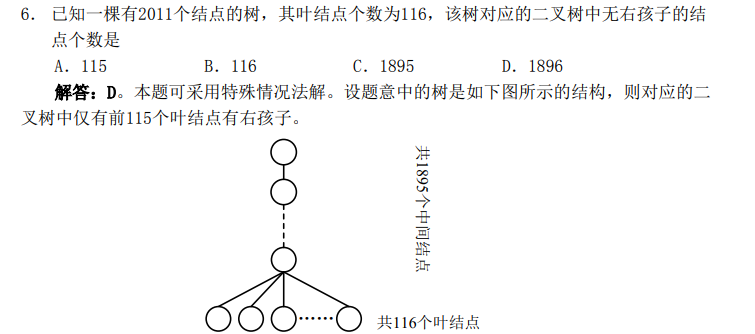
用结论 : 原树中叶子节点数 = 转换后的树中有右儿子的节点数 + 1
树中有右儿子的节点数 116 == 115 + 1
2011 - 115 = 1896
2012-3

A
2013-5

A
后序线索二叉树:看后序遍历
线索二叉树:若节点有左孩子,则Lchild指向左孩子,否则指向直接前驱;右孩子同理
X 有 左兄弟 ,为叶节点 没有孩子
指向直接前驱 x 的父节点 yxp
2014-4
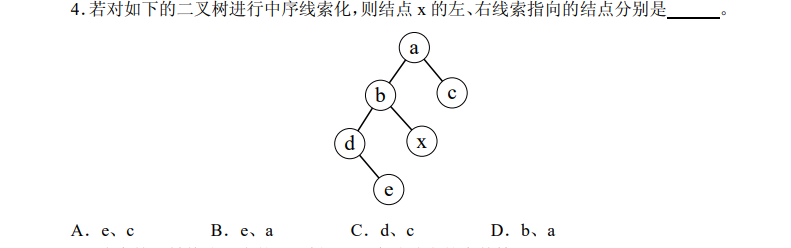
中序线索化:看中序遍历
debxac
选D
2014-5

森林>>二叉树 左儿子 右兄弟
兄弟 == 儿子? yes
叶节点: 没有孩子
所以为没有左孩子的
选C
2014-41

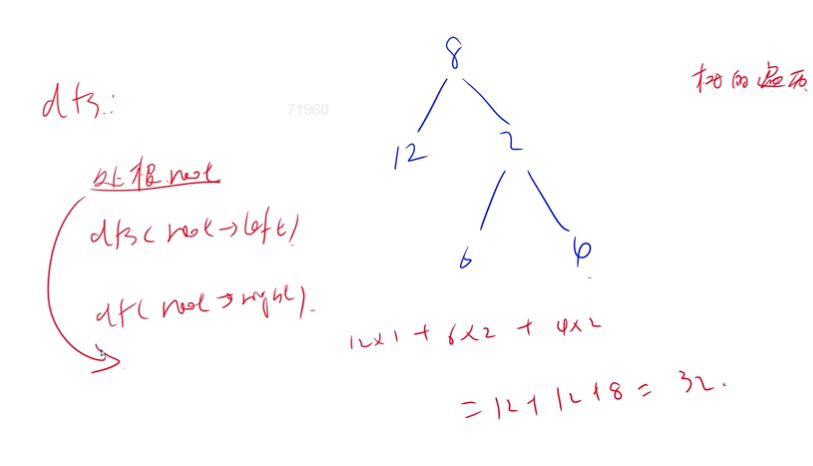
带权路径 : 权值* 到根节点的距离
树的遍历 , 推荐dfs实现 即递归
C++:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
int dfs(TreeNode* root,int depth){ // depth 为深度
if(!root) return 0; //如果是空
// 如果是叶节点: 没有左右孩子
if(!root->left&&!root->right) return root->val*depth;
else {
// 左右遍历 返回左右子树权值
return dfs(root->left,depth+1)+ dfs(root->right,depth+1);
}
}
int pathSum(TreeNode* root) {
return dfs(root , 0);
}
};
c:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
int dfs(struct TreeNode* root,int depth){
if(!root ) return 0;
if(!root->left&&!root->right) return root->val*depth;
else{
return dfs(root->left,depth+1)+ dfs(root->right,depth+1);
}
}
int pathSum(struct TreeNode* root) {
return dfs(root , 0);
}
2015-2

包含4个点的二叉树数量
N 卡特兰数
2016-5

25个结点 24条边
每删一条边多一颗树
删了24 - 15 = 9 棵
9+1 = 10 棵
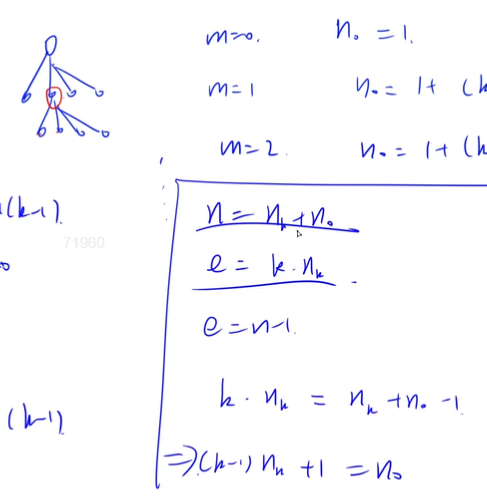
2016-42

归纳法:
n = nk+ n0
e = k* nk
e = n - 1
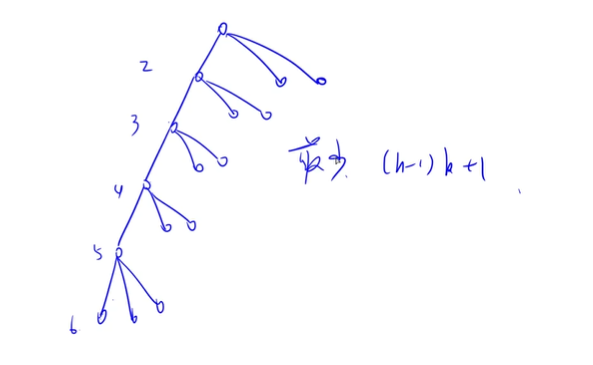
最多为满二叉树
2017-4

B
2017-5
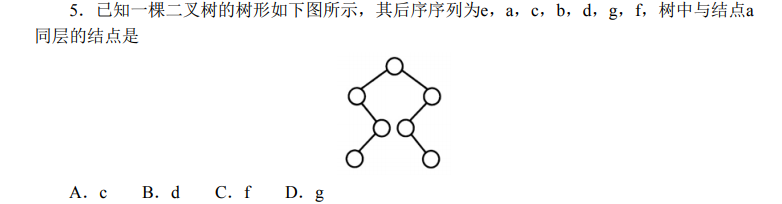
B
2018-4

满二叉树
2019-2

B
2020-3

要存下任意一棵树,最坏情况
1+2 +4 +8 +16 = 31
2^5-1 = 31
2020-4
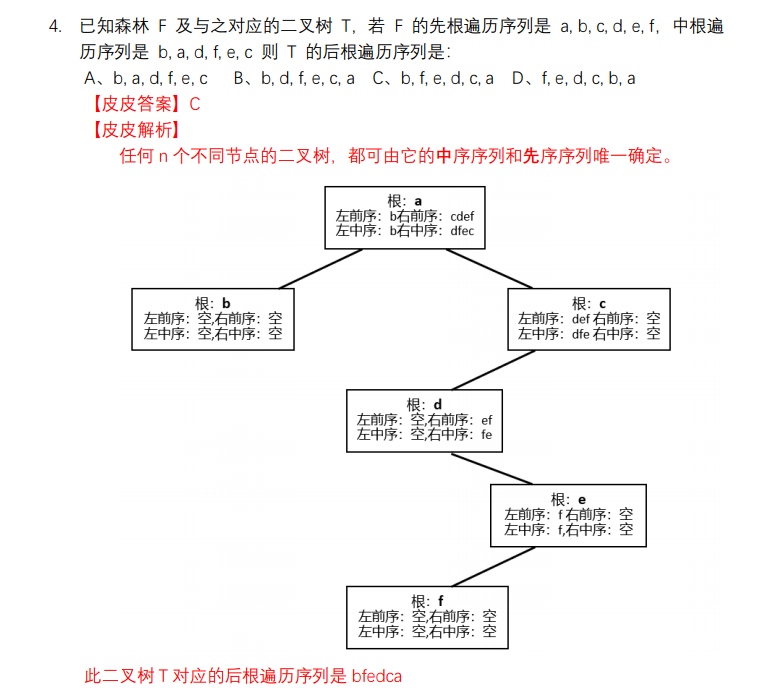
5. 押题:AcWing 19
线索二叉树。
算法
(模拟) O(h)O(h)
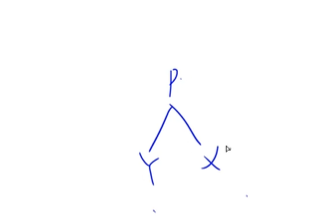
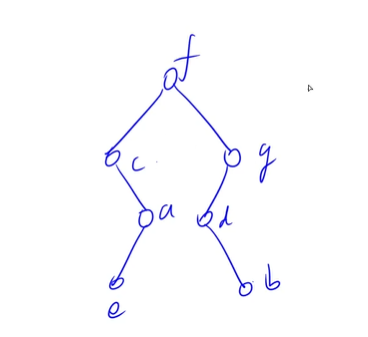
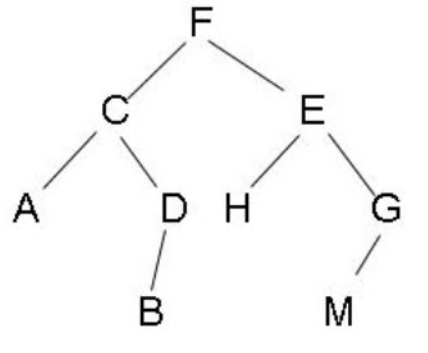
这道题目就是让我们求二叉树中给定节点的后继。分情况讨论即可,如下图所示:
1.如果当前节点有右儿子,则右子树中最左侧的节点就是当前节点的后继。比如F的后继是H;
2.如果当前节点没有右儿子,则需要沿着father域一直向上找,找到第一个是其father左儿子的节点,该节点的father就是当前节点的后继。比如当前节点是D,则第一个满足是其father左儿子的节点是F,则C的father就是D的后继,即F是D的后继。
c++:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode *father;
* TreeNode(int x) : val(x), left(NULL), right(NULL), father(NULL) {}
* };
*/
class Solution {
public:
TreeNode* inorderSuccessor(TreeNode* p) {
// 1.如果当前节点有右儿子,则右子树中最左侧的节点就是当前节点的后继
if(p->right) {
p= p->right ;
while(p->left ) p=p->left;
return p;
}
// 2. 如果当前节点没有右儿子,则需要沿着father域一直向上找,找到第一个是其father左儿子的节点,该节点的father就是当前节点的后继。
while(p->father&& p == p->father->right) p = p->father;
return p->father;
}
};