前言
最长递增子序列是笔试常考题,但是每次做,每次都忘记了动态转移方程,在此记录一下,同时加深一下印象。
一、最长递增子序列
最长递增子序列简称LIS,是一道非常经典的算法问题,力扣是300题,再刷华为牛客网的笔试题时,起码遇到过三次,在这里仅介绍动态规划解法,至于二分查找,由于我也没看,就不做介绍了,动态规划解法的时间复杂度时O(n^2),二分查找的时间复杂度是O(nlogn),先以力扣300题进行介绍,题目入下图所示

1.首先要明确dp的含义:dp[i]表示以nums[i]结尾的最长递增子序列**(该序列一定要包含nums[i])**的长度,这个定义一定要理解清楚,如果忘记了,再回头看看。接下来以题目中的例子解释一下dp[i]:
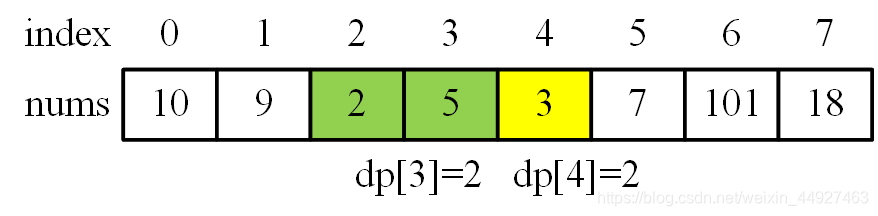
可以看出dp[3]也就是以nums[3]结尾的最长递增子序列为2,也就是2和5这个子序列,再强调一遍该子序列一定包含nums[3]这个数字,dp[4]也就是以以nums4]结尾的最长递增子序列为2,但是该最长子序列不是2和5,而是2和3,也是上述的原因,dp[4]必须包括nums[4],也就是如果nums[4]=1,那么dp[4]为1。
2.接下来是base case也就是dp[i]的初始值:可以看出dp[i]的初始值为1,也就是该子序列为自己。
vector<int> dp(nums.size(), 1);
而最终结果是遍历dp,找到dp中最大值,因为dp[i]是以nums[i]为结尾的最长子序列,所以dp[dp.size()-1]不一定是最大值。
int result = 0;
for(int i = 0; i < dp.size(); i++){
result = max(result, dp[i]);
}
3.最后就是找动态转移方程。
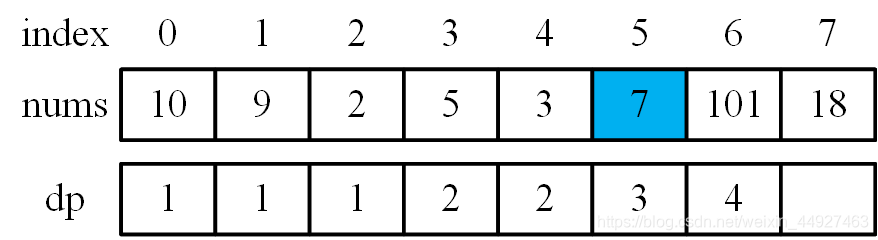
如上图所示,已经求出dp[0]到dp[6],该如何求dp[7]呢?根据dp定义,dp[7]就是以nums[7]为结尾的最长递增子序列,nums[7] = 18,所以我们只要找到前面那些结尾比18小的子序列,将18加到后面即可,所以长度就是+1
//第一层遍历是为了求dp[i]
for(int i = 1; i < nums.size(); i++){
//第二层遍历是找前面那些结尾比nums[i]小的子序列
for(int j = 0; j < i; j++){
if(nums[j] < nums[i]) {
dp[i] = max(dp[i], dp[j] + 1);
}
}
}
int lengthOfLIS(vector<int>& nums) {
if(nums.size() == 1) return 1;
vector<int> dp(nums.size(), 1);
int result = 0;
//第一层遍历是为了求dp[i]
for(int i = 1; i < nums.size(); i++){
//第二层遍历是找前面那些结尾比nums[i]小的子序列
for(int j = 0; j < i; j++){
if(nums[j] < nums[i]) {
dp[i] = max(dp[i], dp[j] + 1);
}
}
}
//找dp中的最大值
for(int i = 0; i < dp.size(); i++){
result = max(result, dp[i]);
}
return result;
}
二、笔试题目—合唱队

代码
#include <iostream>
#include <vector>
using namespace std;
int myfun(vector<int>& vec){
int n = vec.size();
//注意dp[i]表示以vec[i]为结尾的最大子序列大小
vector<int> dp1(n, 1);
vector<int> dp2(n, 1);
for(int i = 0; i < n; i++){
for(int j = 0; j < i; j++){
if(vec[j] < vec[i]){
dp1[i] = max(dp1[i], dp1[j] + 1);
}
}
}
for(int i = n - 1; i >= 0; i--){
for(int j = n - 1; j > i; j--){
if(vec[j] < vec[i]){
dp2[i] = max(dp2[i], dp2[j] + 1);
}
}
}
int ans = 0;
for(int i = 0; i < n; i++){
ans = max(ans, dp1[i] + dp2[i] - 1);
}
return n - ans;
}
int main(void){
vector<int> vec;
int n;
while(cin>>n){
int h;
for(int i = 0; i < n; i++){
cin>>h;
vec.push_back(h);
}
cout<<myfun(vec)<<endl;
vec.clear();
}
return 0;
}