2021/07/26

逻辑回归

逻辑回归是一个分类算法，仅适用于二分类并且还能得出概率。而且是以线性回归的式子作为输入的分类算法。
我打个比方说网站上的广告，用户可以选择点击广告和不点击广告。这是一个二分类问题，更厉害的是逻辑回归可以预测出，用户会有多少几率去点击（或者理解为有百分之多少的用户会点击广告）。这样网站也就能通过逻辑回归提前预测出上广告会有多少收益。
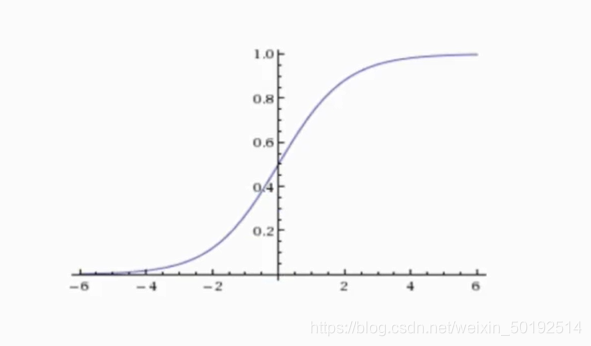
在这里插入图片描述

上图就是Sigmoid函数。通俗来讲 0.5是一个阈值，Sigmoid函数结果只能是0到1之间（也对应了概率中的几率大小），对于结果小于0.5的数逻辑回归就按0处理；对于结果大于0.5的数，逻辑回归就按1处理。

逻辑回归的损失函数

逻辑回归的损失函数和线性回归的原理相同，但是由于是分类问题，所以损失函数稍微不一样。用的是对数似然损失函数
在这里插入图片描述
h（x）指的是概率，log（h（x））有点前面提过信息熵的感觉
如下图，如果y= 1，目标值为1.的意思是：如果预测的结果是1类概率h（x）为0.7，那么损失值就是图线靠右的那个点，损失值也相对较小

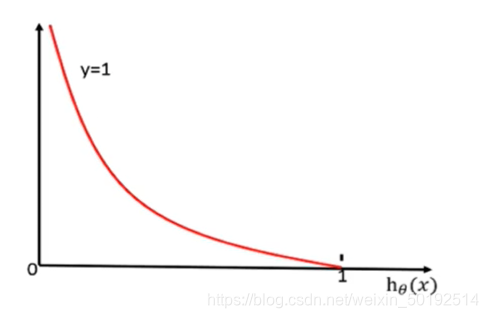
如果y=0，就和y=1的图相反如下图。目标值为0. 那么预测结果为0类概率h(x)同样为0.7，那么损失值的点也在靠右边，损失值会相对的变大
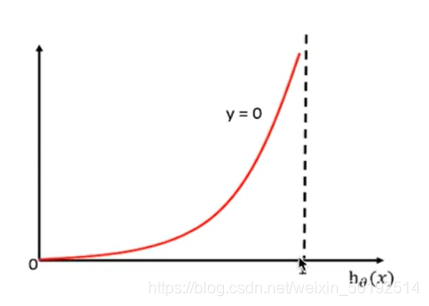
在这里插入图片描述
上面说的对数似然损失函数只是一个样本得出的结果，如果一个模型的的损失函数就得看下面这个公式：

举个栗子吧：
有[样本1，样本2，样本3，样本4]实际结果是[1,0,0,1]
经过逻辑回归属于1的概率是[0.65, 0.12,0.55,0.78]
使用完整损失函数四个损失值相加为1log(0.65)+0log(0.12)+0log(0.55)+1log(0.78)
这块有点和信息熵相似带有log（）。数字越大，一个是误差就越大，一个信息熵越大。

损失函数

目前学到了两种损失函数

一个是均方误差（直接找到误差最小的一个点）
一个是对数似然损失函数，有多个局部最小值，用梯度下降优化。对于有多个局部最小值只能通过1.多次初始化，比较最小值。2调整梯度下降的学习率，比较找到最小值。

逻辑回归API

sklearn.linear_model.LogisticRegression(penalty='l2',C=1.0)
penalty='l2’正则化
C 也是一种正则化力度，和岭回归一样能很好的解决过拟合问题
只能解决二分类问题，比如：

广告点击率
是否为垃圾邮件
是否患病
是否为金融诈骗
是否为虚假账号

案例：癌症肿瘤预测

数据地址是 https://archive.ics.uci.edu/ml/machine-learning-databases/breast-cancer-wisconsin/breast-cancer-wisconsin.data

在这里插入图片描述
数据的内容如上图。在逻辑回归中，哪个占比少就把哪个当做目标值，比如这个案例中恶性少，逻辑回归就会把恶性为正例，反之良性为反例。
案例主要流程和思路

网上获取数据
对数据缺失值做处理，进行标准化
逻辑回归流程

from sklearn.linear_model import LinearRegression, SGDRegressor,  Ridge, LogisticRegression
from sklearn.metrics import  classification_report
import pandas as pd
import numpy as np


def logistic():
    """
    逻辑回归做二分类进行癌症预测（根据细胞的属性特征）
    :return: NOne
    """
    # 构造列标签名字
    column = ['Sample code number','Clump Thickness', 'Uniformity of Cell Size','Uniformity of Cell Shape','Marginal Adhesion', 'Single Epithelial Cell Size','Bare Nuclei','Bland Chromatin','Normal Nucleoli','Mitoses','Class']

    # 读取数据
    data = pd.read_csv("https://archive.ics.uci.edu/ml/machine-learning-databases/breast-cancer-wisconsin/breast-cancer-wisconsin.data", names=column)

    print(data)

    # 缺失值进行处理
    data = data.replace(to_replace='?', value=np.nan)

    data = data.dropna()

    # 进行数据的分割
    x_train, x_test, y_train, y_test = train_test_split(data[column[1:10]], data[column[10]], test_size=0.25)

    # 进行标准化处理
    std = StandardScaler()

    x_train = std.fit_transform(x_train)
    x_test = std.transform(x_test)

    # 逻辑回归预测
    lg = LogisticRegression(C=1.0)

    lg.fit(x_train, y_train)

    print(lg.coef_)

    y_predict = lg.predict(x_test)

    print("准确率：", lg.score(x_test, y_test))

    print("召回率：", classification_report(y_test, y_predict, labels=[2, 4], target_names=["良性", "恶性"]))

    return None


if __name__ == "__main__":
    logistic()