一:提升树模型
提升树是以分类树或回归树为基分类器的提升方法,提升树被认为是统计学习中性能最好的方法之一
提升方法实际采用前向分步算法和加法模型(即基函数的限行组合),以决策树为基函数的提升方法称为提升树,对分类问题的决策树是二叉分类树,对回归问题的决策树是二叉回归树。提升树的模型可以表示为决策树的加法模型:

二:提升树算法
提升树算法采用前向分步算法,首先确定初始提升树Fo(x) = 0,第m步的模型为:

通过经验风险最小化,那么决策树的参数θm可表示为:
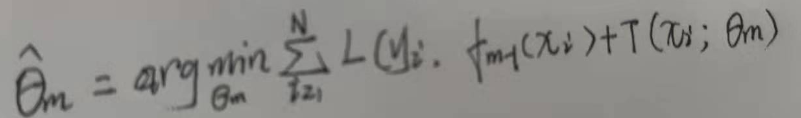
二:不同的提升树学习算法
针对不同问题的提升树学习算法,其主要区别在于使用的损失函数不同。主要有
1,使用平方误差损失函数的回归问题
2,使用指数损失函数的分类问题
3,使用一般损失函数的一般决策问题
(一)使用指数损失函数的分类问题提升树:对于二分类问题,只需要将Adaboost算法中的基分类器限定为二分类树即可。可以说这时候的提升树算法是adaboost算法的特殊情况
(二)使用平方误差的回归问题提升树:
输入:训练数据集T = {(x1,y1),(x2,y2)…(xn,yn)},x,y都属于实数,即树可以表示为:
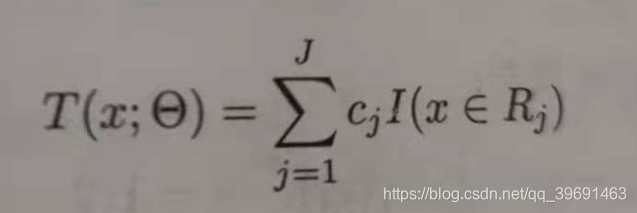
输出:提升树fm(x)
(1)初始化f0(x) = 0
(2)对于m = 1,2,…M.:
a:按照树公式,计算残差Rmi:(详情看证明)
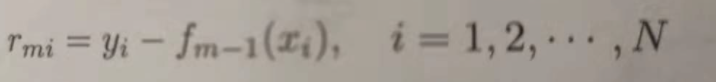
b:拟合残差Rmi学习一个回归树,得到T(x, θm)
c:更新fm(x) = fm-1(x)+T(x, θm)
(3)得到回归问题提升树
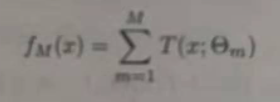
证明:回归问题的提升树只需要拟合当前模型fm-1(x)的残差
回归为题提升树采用前向分步算法:

(三)使用一般损失函数的一般决策问题的提升树–梯度提升树(大名鼎鼎的GBDT)
提升树采用加法模型和前向分步算法实现学习的优化过程,当损失函数为指数或者平方损失函数时候,其优化过程是简单的,但对于一般损失函数而言,其优化过程尤为复杂。针对这个问题,FREIDMAN提出了梯度提升树(gradient boosting decition tree ),这是利用最速下降法的近似方法,其关键是利用损失函数的负梯度在当前模型的值:
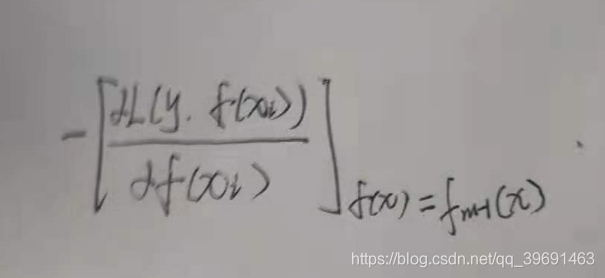
来作为回归问题提升树算法中的残差的近似值,从而拟合一个回归树。
GBDT实现步骤:

算法过程的特点:
- 算法每次迭代生成一颗新的决策树
- 计算损失函数对每个样本的一阶导和二阶导
- 通过贪心算法生成新的决策树,同时计算每个叶子节点的权重w
- 把新生成的决策树f(x)添加到模型中
GBDT的正则化方法:
1,第一种就是和adboost算法一样的正则化项,即设置步长,定义为v,对于弱学习器的迭代:

加上正则化项以后则有:
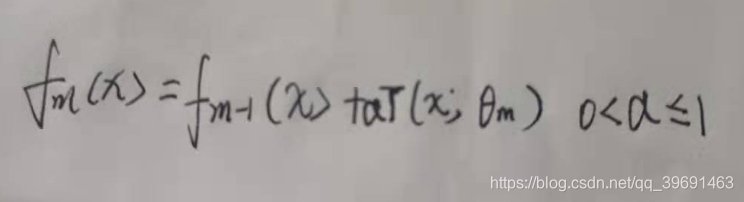
在同样的训练集上,较小的v就意味着弱学习器需要更多的迭代次数,通常我们用步长和最大迭代次数来决定算法的拟合效果。
2,第二种就是通过子采样比例,取值范围为(0,1】注意这里的采样和随机森林采样方式不同,随机森林是有放回的采样,这里是不放回抽样。设取值为x,当x= 1时候,即所有样本都可参与训练,等于没抽样,相同,如果x = 0,也等于没抽样,当0<x<1时,则只有部分样本会参与GBDT的决策树拟合。当x<1时候,会减少模型的方差,防止过拟合,但是会增加模型的偏差,因此取值不能太低,通常取值为【0.5,0.8】
使用了子采样的GBDT有时也称作随机梯度提升树(Stochastic Gradient Boosting Tree, SGBT)。由于使用了子采样,程序可以通过采样分发到不同的任务去做boosting的迭代过程,最后形成新树,从而减少弱学习器难以并行学习的弱点。
3,第三种就是对cart进行正则化剪枝。
GBDT的优缺点:
GBDT的主要优点有
1,能灵活的拟合各类数据,连续值和离散值都行
2,当采用一些健壮的损失函数时,对异常值的鲁棒性较强,比如 Huber损失函数和Quantile损失函数。更多损失函数可参考该文档
3,在相对较少的调参时间情况下,预备的准确率也较高。这个问题有一个经典的面试问答
GBDT的主要缺点有:
1)由于弱学习器之间存在依赖关系,难以并行训练数据。不过可以通过自采样的SGBT来达到部分并行