[数据结构与算法]决策树学习笔记

一、概念

在树的结点处按照属性的不同条件对样本进行划分。

二、决策树的生成

1. 特征的选择：局部最优

选择最优属性的最优划分。

度量结点的不确定程度：熵、基尼系数、分类错误率。

结点越不纯，结点处类分布越平衡，值越大。

$Entropy(t)=?{\sum }_{k=0}^{K}p(k|t)log(p(k|t))$

$Gini(t)=1?{\sum }_{k=0}^K[p(k|t){]}^2$

$ClassificationError=1?max[p(k|t)]$

比较分裂前后不纯程度的差别

信息增益（ID3）：分裂前后结点熵的差

$\Delta =I(parent)?I(children)$

$I(children)={\sum }_{j=0}^V\frac{N(v_j)}{N}H(v_j)$

$v$是分裂后的结点

信息增益率（C4.5）：考虑分裂后得到的结点数量。不希望输出的结点过多，会过拟合。
$Gainratio=\frac{\Delta }{splitInfo}$
$splitInfo=?{\sum }_{i=1}^{K}p(v_i)logp(v_i)$

对分类型特征，直接按照特征类别进行划分，计算划分前后的信息增益，选择信息增益最大的最优特征

对连续型特征，选择适当的划分点：

• 方法一：采用穷举法，遍历$N$个样本的特征值，每个特征值做一次划分点，统计小于它的样本和大于它的样本。时间复杂度$O(N^2)$

• 方法二：首先对特征值进行排序，然后选择两个特征值之间的中间
  

2. 何时停止分裂

• 结点处所有样本同属一类。
• 样本熵小于某个阈值（基本属于同一类）
• 结点处所有样本特征值相同（无更多特征可以选择）：返回比例最高的类
• 信息增益小于某个阈值（提前剪枝）：返回父节点中比例最高的类
• 结点处样本数小于某个阈值：返回父节点中比例最高的类

3. 决策树的剪枝

剪枝时考虑整体的损失函数

$|T|$表示叶节点的数量

$C_{\alpha }(T)=C(T)+\alpha |T|$

剪枝算法：

递归地从叶节点向上回缩，若回缩后树的损失函数值小于等于回缩前，则进行剪枝

4.CART(Classification and Regression Tree)的生成与剪枝

回归树：平方误差最小化

对每个切分点，划分两个区域

损失函数有

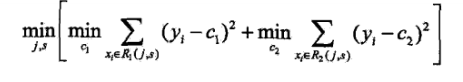
其中

遍历所有特征，找到最优特征$j$和对应的切分点$s$

分类树：按照基尼系数选择最优特征。

CART要生成尽量大的树，结束的标准是结点处样本数小于某个阈值 / Gini系数小于某个阈值。

CART剪枝

CART剪枝算法确定了$\alpha$和最优子树。

原理：当$\alpha$从小增大，${\alpha }_0$<${\alpha }_1$<${\alpha }_2$<…，产生的一系列区间[${\alpha }_i$, ${\alpha }_{i+1}$)，每个区间内都对应一个最优子树。最优子树序列$T_0$,$T_1$,$T_2$…是嵌套的。

某个结点剪枝前后损失相同，即

$C$($T_0$)+$\alpha$ = $C$($T_1$)+$\alpha$|$T_1$|

$\alpha$ = $\frac{C(T_0)?C(T_1)}{|T_1|?1}$

对每一个结点计算$\frac{C(T_0)?C(T_1)}{|T_1|?1}$并设为${\alpha }_1$，则剪枝后的T_1即为[${\alpha }_1$, ${\alpha }_2$)中的最优子树。

利用验证集在$T_0$,$T_1$,$T_2$…中寻找最优决策树（平方误差或基尼指数小的），$T_k$确定，对应的${\alpha }_k$也确定了。

三、 决策树的性质

• 不需要先验假设。
• 对未知样本分类速度快，最多为树的深度。
• 解释性强，可以得到各个特征的重要程度。
• 对样本噪声的抗干扰性强。
• 对冗余特征的抗干扰性强，但会受到不相干特征的影响。
• 当样本小特征多时，易添加一些欺骗性结点。特别是当模型拓展到一定深度时。