[数据结构与算法]二叉树的遍历

关于二叉树的算法问题，一般都以二叉树的遍历为基础，这里给出二叉树的多种遍历方式

树结构：

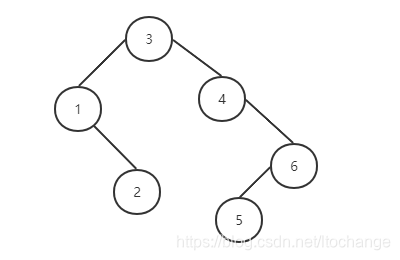
树结点的定义及其构建：

class TreeNode:
    def __init__(self, x):
        self.val = x
        self.left = None
        self.right = None
# 构建
root = TreeNode(3)
a = TreeNode(1)
b = TreeNode(4)
c = TreeNode(2)
d = TreeNode(6)
e = TreeNode(5)
root.left = a
root.right = b
a.right = c
b.right = d
d.left = e

前序遍历preorder

又叫深度优先遍历（dfs），访问顺序：根-左-右，返回[3, 1, 2, 4, 6, 5]

递归实现：

class Solution:
    def preorderTraversal_recur(self, root: TreeNode):
        if not root:
            return []
        res_li = []
        res_li.append(root.val)
        left = self.preorderTraversal_recur(root.left)
        right = self.preorderTraversal_recur(root.right)
        res_li.extend(left)
        res_li.extend(right)
        return res_li

非递归实现：

class Solution:
    def preorderTraversal(self, root: TreeNode):
        stack = [root]
        res_li = []
        while len(stack) > 0:
            r = stack.pop()
            if r:
                res_li.append(r.val)
                stack.append(r.right)
                stack.append(r.left)
        return res_li

中序遍历inorder

访问顺序：根-左-右，返回[1, 2, 3, 4, 5, 6]

递归实现：

class Solution:
     def inorderTraversal_recur(self, root: TreeNode):
        if not root:
            return []
        res_li = self.inorderTraversal_recur(root.left)
        res_li.append(root.val)
        right = self.inorderTraversal_recur(root.right)
        res_li.extend(right)
        return res_li

非递归实现：

class Solution:
    def inorderTraversal(self, root: TreeNode):
        stack = []
        res_li = []
        p = root
        while stack or p:
            if p:
                stack.append(p)
                p = p.left
            else:
                p = stack.pop()
                res_li.append(p.val)
                p = p.right
        return res_li

后序遍历postorder

访问顺序：左-右-根，返回结果[2, 1, 5, 6, 4, 3]

递归实现：

class Solution:
      def postorderTraversal_recur(self, root: TreeNode):
        if not root:
            return []
        res_li = self.postorderTraversal_recur(root.left)
        right = self.postorderTraversal_recur(root.right)
        res_li.extend(right)
        res_li.append(root.val)
        return res_li

非递归实现：

class Solution:
      def postorderTraversal(self, root: TreeNode):
        # 后序遍历，左右根，转化为根右左的倒序
        stack = [root]
        res_li = []
        while len(stack) > 0:
            r = stack.pop()
            if r:
                res_li.append(r.val)
                stack.append(r.left)
                stack.append(r.right)
        res_li.reverse()
        return res_li

层序遍历

又叫广度优先遍历（bfs），逐层遍历结点，返回结果[3, 1, 4, 2, 6, 5]

class Solution:
    def levelOrder(self, root: TreeNode):
        # 层序遍历用队列实现
        stack = [root]
        res_li = []
        while len(stack) > 0:
            r = stack.pop(0)
            # 从另一边出
            if r:
                res_li.append(r.val)
                stack.append(r.left)
                stack.append(r.right)
        return res_li