数据结构与算法学习笔记 之 程杰《大话数据结构》
第一章 数据结构绪论
- 数据项:数据不可分割的最小单位。在数据结构课程中,把数据项定义为最小单位,有助于我们更好地解决问题。但是真正讨论问题时,数据元素才是数据结构中建立数据模型的着眼点。
- 数据对象:是性质相同的数据元素的集合,是数据的子集。其中,性质相同是指数据元素具有相同数量和类型的数据项。
- 结构:各个组成部分相互搭配和排列的方式。
- 数据结构:相互之间存在一种或多种特定关系的数据元素的集合。
- 数据类型:是指一组性质相同的值的集合及定义在此集合上的一些操作的总称。
第二章 算法
-
算法的设计要求:正确性、可读性、健壮性、高效率和低存储量。
-
算法的特征:有穷性、确定性、可行性、输入、输出。
-
最终,在分析程序的运行时间时,最重要的是把程序看成是独立于程序设计语言的算法或一系列步骤。
-
在分析一个算法的运行时间时,重要的是把基本操作的数量与输入规模关联起来,即基本操作的数量必须表示成输入规模的函数。
-
算法时间复杂度:在进行算法分析时,语句总的执行次数T(n)是关于问题规模n的函数,进而分析T(n)随n的变化情况并确定T(n)的数量级。算法的时间复杂度,也就是算法的时间量度,记作:T(n)=O(f(n)),它表示随问题规模n的增大,算法执行时间的增长率和f(n)的增长率相同,称作算法的渐进时间复杂度,简称为时间复杂度。【注:这种用大写O()来体现时间复杂度的记法,称为大O记法】
-
推导大O阶:(1) 用常数1取代运行时间中的所有加法常数 (2) 在修改后的运行次数函数中,只保留最高阶项 (3) 如果最高阶项存在且不是1,则去除与这个项相乘的常数。得到的结果就是大O阶。
-
常用的时间复杂度所耗费的时间从小到大依次是:
O(1) < O(logn) < O(n) < O(nlogn) < O(n^2) < O(n^3) < O(2^n) < O(n!) < O(n^n)
-
对算法的分析,一种方法是计算所有情况的平均值,这种时间复杂度的计算方法称为平均时间复杂度。另一种方法是计算最坏情况下的时间复杂度,这种方法称为最坏时间复杂度。一般在没有特殊说明的情况下,都是指最坏时间复杂度。
-
算法的空间复杂度通过计算算法所需的存储空间实现,算法空间复杂度的计算公式记作:S(n)=O(f(n)),其中,n为问题的规模,f(n)为语句关于n所占存储空间的函数。
第三章 线性表
-
数组的长度是存放线性表的存储空间的长度,存储分配后一般不变;线性表的长度是线性表中数据元素的个数,是变化的。
-
“->” 主要用于指向结构体、C++中的class等含有子数据的指针用来取子数据。
struct Data
{
int a,b;
};
struct Data* p; //定义结构体指针
struct Data A = {1,2};
p = &A;
int x;
x = p->a; //取出p所指向的结构体中,包含的数据项a赋值给x
//由于 p->a==A.a, 故 x=1
- 线性表的顺序存储结构:在存、读数据时,不管是哪个位置,时间复杂度都是O(1) ; 而插入或删除数据时,时间复杂度都是O(n)。这就说明,它比较适合元素个数不太变化,而更多是存取数据的应用。
- 线性表的链式存储结构:
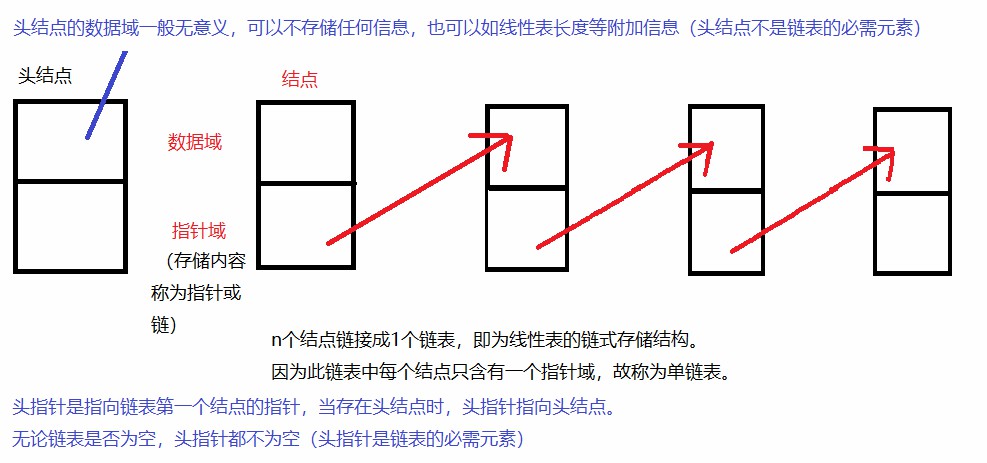
(1)假设 p 是指向线性表第 i 个元素的指针,则用 p->data 表示结点 ai 的数据域,p->data 的值是一个数据元素,而结点 ai 的指针域可以用 p->next 来表示,p->next 的值是一个指针,指向第 i+1 个元素。综上有:若 p->data = ai,则 p->next->data = a(i+1)
(2)单链表的读取:(核心思想:工作指针后移)
//初始条件:顺序线性表L已存在,1<=i<=ListLength(L)
Status GetElem(LinkList L,int i,ElemType *e)
{
LinkList p;
p=L->next; //声明一结点p,指向链表L的第一个结点
int j=1;
//p 不为空或者 j还没有等于i时,循环继续
while (p && j<i)
{
p=p->next; //让p指向下一个结点
++j;
}
if (!p || j>i)
return ERROR;
*e=p->data; //取第i个元素的数据
}
要读取第 i 个元素,需要遍历 i-1 次。
- 单链表的插入与删除:
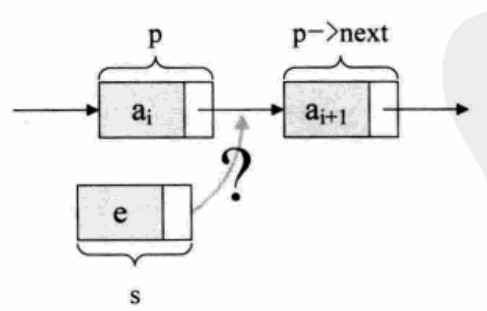
s->next = p->next;
p->next = s;
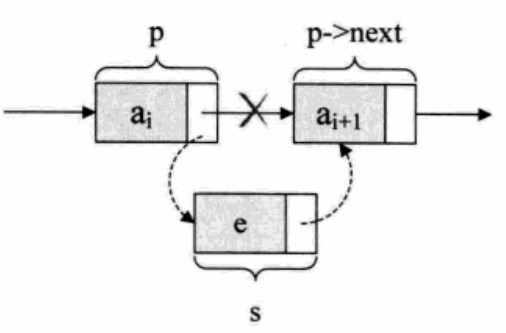
对于单链表的表头和表尾的特殊情况,操作相同:
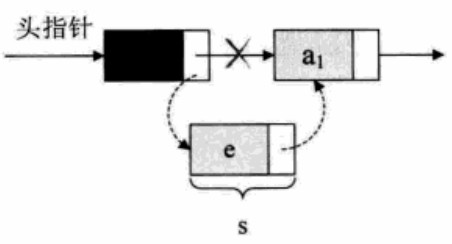
//单链表第i个数据插入结点
Status ListInsert(LinkList *L,int i,ElemType e)
{
LinkList p,s;
p = *L; //声明一结点p指向链表第一个结点
int j=1;
//p 不为空或者 j还没有等于i时,循环继续
while (p && j<i)
{
p = p->next; //将后一个结点的指针域赋给p
++j;
}
if (!p || j>i)
return ERROR;
s = (LinkList)malloc(sizeof(Node)); //生成新结点
s->data = e;
s->next = p->next;
p-next = s;
}
- 单链表的删除:
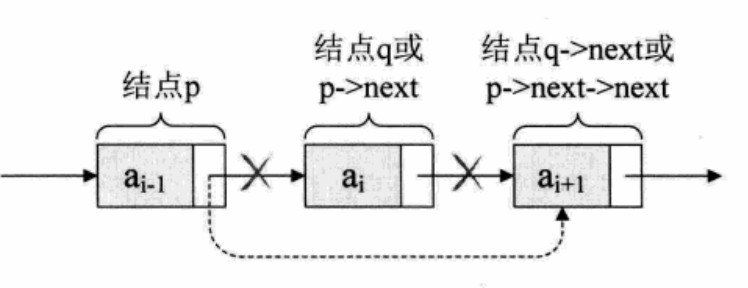
q = p->next;
p->next = q->next;
//单链表第 i 个数据删除
Status ListDelete(LinkList *L,int i,ElemType *e)
{
LinkList p,q;
p = *L;
int j=1;
//只要 p->next 不是指向空,而且j<i,就继续循环
while (p->next && j<i)
{
p = p->next;
++j;
}
//如果 p->next 指向空或 j>i
//注意理解为什么是判断p->next是否为空,因为p=*L是头指针,指向的是头结点而非第一个结点
if (!(p->next) || j>i)
return ERROE; //第 i 个元素不存在
q = p->next;
p->next = q->next; //q 相当于一个过渡结点
*e = q->data;
free(q); //让系统回收过渡结点,释放内存
}
- 单链表的整表创建:
//随机产生n个元素的值,建立带头结点的单链线性表L(头插法)
void CreateListHead(LinkList *L,int n)
{
LinkList p;
int i;
srand(time(0)); //初始化随机数种子
*L = (LinkList)malloc(sizeof(Node));
//让L的头结点的指针指向NULL,即建立一个带头结点的单链表
(*L)->next = NULL;
for (i=0;i<n;i++)
{
p = (LinkList)malloc(sizeof(Node)); //生成新结点
p->data = rand()%100+1; //随机生成100以内的数字
p->next = (*L)->next;
(*L)->next = p; //插入到表头
}
}
//随机产生n个元素的值,建立带头结点的单链线性表L(尾插法)
void CreateListTail(LinkList *L,int n)
{
LinkList p,r;
int i;
srand(time(0));
*L = (LinkList)malloc(sizeof(Node));
r = *L; //r为尾结点,r会随着循环不断变化结点
for (i=0;i<n;i++)
{
p = (Node*)malloc(sizeof(Node)); //生成新结点
p->data = rand()%100+1;
r->next = p;
r = p; //循环改变r,保证r为尾结点
}
//循环结束,将链表的尾结点指针域置空,以便之后遍历时确定尾部
r->next = NULL;
}
- 单链表的整表删除:
Status ClearList(LinkList *L)
{
LinkList p,q;
p = (*L)->next; //p指向第一个结点
while (p) //没到表尾
{
q = p->next;
free(p);
p = q;
}
(*L)->next = NULL; //头结点指针域置空
}
- 单链表结构与顺序存储结构总结:
(1)若线性表需要频繁查找,很少进行插入和删除操作,宜采用顺序存储结构;若需要频繁插入和删除,宜采用单链表结构。
(2)当线性表中的元素个数变化较大或者根本不知道有多少时,最好用单链表结构,因为这样不需要考虑存储空间的大小问题;而如果事先知道线性表的大致长度,用顺序存储结构效率更高。
- 静态链表:
(1)用数组描述的链表称为静态链表
(2)总的来说,静态链表其实是为了给没有指针的高级语言设计的一种实现单链表能力的方法。
- 循环链表:
(1)将单链表中终端结点的指针端由空指针改为指向头结点,就使整个单链表形成一个环,这种头尾相接的单链表称为单循环链表,简称循环链表
(2)为了使空链表与非空链表的处理一致,我们通常设一个头结点。但并非说循环链表一定要有头结点
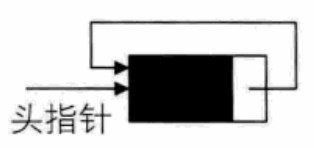

(3)在单链表中,拥有头结点,可以用O(1)的时间访问第一个结点,但对于尾结点的访问,却需要O(n)时间;而使用指向终端结点的尾指针来表示循环链表,查找第一个结点和终端结点都很方便
(4)利用尾指针rear 将两个循环链表合并:
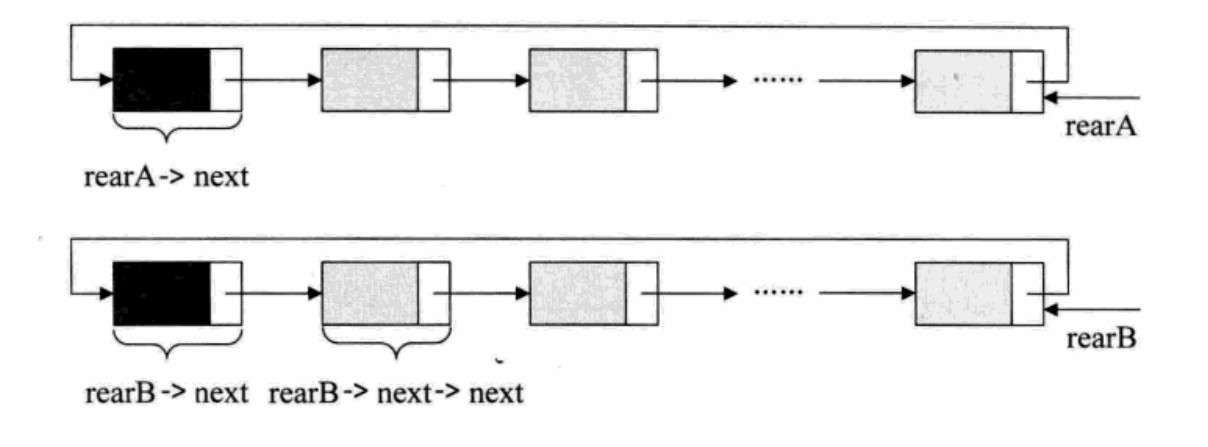
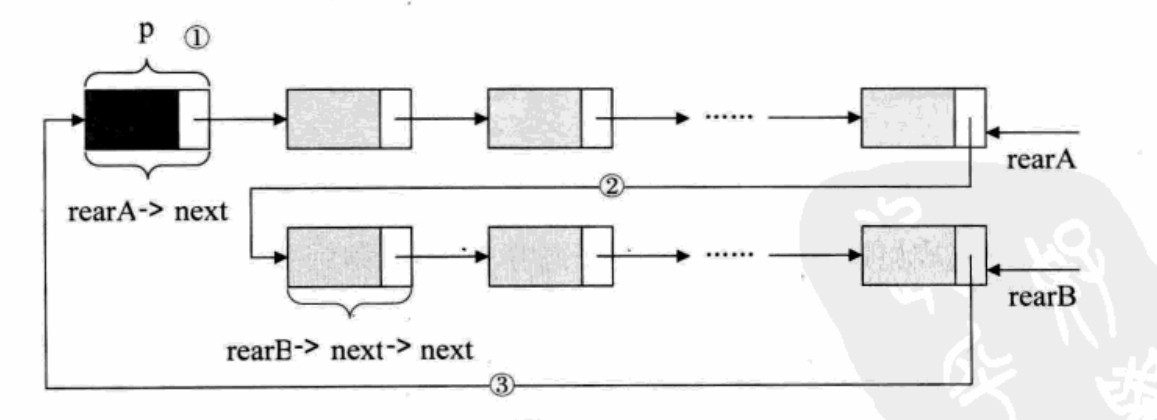
p = rearA->next; //保存A表的头结点
rearA->next = rearB->next->next; //将原指向B表的第一个结点(非头结点)赋值给 rearA->next
rearB->next = p; //将原A表的头结点赋值给 rearB->next
free(p);
- 双向链表:
(1)双向链表是在单链表的每个结点中,再设置一个指向其前驱结点的指针域

(2)双向链表的插入:
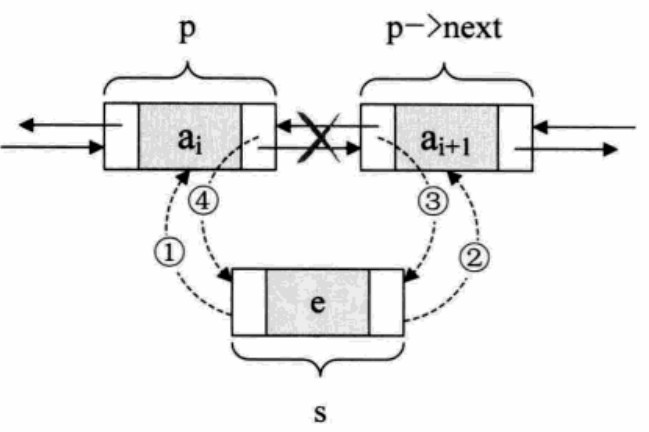
//顺序是关键:先搞定s的前驱和后继,再搞定后结点的前驱,最后解决前结点的后继
s->prior = p;
s->next = p->next;
p->next->prior = s;
p->next = s;
(3)双向链表的删除:
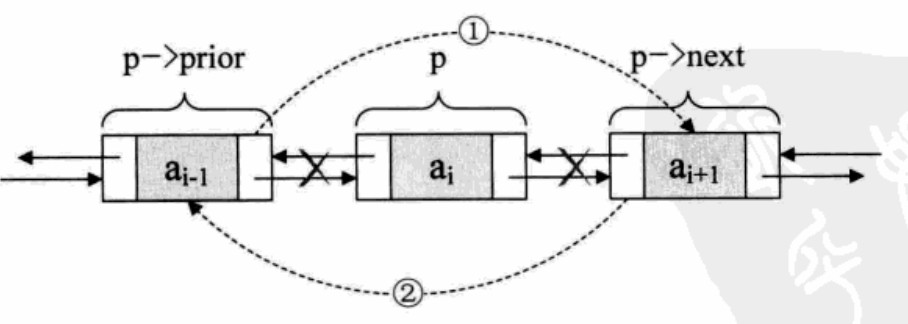
p->prior->next = p->next;
p->next->prior = p->prior;
free(p);
(4)总结:
双向链表相对于单链表来说会更加复杂,由于需记录两份指针,所以在空间上占用较多。不过,由于良好的对称性,它对某个结点的前后结点的操作更加方便,可以有效提高算法的时间性能(用空间换时间)。
? (未完待续…)