排序算法 C/C++
从前有个王国,国王骄奢无度,贪图女色,后宫佳丽三千,但还是动用大量财力物力在全国范围内招妃纳妾,浸淫于女色之中。

又是一年的选妃开始,今年国王对身高比较敏感,要求这些候选者按照从低到高的顺序排列,供其选择。。。
宫廷首席太监小桂子于是命令所有小公公把宫女的身高都量出来并上报到他处,然后命令身为太监伴读小书童的你帮他按身高大小排好序,数据如下:
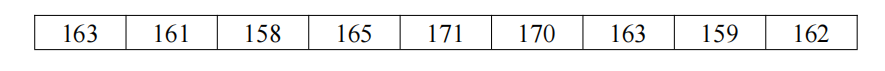
常用排序算法 C语言实现
选择排序
第一步 先找出所有候选美女中身高最高的,与最后一个数交换
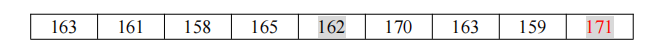
第二步 再找出除最后一位美女外其它美女中的最高者,与倒数第二个美女交换位置

第三步 再找出除最后两位美女外其它美女中的最高者,与倒数第三个美女交换位置,因为倒数 第三个本身已是最大的,所以实际无需交换.

。。。 。。。重复以上步骤,直到最后只剩下一人,此时,所有的美女均已按照身高由矮到高的 顺序排列

#include <stdio.h>
#include <stdlib.h>
void swap(int *num1,int *num2) //交换两个变量的值 {
int temp = *num1;
*num1 = *num2;
*num2 = temp;
} void SelectSort1(int arr[], int len)
{
for( int i=0; i<len-1; i++)
{
int max = 0;
for(int j=1; j<len-i; j++)
{
//查找未排序的元素
if(arr[j]>arr[max]) //找到目前最小值
{
max = j;
}
}//printf("max: %d beauties %d\n", max,len-i-1);
if(max != (len-i-1))
{
swap(&arr[max], &arr[len-i-1]);
}
}
}
void SelectSort2(int arr[], int len)
{
int i,j;
for (i = 0 ; i < len - 1 ; i++)
{
int min = i;
for (j = i + 1; j < len; j++)
{
//查找未排序的元素
if (arr[j] < arr[min]) //找到目前最小值
{
min = j; //记录最小值 }
}
swap(&arr[min], &arr[i]); //交换
}
}
int main(void)
{
int beauties[]= {163, 161, 158, 165, 171, 170, 163, 159, 162};
int len = sizeof(beauties)/sizeof(beauties[0]);
/*for( int i=0; i<len-1; i++)
{
int max = 0;
for(int j=1; j<len-i; j++)
{
if(beauties[j]>beauties[max])
{
max = j;
}
}
printf("max: %d beauties %d\n", max,len-i-1);
if(max != (len-i-1))
{
swap(&beauties[max], &beauties[len-i-1]);
}
}*/
SelectSort2(beauties, len);
for(int i=0; i<len; i++)
{
printf("%d ", beauties[i]);
}
system("pause");
}
冒泡排序
每当皇帝选妃时,首席太监小桂子总是忍不住在旁边偷窥这些候选的美女,有一次他发现做 为伴读小书童的你居然犯了个常人都可以轻易看出的错误,有几位候选的美女站成如下一排:

当我们采用前面的选择排序时,我们仍然要将候选者遍历 5 遍,才能完成最终的排序,但其 实,本身这些美女出了第一个外,已经很有序了,我们只需要把第一个和第二个交换,然后又和 第三个交换,如此循环,直到和最后一个交换后,整个数组基本就有序了!
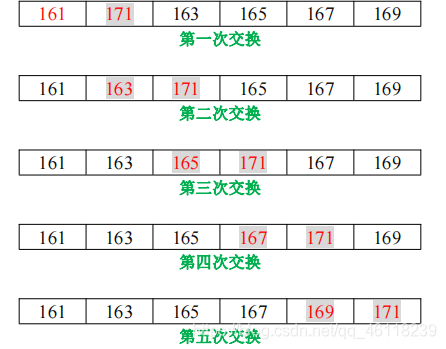
当然,并不是每次都这么幸运,像下面的情况就会更复杂一些,一趟并不能完全解决问题, 我们需要多趟才能解决问题.

经过上述五步后,得到的结果:

此时,我们只保障了最后一个数是最大的, 并不能保障前面的数一定会有序,所以,我们继续按 照上面五步对剩下的 5 个数继续进行一次排序,数组就变得有序了.
以上过程就是冒泡排序: 通过重复地遍历未排序的数列,一次比较两个元素,如果它们的顺 序错误就把它们交换过来。走访数列的工作是重复地进行直到没有再需要交换,也就是说该数列 已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢得像泡泡一样“浮”到数 列的顶端,故而得名!
#include <stdio.h>
#include <stdlib.h>
void swap(int* num1, int* num2) //交换两个指针所指向得的元素的值
{
int temp = *num1;
*num1 = *num2;
*num2 = temp;
}
void BubbleSort(int arr[], int len)
{
for (int i = 0; i < len - 1; i++)
{
bool sorted = true;
for (int j = 0; j < len - 1 - i; j++)
{
if (arr[j] > arr[j + 1])
{
swap(&arr[j], &arr[j + 1]); //if(sorted) break;
sorted = false;
}
}
if (sorted) break;
}
}
int main(void)
{
int beauties[] = { 163, 161, 158, 165, 171, 170, 163, 159, 162 };
int len = sizeof(beauties) / sizeof(beauties[0]);
BubbleSort(beauties, len);
printf("美女排序以后的结果是:\n");
for (int i = 0; i < len; i++)
{
printf("%d ", beauties[i]);
}
system("pause");
return 0;
}
插入排序
自从上次小桂子发现了冒泡排序后,他开始相信自己的聪明才智比伴读小书童居然要高,所以 他更加热衷于排序算法研究了,没事的时候, 时不时找几个宫女演练一下,这时他又发现了一个新 的排序方式,对于一下宫女们的队列:

-
首先, 我们只考虑第一个元素,从第一个元素 171 开始,该元素可以认为已经被排序;

-
取下一个元素 161 并记录,并让 161 所在位置空出来,在已经排序的元素序列中从后向前扫 描;

-
该元素(171)大于新元素,将该元素移到下一位置;

-
171 前已经没有最大的元素了, 则将 161 插入到空出的位置

-
取下一个元素 163,并让 163 所在位置空出来,在已经排序的元素序列中从后向前扫描;

-
该元素(171)大于新元素 163,将该元素移到下一位置

-
继续取 171 前的元素新元素比较, 直到找到已排序的元素小于或者等于新元素的位置;新 元素大于 161,则直接插入空位中

-
重复步骤 2~7,直到完成排序

插入排序: 它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描, 找到相应位置并插入。插入排序在实现上,通常采用 in-place 排序(即只需用到 O(1)的额外空间 的排序),因而在从后向前扫描过程中,需要反复把已排序元素逐步向后挪位,为最新元素提供 插入空间
具体算法描述如下:
- 从第一个元素开始,该元素可以认为已经被排序;
- 取出下一个元素,在已经排序的元素序列中从后向前扫描;
- 如果该元素(已排序)大于新元素,将该元素移到下一位置; 重复步骤 3,直到找到已排序的元素小于或者等于新元素的位置;
- 将新元素插入到该位置; 重复步骤 2~5。
#include <stdio.h>
#include <stdlib.h>
void InsertSort(int arr[], int len) //插入排序
{
int preIndex = 0, current = 0;
for(int i=1; i<len; i++)
{
preIndex = i - 1;
current = arr[i];
while(preIndex >= 0 && arr[preIndex] > current)
{
arr[preIndex + 1] = arr[preIndex];
preIndex--;
}
arr[preIndex + 1] = current;
}
}
int main(void)
{
int beauties[]= {163, 161, 158, 165, 171, 170, 163, 159, 162};
int len = sizeof(beauties)/sizeof(beauties[0]);
InsertSort(beauties, len);
printf("美女排序以后的结果是:\n");
for(int i=0; i<len; i++)
{
printf("%d ", beauties[i]);
}
system("pause");
return 0;
}
希尔排序
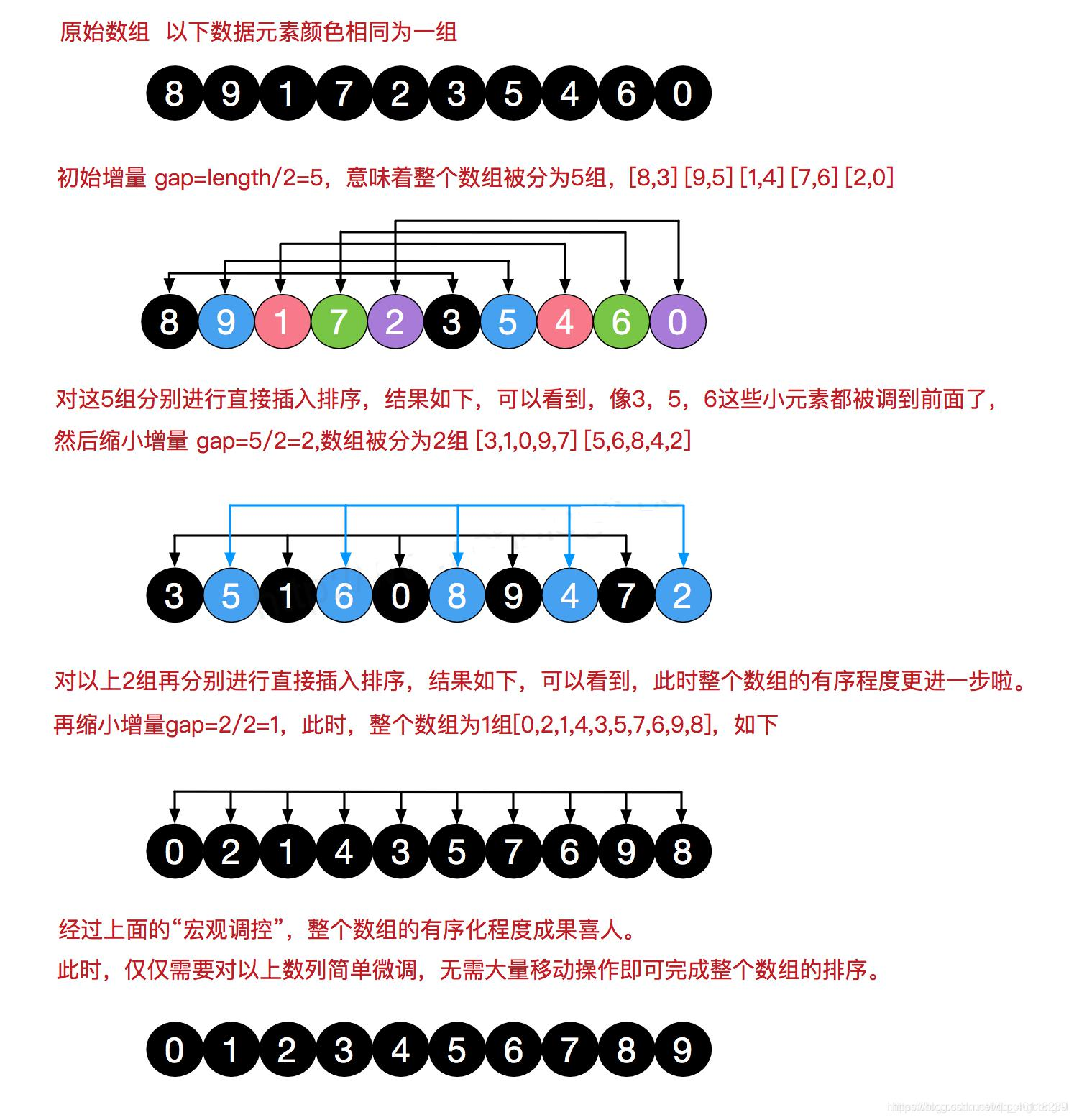
插入排序虽好,但是某些特殊情况也有很多缺点,比如像下面这种情况:

169 前的元素基本不用插入操作就已经有序, 元素 1 和 2 的排序几乎要移动数组前面的所有 元素!!! 于是,有个老帅哥就提出了优化此问题的希尔排序!
希尔排序是希尔(Donald Shell)于 1959 年提出的一种排序算法。希尔排序也是一种插入排 序,它是简单插入排序经过改进之后的一个更高效的版本,也称为缩小增量排序。它与插入排序 的不同之处在于,它会优先比较距离较远的元素。
希尔排序是把记录按下表的一定增量分组,对每组使用直接插入排序算法排序;随着增量逐 渐减少,每组包含的元素越来越多,当增量减至 1 时,所有元素被分成一组,实际上等同于执行一 次上面讲过的插入排序,算法便终止。
希尔排序的基本步骤
选择增量 :gap=length/2,缩小增量:gap = gap/2
增量序列:用序列表示增量选择,{n/2, (n/2)/2, …, 1}
先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序,具体算法描述:
选择一个增量序列 t1,t2,…,tk,其中 ti>tj,tk=1;
按增量序列个数 k,对序列进行 k 趟排序;
每趟排序,根据对应的增量 ti,将待排序列分割成若干长度为 m 的子序列,分别对各子表进 行直接插入排序;
仅增量因子为 1 时,整个序列作为一个表来处理,表长度即为整个序列的长度
#include <stdio.h>
#include <stdlib.h>
void ShellSort(int arr[], int len) //希尔排序
{
int gap = len/2;
for(; gap > 0; gap=gap/2) //增量,依次按除 2 的范围缩小
{
for(int i=gap; i<len; i++)
{
int current = arr[i];
int j = 0;
for(j=i-gap; j>=0 && arr[j] > current; j-=gap)
{
arr[j + gap] = arr[j];
}
arr[j + gap] = current;
}
}
}
int main(void)
{
int beauties[]= {163, 161, 158, 165, 171, 170, 163, 1, 2};
int len = sizeof(beauties)/sizeof(beauties[0]);
ShellSort(beauties, len);
printf("美女排序以后的结果是:\n");
for(int i=0; i<len; i++)
{
printf("%d ", beauties[i]);
}
system("pause");
return 0;
}
堆排序
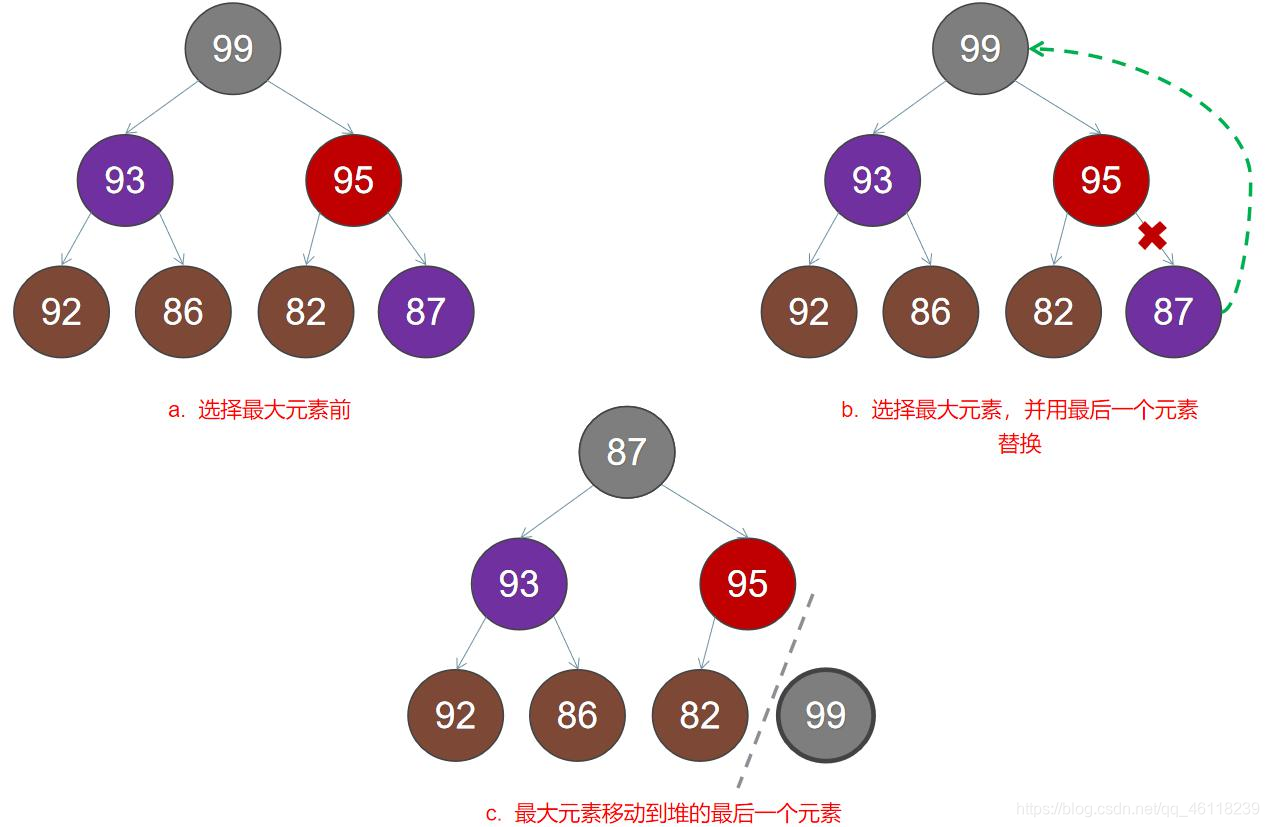
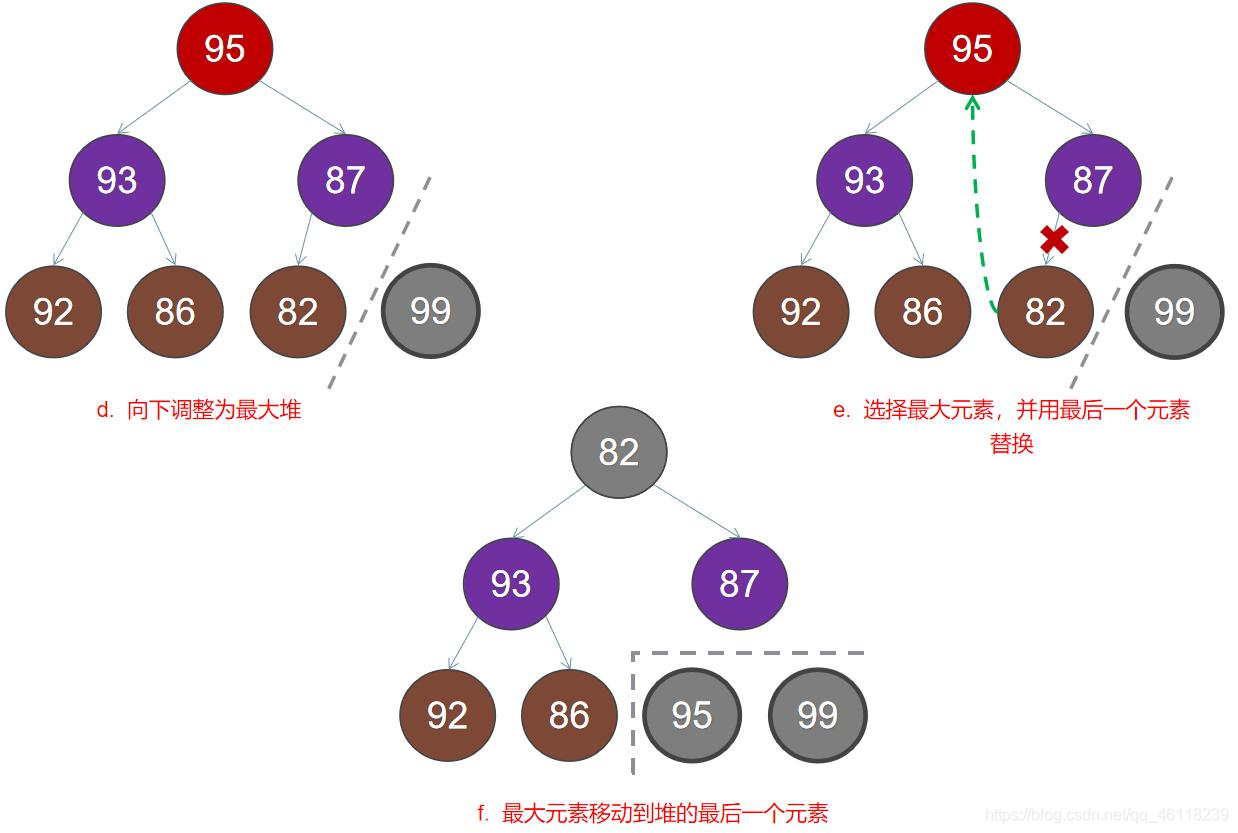
堆排序(Heapsort)是指利用堆这种数据结构所设计的一种排序算法,它是选择排序的一种。可以利用数组的特点快速定位指定索引的元素.
(选择排序工作原理 - 第一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,然后再从剩余的未排序元素中寻找到最小(大)元素,然后放到已排序的序列的末尾。以此类推,直到全部待排序的数据元素的个数为零)
其排序核心实现如下:
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
typedef struct _Heap
{
int *arr; //存储堆元素的数组
int size; //当前已存储的元素个数
int capacity; //当前存储的容量
} Heap;
bool initHeap(Heap &heap, int *orginal, int size);
bool popMax(Heap &heap, int &value);
void heapSort(Heap &heap);
static void buildHeap(Heap &heap);
static void adjustDown(Heap &heap, int index);
/*初始化堆*/
bool initHeap(Heap &heap, int *orginal, int size)
{
//heap.arr = new int[capacity];
heap.arr = orginal;
if (!heap.arr) return false;
heap.capacity = size;
heap.size = size;
//如果存在原始数据则构建堆
if(size > 0)
{
//方式一: 直接调整所有元素
//建堆
buildHeap(heap);
}
return true;
}
/* 从最后一个父节点(size/2-1 的位置)逐个往前调整所有父节点(直到根节 点),
确保每一个父节点都是一个最大堆,最后整体上形成一个最大堆 */
void buildHeap(Heap &heap)
{
int i;
for (i = heap.size / 2 - 1; i >= 0; i--)
{
adjustDown(heap, i);
}
}
/*将当前的节点和子节点调整成最大堆*/
void adjustDown(Heap &heap, int index)
{
int cur = heap.arr[index];//当前待调整的节点
int parent, child;
/*判断否存在大于当前节点子节点,如果不存在 ,则堆本身是平衡的,不 需要调整;
如果存在,则将最大的子节点与之交换,交换后,
如果这个子节点还有子节 点,则要继续 按照同样的步骤对这个子节点进行调整 */
for (parent = index; (parent * 2 + 1)<heap.size; parent = child)
{
child = parent * 2 + 1;
//取两个子节点中的最大的节点
if (((child + 1)<heap.size) && (heap.arr[child]<heap.arr[child + 1]))
{
child++;
}
//判断最大的节点是否大于当前的父节点
if (cur >= heap.arr[child]) //不大于,则不需要调整,跳出循环
break;
}
else //大于当前的父节点,进行交换,然后从子节点位置继续向下调 整
{
heap.arr[parent] = heap.arr[child];
heap.arr[child] = cur;
}
}
}
/* 实现堆排序 */
void heapSort(Heap &heap)
{
if (heap.size<1) return ;
while(heap.size>0)
{
int tmp = heap.arr[0];
heap.arr[0] = heap.arr[heap.size-1];
heap.arr[heap.size-1] = tmp;
heap.size--;
adjustDown(heap, 0);// 向下执行堆调整
}
}
/* 删除最大的节点,并获得节点的值*/
bool popMax(Heap &heap, int &value)
{
if (heap.size<1) return false;
value = heap.arr[0];
heap.arr[0] = heap.arr[--heap.size];
//heap.arr[0] = heap.arr[heap.size-1];
//heap.size--;
adjustDown(heap, 0);// 向下执行堆调整
return true;
}
int main(void)
{
Heap hp;
int origVals[] = { 1, 2, 3, 87, 93, 82, 92, 86, 95 };
int i = 0;
if(!initHeap(hp, origVals, sizeof(origVals)/sizeof(origVals[0])))
{
fprintf(stderr, "初始化堆失败!\n");
exit(-1);
}
for (i = 0; i<hp.size; i++)
{
printf("the %dth element:%d\n", i, hp.arr[i]);
}
//执行堆排序
heapSort(hp);
printf("堆排序后的结果:\n");
for(i=0; i<sizeof(origVals)/sizeof(origVals[0]); i++)
{
printf(" %d", origVals[i]);
}
system("pause");
return 0;
}
归并排序
研究了这么多算法以后,小桂子颇有收获,基本自认为排序算法已经全部掌握,于是就想卖 弄一下自己的“算法内功”,另一方面为了交流推广,把这些算法传播出去,就召开一个全国算 法大赛,集思广益,征集更牛逼的算法!
在算法大赛上,有两位白发葱葱的老者提出的算法让小桂子自惭形秽,感叹良多。。。
其中一位叫归并长老的老者,提出了如下的排序方法:
当两个组数据已经有序,我们可以通过如下方式(以下简称归并大法)让两组数据快速有序

我们可以依次从两组中取最前面的那个最小元素依次有序放到新的数组中,然后再把新数组 中有序的数据拷贝到原数组中,快速完成排序

依靠这种思想,归并长老提出了如下的排序方法!
具体步骤
对于下面这一组待排序的数组
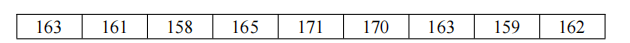
先以中间为界,把其均分为 A 和 B 两个数组(如果是奇数个,允许两组数相差一个)

如果 A 和 B 两组数据能够有序,则我们可以通过上面的方式让数组快速排好序。
此时,A 组有 4 个成员, B 组有 5 个成员, 但两个数组都无序,然后我们可以采用分治法继 续对 A 组和 B 组进行均分,以 A 组为例,又可以均分 A1 和 A2 两个组如下:
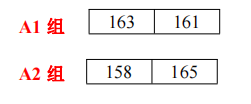
均分后,A1 组和 A2 组仍然无序,继续利用分治法细分,以 A1 组为例,A1 又可分成如下 两组

数组细分到一个元素后,这时候,我们就可以采用归并法借助一个临时数组将数组 A1 有序化! A2 同理!
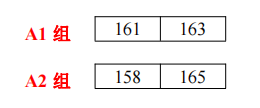
依次类推,将 A1 组和 A2 组归并成有序的 A 组, B 组同理!
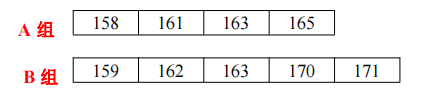
最后,将 A 和 B 组使用归并大法合并,就得到了完整的有序的结果!

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
void mergeAdd_demo(int arr[], int left, int mid, int right)
{
int temp[64]= {0};
int i = left; //指向左边数组最小的元素位置
int j = mid; //指向右边数组最小的元素位置
int k = 0; //临时数组的下标
while( i<mid && j<=right)
{
if(arr[i]<arr[j])
{
temp[k++] = arr[i++];
}
else
{
temp[k++] = arr[j++];
}
}
while(i< mid)
{
temp[k++] = arr[i++];
}
while(j<= right)
{
temp[k++] = arr[j++];
}
//把 temp 中的内容拷贝到 arr 数组中
memcpy(arr+left, temp, sizeof(int) * (right - left + 1));
}
void mergeAdd(int arr[], int left, int mid, int right, int *temp) //int temp[64]={0};
{
int i = left; //指向左边数组最小的元素位置
int j = mid; //指向右边数组最小的元素位置
int k = left; //临时数组的下标
while( i<mid && j<=right)
{
if(arr[i]<arr[j])
{
temp[k++] = arr[i++];
}
else
{
temp[k++] = arr[j++];
}
}
while(i< mid)
{
temp[k++] = arr[i++];
}
while(j<= right)
{
temp[k++] = arr[j++];
}//把 temp 中的内容拷贝到 arr 数组中
memcpy(arr+left, temp+left, sizeof(int) * (right - left + 1));
}
void mergeSort(int arr[], int left, int right, int *temp)
{
//归并排序
int mid = 0;
if(left < right)
{
mid = left +(right - left)/2;
mergeSort(arr, left, mid, temp);
mergeSort(arr, mid + 1, right, temp);
mergeAdd(arr, left, mid + 1, right, temp);
}
}
int main(void)
{
int beauties[]= {10, 11, 12, 13, 2, 4, 5, 8};
int len = sizeof(beauties)/sizeof(beauties[0]);
int *temp = new int[len];
{
{
//int mid = len/2;
mergeSort(beauties, 0, len - 1, temp); //mergeAdd(beauties, 0, mid, len-1, temp);
printf("执行归并大法后:\n");
for(int i=0; i<len; i++)
{
printf("%d ", beauties[i]);
}
system("pause");
return 0;
}
}
}
快速排序
接上面的故事未完待续,除了归并长老外,还有另外一位叫快速长老的快速大法也是被小桂 子赞不绝口,大呼奇妙!这位快速长老的算法思想时这样的:
- 每次选取第一个数为基准数
- 然后使用“乾坤挪移大法”将大于和小于基准的元素分别放置于基准数两边;
- 继续分别对基准数两侧未排序的数据使用分治法进行细分处理,直至整个序列有序。
对于下面待排序的数组:
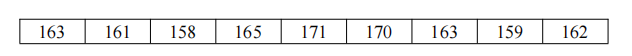
第一步:先选择第一个数 163 为基准数,以 163 为基准将小于它的数排在它前面,大于等于它 的数排在其后,结果如下:

此处,快速长老介绍了具体排列数据的步骤
- 确定 163 为基准数后,先把 163 从数组中取出来

- 然后从最右端开始,查找小于基准数 163 的数,找到 162,将其移至空出来的元素中,

- 接下来,从最左边未处理的元素中从左至右扫描比基数 163 大的数,将其移动至右侧空出来的元素中
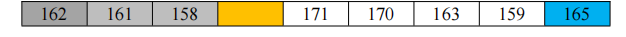
- 接下来,继续从最右边未处理的元素中从右至左扫描比基数 163 小的数,将其移动至左侧 空出来的元素中

接下来再重复执行步骤 3,171 执行右移

重复执行步骤 4,此时右边的值已经均大于基数,左边的值均已小于基数

接下来我们将基数保存回黄色空格中

第二步:采用分治法分别对基数左边和右边的部分运用第一步中的方法进行递归操作,直到整个 数组变得有序,以左边的数组为例:

选择 162 为基数,运用“乾坤挪移大法”得到结果如下:

以 162 为界,把数组分成两个部分,此时,基数右侧已经没有数据,所以,接下来只要继续对左侧的数组分治处理即可,选择 159 为基数,再次运用“乾坤挪移大法”得到结果如下:
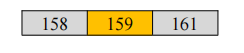
#include <stdio.h>
#include <stdlib.h>
int partition(int arr[], int low, int high)
{
int i = low;
int j = high;
int base = arr[low];
if(low < high)
{
while(i < j)
{
while(i < j && arr[j] >= base)
{
j--;
}
if(i < j) //右边已经找到小于基数的数
{
arr[i++] = arr[j];
}
while(i < j && arr[i] < base)
{
i++;
}
if( i < j) //左边已经找到大于基数的数
{
arr[j--] = arr[i];
}
}
arr[i] = base;
}
return i;
}
void QuickSort(int *arr, int low, int high) //实现快速排序
{
if(low < high)
{
int index = partition(arr, low, high);
QuickSort(arr, low, index-1);
QuickSort(arr, index+1, high);
}
}
int main(void)
{
int arr[] = {163, 161, 158, 165, 171, 170, 163, 159, 162};
int len = sizeof(arr)/sizeof(arr[0]);
/*int index = partition(arr, 0, len-1); printf("分区完毕, 基数下标: %d\n", index); */
QuickSort(arr, 0, len-1);
printf("执行快速排序后的结果:\n");
for(int i=0; i<len; i++)
{
printf(" %d", arr[i]);
}
system("pause");
return 0;
}
排序算法应用分析
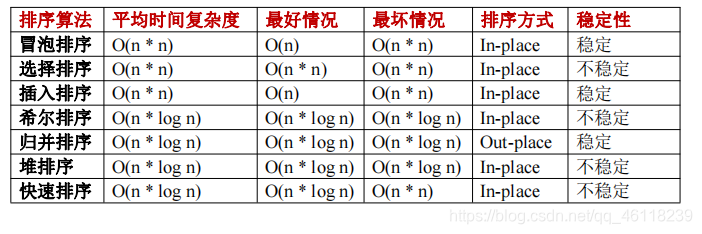
常用排序算法(C++)
以下是一些最基本的排序算法。虽然在 C++ 里可以通过 std::sort() 快速排序,而且刷题时很少需要自己手写排序算法,但是熟习各种排序算法可以加深自己对算法的基本理解,以及解出由这些排序算法引申出来的题目。
快速排序(Quicksort)
我们采用左闭右闭的二分写法。
void quick_sort(vector<int> &nums, int l, int r)
{
if (l + 1 >= r)
{
return;
}
int first = l, last = r - 1, key = nums[first];
while (first < last)
{
while(first < last && nums[last] >= key)
{
--last;
}
nums[first] = nums[last];
while (first < last && nums[first] <= key)
{
++first;
}
nums[last] = nums[first];
}
nums[first] = key;
quick_sort(nums, l, first);
quick_sort(nums, first + 1, r);
}
归并排序(Merge Sort)
void merge_sort(vector<int> &nums, int l, int r, vector<int> &temp)
{
if (l + 1 >= r)
{
return;
}
// divide
int m = l + (r - l) / 2;
merge_sort(nums, l, m, temp);
merge_sort(nums, m, r, temp);
// conquer
int p = l, q = m, i = l;
while (p < m || q < r)
{
if (q >= r || (p < m && nums[p] <= nums[q]))
{
temp[i++] = nums[p++];
}
else
{
temp[i++] = nums[q++];
}
}
for (i = l; i < r; ++i)
{
nums[i] = temp[i];
}
}
插入排序(Insertion Sort)
void insertion_sort(vector<int> &nums, int n)
{
for (int i = 0; i < n; ++i)
{
for (int j = i; j > 0 && nums[j] < nums[j-1]; --j)
{
swap(nums[j], nums[j-1]);
}
}
}
冒泡排序(Bubble Sort)
void bubble_sort(vector<int> &nums, int n)
{
bool swapped;
for (int i = 1; i < n; ++i)
{
swapped = false;
for (int j = 1; j < n - i + 1; ++j)
{
if (nums[j] < nums[j-1])
{
swap(nums[j], nums[j-1]);
swapped = true;
}
}
if (!swapped)
{
break;
}
}
}
选择排序(Selection Sort)
void selection_sort(vector<int> &nums, int n)
{
int mid;
for (int i = 0; i < n - 1; ++i)
{
mid = i;
for (int j = i + 1; j < n; ++j)
{
if (nums[j] < nums[mid])
{
mid = j;
}
}
swap(nums[mid], nums[i]);
}
}
以上排序代码调用方法为
void sort()
{
vector<int> nums = {1,3,5,7,2,6,4,8,9,2,8,7,6,0,3,5,9,4,1,0};
vector<int> temp(nums.size());
sort(nums.begin(), nums.end());
quick_sort(nums, 0, nums.size());
merge_sort(nums, 0, nums.size(), temp);
insertion_sort(nums, nums.size());
bubble_sort(nums, nums.size());
selection_sort(nums, nums.size());
}
快速选择
- Kth Largest Element in an Array
题目描述
在一个未排序的数组中,找到第 k 大的数字
输入输出样例
输入一个数组和一个目标值 k,输出第 k 大的数字。题目默认一定有解。
Input: [3,2,1,5,6,4] and k = 2
Output: 5
题解
快速选择一般用于求解 k-th Element 问题,可以在 O(n) 时间复杂度,O(1) 空间复杂度完成求解工作。快速选择的实现和快速排序相似,不过只需要找到第 k 大的枢(pivot)即可,不需要对其左右再进行排序。与快速排序一样,快速选择一般需要先打乱数组,否则最坏情况下时间复杂度为 O(n2),我们这里为了方便省略掉了打乱的步骤。
// 主函数
int findKthLargest(vector<int>& nums, int k)
{
int l = 0, r = nums.size() - 1, target = nums.size() - k;
while (l < r)
{
int mid = quickSelection(nums, l, r);
if (mid == target)
{
return nums[mid];
}
if (mid < target)
{
l = mid + 1;
}
else
{
r = mid - 1;
}
}
return nums[l];
}
// 辅函数 - 快速选择
int quickSelection(vector<int>& nums, int l, int r)
{
int i = l + 1, j = r;
while (true)
{
while (i < r && nums[i] <= nums[l])
{
++i;
}
while (l < j && nums[j] >= nums[l])
{
--j;
}
if (i >= j)
{
break;
}
swap(nums[i], nums[j]);
}
swap(nums[l], nums[j]);
return j;
}
桶排序
- Top K Frequent Elements (Medium)
题目描述
给定一个数组,求前 k 个最频繁的数字
输入输出样例
输入是一个数组和一个目标值 k。输出是一个长度为 k 的数组。
Input: nums = [1,1,1,1,2,2,3,4], k = 2
Output: [1,2]
在这个样例中,最频繁的两个数是 1 和 2。
题解
顾名思义,桶排序的意思是为每个值设立一个桶,桶内记录这个值出现的次数(或其它属性),然后对桶进行排序。针对样例来说,我们先通过桶排序得到三个桶 [1,2,3,4],它们的值分别为 [4,2,1,1],表示每个数字出现的次数。
紧接着,我们对桶的频次进行排序,前 k 大个桶即是前 k 个频繁的数。这里我们可以使用各种排序算法,甚至可以再进行一次桶排序,把每个旧桶根据频次放在不同的新桶内。针对样例来说,因为目前最大的频次是 4,我们建立 [1,2,3,4] 四个新桶,它们分别放入的旧桶为 [[3,4],[2],[],[1]],表示不同数字出现的频率。最后,我们从后往前遍历,直到找到 k 个旧桶。
vector<int> topKFrequent(vector<int>& nums, int k)
{
unordered_map<int, int> counts;
int max_count = 0;
for (const int & num : nums)
{
max_count = max(max_count, ++counts[num]);
}
vector<vector<int>> buckets(max_count + 1);
for (const auto & p : counts)
{
buckets[p.second].push_back(p.first);
}
vector<int> ans;
for (int i = max_count; i >= 0 && ans.size() < k; --i)
{
for (const int & num : buckets[i])
{
ans.push_back(num);
if (ans.size() == k)
{
break;
}
}
}
return ans;
}