3. 算法分析
3.1 评估算法效率
- 算法的计算复杂性
字母N表示问题规模,当N值变大时,N和算法运行时间之间的关系被称为该算法的计算复杂性(computational complexity)。
3.2 O标记
- O标记
计算机科学家用–种特殊记号表示算法的计算复杂性。这个符号为O标记(读作Big Oh)。
这个符号由一个大写的字母O及其后的一个用圆括号括起的公式组成,该公式表示运行时间随问题规模变化的函数。
字母O代表单词order(顺序),指的是近似值。
- 恒定时间
如果一个操作所需的时间与问题规模无关,则说该操作以恒定时间(constant time) 运行。
在O标记中,恒定时间用O(1)表示。O(1)的意思是当N变大时,程序的运行时间是常数,这是恒定时间操作的一个显著特征。
Dequeue的实现用下列for循环把该队列中每一项向数组头方向移一步:
for (i=1; i<queue->len; i++) {
queue->array[i-1] = queue->array[i];
}
如果队列包含N项,这个for循环就要执行N个周期。随着N的增加,for循环执行时间成正比例增加。
- 线性时间
如果一个操作的运行时间与问题规模成正比,则称此操作以线性时间(linear time)运行,用O标记表示为O(N)。
3.3 再看选择排序
如果给出一个有N个元素的数组,选择排序算法要访问每一个数组元素的位置,并确定该位置应该存放的值。
总的运行时间的公式可化简为:
N 2 + N 2 \frac {N^{2}+N}{2} 2N2+N?
当使用O标记来估计一个算法的计算复杂性时,目的是提供一种量化手段,以便衡量当N变大时,N的变化是如何影响算法的性能。
因为O标记并非一种精确的量化手段,所以我们最好能简化括号中的表达式,以便用最简单的形式量化算法的行为。
对圆括号里的公式应用下列步骤,可以简化O标记:
1)消去公式中任何随N变大而变得无足轻重的项。
2)消去任何常数系数。
用来表示选择排序的复杂性的表达式应为:
O
(
N
2
)
O(N2)
O(N2)
- 平方时间
运行性能为O(N2)表示的算法被称为以平方时间(quadratic time)运行。
3.4 分而治之策略
一旦发现怎样在一个层面上改善性能,就能用同样的算法递归地为每一个子数组排序。
- 分而治之算法
把一个问题分解成基本相等的子问题,并递归地解决每一个子问题, 这样的递归算法称为分而治之(divide-and-conquer)算法。
要确定分而治之方法是否适用于排序问题,来看一个有8个元素的数组的例子。
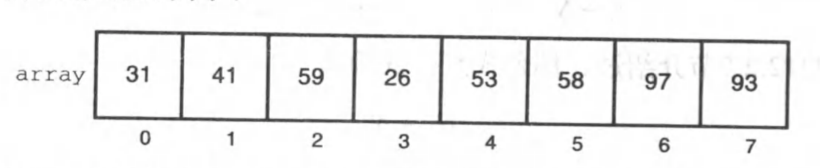

3.5 合并两个数组
- 合并
把已排序的子数组重组成一个完整数组,这种技术叫合并(merging)。
它基于一个事实,即完整的排序的第一个元素只能是arr1或arr2的第一个元素,但要取更小的那个元素作为第一个元素。
在这个例子中, 新数组中的第一个元素是arr1中的26。如果把这个元素放入array[0],实际上,就是把它从arr1中划掉,结果得到以下结构:
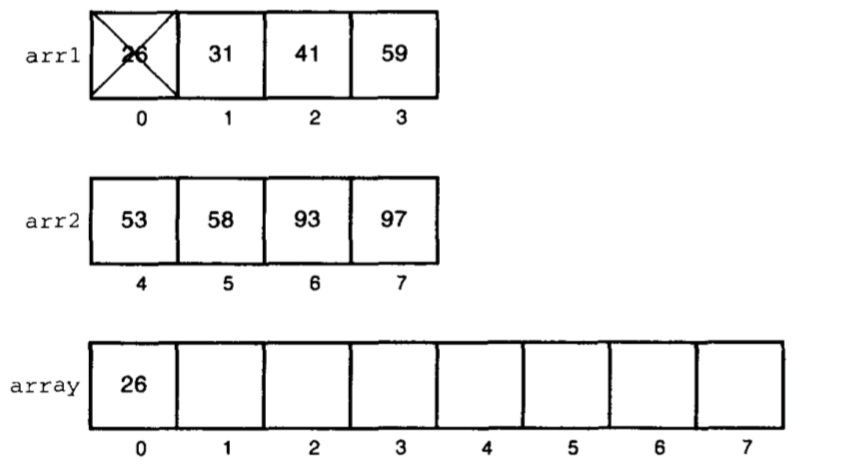
接着,下一个元素只能是两个子数组中第一个未用过的元素。把arr1中的31和arr2中的53比较,并选择前者:
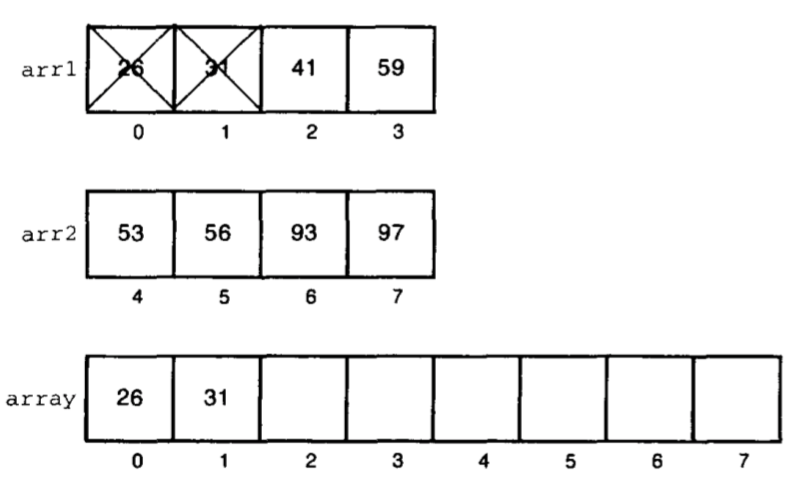
可以继续在arr1、arr2中选择较小值的过程,直到整个数组被填满为止。
3.6 合并排序算法
- 合并排序
合并操作与递归分解相结合,产生了一个新的排序算法——合并排序(mergesort)。
实现这个算法的方法如下:
函数SortIntegerArray首先判定数组的大小。如果数组没有元素或只有一个元素,那么数组必然已经被排过序。
如果数组包含的元素多于1个,就需要执行下列步骤。
1)把数组分成两个较小的子数组,每一个数组的大小是原数组的一半。
2) 递归调用Sort Integer Array为每一个小数组排序。
3) 合并两个小数组,写回原数组。
函数SortIntegerArray本身的代码如下:
void SortIntegerArray(int array[], int n) {
int i, n1, n2;
int *arr1, *arr2;
if (n>1) {
n1 = n/2;
n2 = n-n1;
arr1 = NewArray(n1, int);
arr2 = NewArray(n2, int);
for (i=0; i<n1; i++) {
arr1[i] = array[i];
}
for (i=0; i<n2; i++) {
arr2[i] = array[n1+i];
}
SortIntegerArray(arr1, n1);
SortIntegerArray(arr2, n2);
Merge(array, arr1, n1, arr2, n2);
FreeBlock(arr1);
FreeBlock(arr2);
}
}
在这个实现中,arr1和arr2是较小的数组,它们有效长度分别为n1和n2,所有困难的工作都由Merge完成。
Merge实现如下:
static void Merge(int array[], int arr1[], int n1, int arr2[], int n2) {
int p, p1, p2;
p = p1 = p2 = 0;
while (p1<n1 & p2<n2) {
if (arr1[p1]<arr2[p2]) {
array[p++]=arr1[p1++];
} else {
array[p++]=arr2[p2++];
}
}
while (p1<n1) array[p++]=arr1[p1++];
while (p2<n2) array[p++]=arr1[p2++];
}
Merge函数的参数有目标数组以及较小的数组arr1和arr2,还有它们的有效长度n1和n2。
下标p1和p2标志着每一个子数组的进度,p是array的下标。
在每一个循环周期中,函数从arr1或arr2中选择一个较小元素,把该值复制到array中。一旦任何一个子数组的元素用完,该函数就直接把另一个子数组中剩下的元素复制到目标数组中。
3.7 合并排序的计算复杂性
当调用合并排序的实现(SortIntegerArray函数)为N个数字排序时,运行时间可分成下面两部分:
-
在当前的递归分解层次上,执行操作所需的所有时间。
-
执行递归调用的时间。
在递归分解的最上面一层, 执行非递归操作所消耗的时间与N成正比。
任何一次SortIntegerArray调用的复杂性(如果不考虑其中的递归调用)需要O(N)次操作。
递归操作所需的总时间是递归分解的每一层所消耗的时间之和。总的来说,分解的结构如图17-3所示:
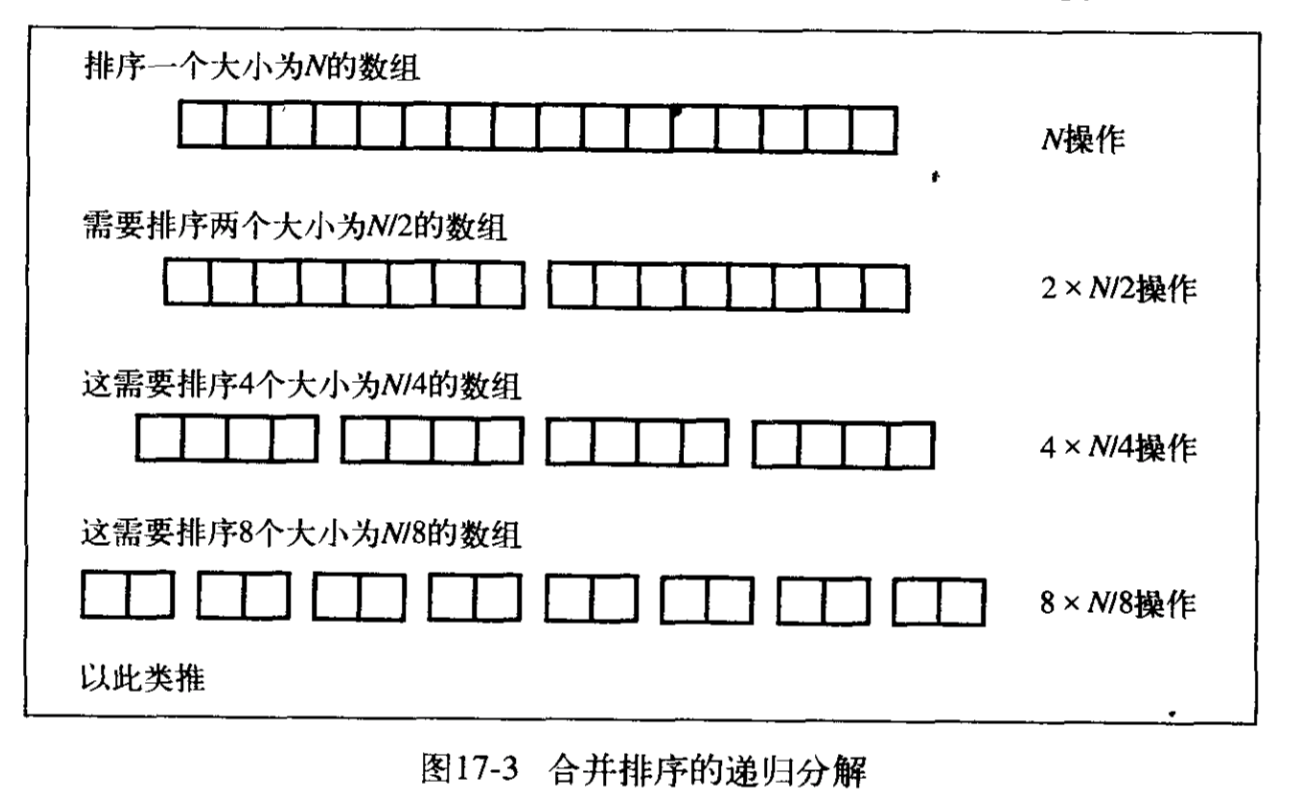
每一层的工作量总是和N直接成正比的。因此,确定工作总量就转化为确定层数的问题。
在递归层次结构的每一层中,N值都除以2。总层数等于在N=1之前将N除以2的次数。
用数学术语表述这个问题,就是说必须找到一个这样的k值,使得:
N
=
2
k
N=2^{k}
N=2k
得到k的值为:
k
=
l
o
g
2
N
k=log_2N
k=log2?N
因为层数为 k = l o g 2 N k=log_2N k=log2?N,且每一层的工作量与N成正比,所以总工作量与 N l o g 2 N Nlog_2N Nlog2?N成正比。
在计算机科学中,总是使用二进制对数(binary logarithm),即以2为底数的对数。
谈到计算复杂性的问题时,可以忽略对数的底数。这样,合并排序的计算复杂性可以写为:
O
(
N
l
o
g
N
)
O(NlogN)
O(NlogN)