[数据结构与算法]LeetCode Hot100 ---- 最长相关专题（动态规划）

动态规划解题步骤

核心思想是递推，难点在于想清楚 状态 dp[i] 代表什么，然后构造状态转移矩阵，利用初始条件递推出最终结果

1. 将原问题拆分成子问题
2. 确认状态
3. 确认边界状态（初始条件）
4. 状态转移方程

最长问题

647. 回文子串

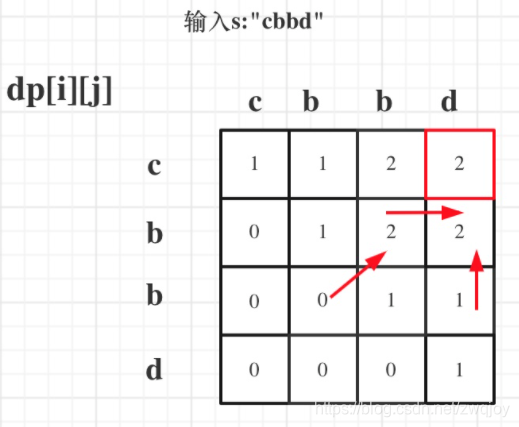
给定一个字符串，你的任务是计算这个字符串中有多少个回文子串。

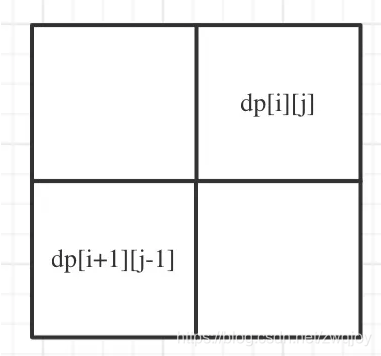
class Solution(object):
    def countSubstrings(self, s):
        """
        :type s: str
        :rtype: int
        """
        dp = [[False] * len(s) for _ in range(len(s))]
        result = 0

        for i in range(len(s) -1, -1, -1):
            for j in range(i, len(s)):
                if s[i] == s[j]:
                    if j - i <= 1:
                        result = result + 1
                        dp[i][j] = True
                    elif dp[i+1][j-1]:
                        result = result + 1
                        dp[i][j] = True
        return result

5. 最长回文子串

class Solution:
    def longestPalindrome(self, s: str) -> str:
        """
        :type s: str
        :rtype: int
        """
        dp = [[False] * len(s) for _ in range(len(s))]
        maxLength = 0
        left, right = 0, 0

        for i in range(len(s) -1, -1, -1):
            for j in range(i, len(s)):
                if s[i] == s[j]:
                    if j - i <= 1:
                        dp[i][j] = True
                    elif dp[i+1][j-1]:
                        dp[i][j] = True
                if dp[i][j] and j - i + 1 > maxLength:
                    left = i
                    right = j
                    maxLength = j - i + 1
        return s[left:right+1]

516. 最长回文子序列?

回文子串是要连续的，回文子序列可不是连续的！

class Solution(object):
    def longestPalindromeSubseq(self, s):
        """
        :type s: str
        :rtype: int
        """
        dp = [[0] * len(s) for _ in range(len(s))]
        for i in range(len(s)):
            dp[i][i] = 1
        for i in range(len(s)-1, -1, -1):
            for j in range(i+1, len(s)):
                if s[i] == s[j]:
                    dp[i][j] = dp[i+1][j-1] + 2
                else:
                    dp[i][j] = max(dp[i+1][j], dp[i][j-1])
        
        return dp[0][-1]

300. 最长递增子序列

?

class Solution(object):
    def lengthOfLIS(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """
        if not nums:
            return 0
        dp = [1] * len(nums)
        maxLength = 0
        for i in range(len(nums)):
            for j in range(i):
                if nums[i] > nums[j]:
                    dp[i] = max(dp[i], dp[j] + 1)
            if dp[i] > maxLength:
                maxLength = dp[i]
        return maxLength

674. 最长连续递增序列

class Solution(object):
    def findLengthOfLCIS(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """
        dp = [1] * len(nums)
        for i in range(len(nums)-1):
            if nums[i+1] > nums[i]:
                dp[i+1] = dp[i] + 1
        return max(dp) 

718. 最长重复子数组

给两个整数数组?A?和?B?，返回两个数组中公共的、长度最长的子数组的长度。

class Solution(object):
    def findLength(self, nums1, nums2):
        """
        :type nums1: List[int]
        :type nums2: List[int]
        :rtype: int
        """
        n, m = len(nums1), len(nums2)
        dp = [[0]* (m + 1) for _ in range(n + 1)]
        result = 0
        for i in range(1, n+1):
            for j in range(1, m+1):
                if nums1[i-1] == nums2[j -1]:
                    dp[i][j] = dp[i-1][j-1] + 1
                if dp[i][j] > result:
                    result = dp[i][j]
        return result

?1143. 最长公共子序列

本题和718. 最长重复子数组区别在于这里不要求是连续的了，但要有相对顺序，即："ace" 是 "abcde" 的子序列，但 "aec" 不是 "abcde" 的子序列。

class Solution(object):
    def longestCommonSubsequence(self, text1, text2):
        """
        :type text1: str
        :type text2: str
        :rtype: int
        """
        n, m = len(text1), len(text2)
        dp = [[0]* (m + 1) for _ in range(n + 1)]
        result = 0
        for i in range(1, n+1):
            for j in range(1, m+1):
                if text1[i-1] == text2[j -1]:
                    dp[i][j] = dp[i-1][j-1] + 1
                else:
                    dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])
                if dp[i][j] > result:
                    result = dp[i][j]
        return result

53. 最大子序和

class Solution(object):
    def maxSubArray(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """
        if len(nums) == 0:
            return 0
        dp = [0] * len(nums)
        dp[0] = nums[0]
        result = dp[0]
        for i in range(1, len(nums)):
            dp[i] = max(dp[i-1] + nums[i], nums[i])
            if dp[i] > result:
                result = dp[i]
        return result

128. 最长连续序列

给定一个未排序的整数数组 nums ，找出数字连续（不是升序是连续）的最长序列（不要求序列元素在原数组中连续）的长度。

class Solution:
    def longestConsecutive(self, nums: List[int]) -> int:
        length=len(nums)
        if length<2:
            return length
        nums.sort()
        dp=[0]*length
        dp[0]=1        
        for i in range(1, length):
            if nums[i]==nums[i-1]+1:
                dp[i]=dp[i-1]+1
            elif nums[i]==nums[i-1]:
                dp[i]=dp[i-1]
            else:
                dp[i]=1
        return max(dp)

最长连续公共字串

最长连续为1的字串

最长有效括号

最长无重复字符的连续字串

最长等差数列

最长上升连续序列

最长上升子序列

最长和谐子序列