[数据结构与算法]题解 [国家集训队]圈地计划

这篇题解主要是对建模的详细说明（？

众所周知，最小割求的是最小值，所以我们肯定要转化为理论最大值-实际最小值，先考虑一个 naive 的模型：

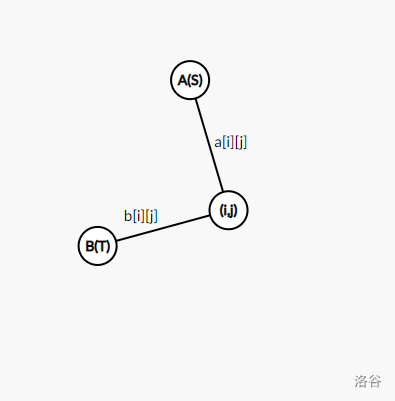
这种情况下，我们理想状态下 $(i,j)$ 的贡献应该是 $a_{i,j}+b_{i,j}$，很不幸，$(i,j)$ 只能取一种状态，也就是实际上它的贡献是 $a_{i,j}+b_{i,j}?\min (a_{i,j},b_{i,j})$。

这个时候明眼人已经能看出最小割了，回想一下最小割解决什么问题？集合划分的问题，建一个流网络，$s$ 为源点，$t$ 为汇点，每个节点 $(i,j)$ 连向 $s$，$t$，容量分别为 $a_{i,j},b_{i,j}$ ，一个 $s?t$ 割的实际意义就是与 $s$ 在同一子集的节点 $(i,j)$ 取 $a_{i,j}$，与 $t$ 在同一子集的节点 $(i,j)$ 取 $b_{i,j}$。最小割割掉的边，实际上就是每个节点舍弃的状态（舍弃最小，答案就最大）。

回到这个问题，看到网格图考虑黑白染色，对于黑点就按上述方式建模，对于白点就翻转一下源点和汇点就好。

但是，现在我们还是什么都没做，因为这个模型 P 用没有。真正让这个模型有用的就是 $c_{i,j}$ 的限制。

对于每一个黑点，由于我们的染色规则，必然它四个相邻的点是白点，考虑对于每个黑点计算贡献，显然这个东西可以拆开计算：

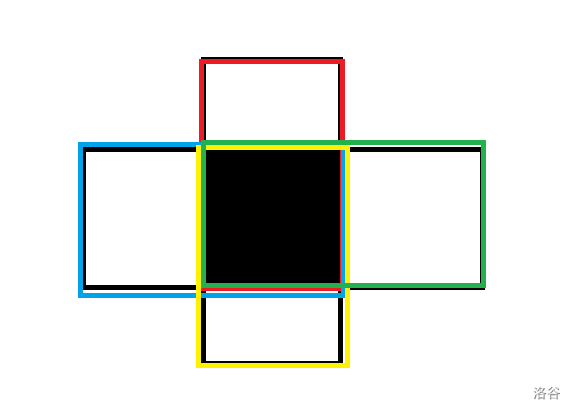
图很丑，见谅。

于是乎，一个黑点和四个白点理论最大贡献就是：

$\sum c_{i,j}+c_{i+dx,i+dy}(dx\in [?1,1],dy\in [?1,1])$

显然理论上限显然达不到，于是我们把刚刚的模型从垃圾桶捡回来（注意，这里是只有两个点的简单情况）：

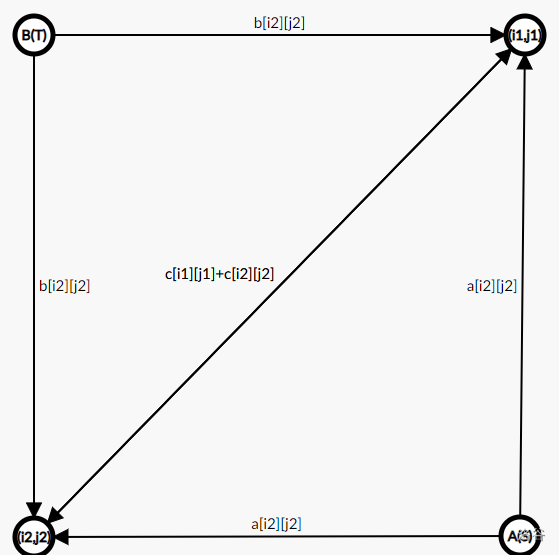
注意看中间是双向边。

问题解决了！

为什么呢？根据题目定义只有当两个相邻的点所取状态不同才会产生 $c$ 的贡献，此时也就是这两个点归属于同一集合（因为不同颜色的汇点源点正好相反），不用删去 $c_{i1,j1}+c_{i2,j2}$ 这条边，而如果两个点状态相同，它们会归属于不同集合，这样的情况下由于两者联通，$s,t$ 必然联通，不符合流网络中割的定义，就一定会删除 $c_{i1,j1}+c_{i2,j2}$ 这条边，也符合题意，所以跑个最大流求最小割就好了。