JZ59 按之字形顺序打印二叉树
(简单)
题目
描述
给定一个二叉树,返回该二叉树的之字形层序遍历,(第一层从左向右,下一层从右向左,一直这样交替)
例如:
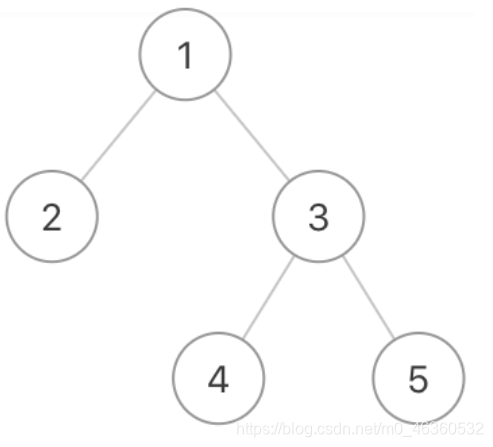
给定的二叉树是{1,2,3,#,#,4,5}
该二叉树之字形层序遍历的结果是
[
[1],
[3,2],
[4,5]
]
示例1
输入:
{1,2,3,#,#,4,5}
返回值:
[[1],[3,2],[4,5]]
示例2
输入:
{8,6,10,5,7,9,11}
返回值:
[[8],[10,6],[5,7,9,11]]
示例3
输入:
{1,2,3,4,5}
返回值:
[[1],[3,2],[4,5]]
思路
此题需要理解清楚的核心问题就是广度优先遍历和如果一次选定树结构的一层,BFS 我在前面的几道关于树的习题种已经用到了多次,而且之前也有写过相关文章,是基于图结构的:Java实现【邻接矩阵、邻接表的创建、遍历(DFS,BFS)】+图解+完整代码,因此树结构的 BFS 不再赘述,利用辅助队列就可以完成,而关于如何选定或者说间隔树结构对应队列中的层与层的结点,则可以每次在内层循环中记录下当前队列的当前长度,每次内层循环开始时,队列中存储的是本次要输出的此层的所有结点,而每次内层循环结束时,本层的所有结点已按相应顺序输出,队列中存储的是下一层的所有结点,想清楚了这个思路,这个问题便可以迎刃而解。
实现
在最后提交测试时,报了个错(如下图),那看来没有输入的话,题意就该按空二叉树来理解,因此也是要返回一个空数组的。
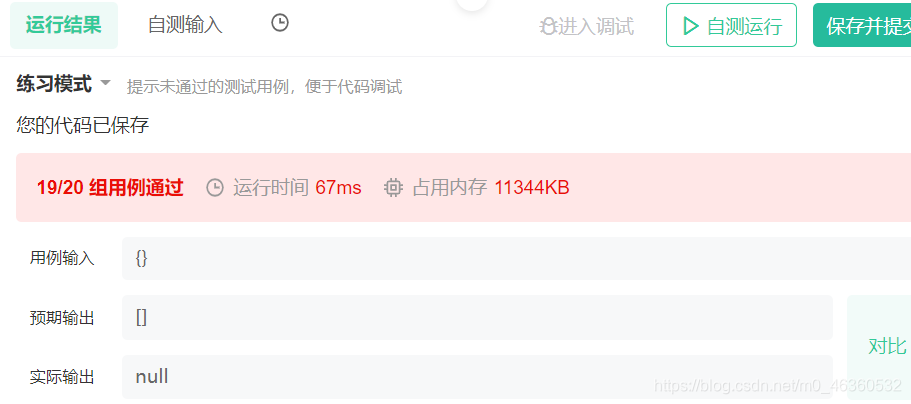
改一下就可以了
public class JZ59按之字形顺序打印二叉树 {
public ArrayList<ArrayList<Integer>> Print(TreeNode pRoot) {
ArrayList<ArrayList<Integer>> deepList = new ArrayList<>();
if (pRoot == null) {
return deepList;
}
Queue<TreeNode> queue = new LinkedList<>();
boolean flag = true;
queue.add(pRoot);
while (!queue.isEmpty()) {
int size = queue.size();
ArrayList<Integer> list = new ArrayList<>();
while (size > 0) {
TreeNode node = queue.poll();
if (flag) { //左-右
list.add(node.val);
} else { //右-左
list.add(0, node.val);
}
if (node.left != null) {
queue.add(node.left);
}
if (node.right != null) {
queue.add(node.right);
}
size--;
}
deepList.add(list);
flag = !flag;
}
return deepList;
}
}
不过。。。这效率怎么这么低,这是我有史以来在效率上最失败的一次了

那其他人都用的什么神仙方法??
我于是看了看官方的题解,这不跟我的代码一个思路吗,而且我测试了一下题解种其他人的代码,也和我的执行效率相似,甚至有些比我的还低,那看来不一定就是我的原因了,不知道是牛客后台统计的问题,还是其他原因。
JZ62 二叉搜索树的第k个结点
(简单)
题目
描述
给定一棵二叉搜索树,请找出其中的第k小的TreeNode结点。
示例
输入:
{5,3,7,2,4,6,8},3
返回值:
4
说明:
按结点数值大小顺序第三小结点的值为4
思路
刚看到这个题时,我第一反应是想到了堆排序,此题如果用堆排序的思想去做,那么首先还得将这个二叉树的结点转为数组后,再去用堆排序处理,并加上第 k 小的终止条件,即构建小根堆,用小根堆的堆顶交换 k 次对应的尾元素即可,但是当我想到将这个二叉树的结点转为数组这一点后,我立马就打消了用堆排序算法进行实现的念头,因为既然已经需要遍历一遍二叉树了,那么为什么不在遍历的同时,将各结点按其值的大小顺序,插入到一个数组或链表中呢,最后直接返回第 k 个结点元素不就可以了,于是,我写下了下面这种实现。
实现
public class JZ62二叉搜索树的第k个结点 {
List<TreeNode> list = new ArrayList<TreeNode>();
TreeNode KthNode(TreeNode pRoot, int k) {
if (pRoot == null || k <= 0) { //另外,k值过大的情况在下面判断,这样就可以利用 list 中的结点数
return null;
}
//遍历,遍历的同时按从小到大顺序插入到结点链表中
preTraverse(pRoot);
if (k > list.size()) {
return null;
}
return list.get(k - 1);
}
/**
* 按从小到达的顺序插入结点
* @param node
*/
public void orderAdd(TreeNode node) {
int i = 0;
while (i < list.size() && node.val > list.get(i).val) {
i++;
}
list.add(i, node);
}
public void preTraverse(TreeNode pRoot) {
if (pRoot == null) {
return;
}
orderAdd(pRoot);
preTraverse(pRoot.left);
preTraverse(pRoot.right);
}
}