剑指 Offer 10- I：斐波那契数列

关于为什么需要动态规划，还要从经典的斐波那契数列说起（力扣https://leetcode-cn.com/problems/fei-bo-na-qi-shu-lie-lcof/）

递归

这种题当然难不倒我，大一C语言就教了好吗？

class Solution {

    /**
     * @param Integer $n
     * @return Integer
     */
    function fib($n) {
        if($n<=1){
            return $n;
        }
        return $this->fib($n-1)+$this->fib($n-2);
    }
}

在测试用例$n=39时，超出运行时间限制了...

本例中的递归解法差在哪了（只是本例，不是所有递归一概而论的）

如图：它有大量的重复计算，算f(n)前需要先算f(n-1)、f(n-2)，再依次向下算...

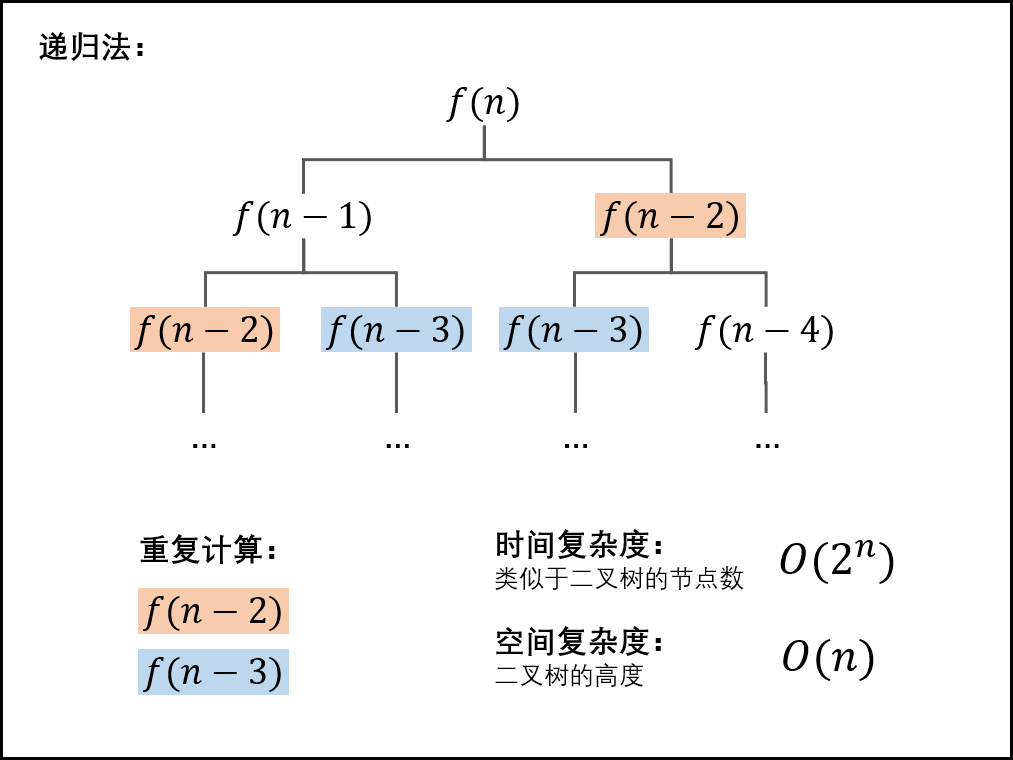
?map图

有一些改良的方法，就是在缓存或者增加数组来存储f(0)、f(1)...f(n-2)这些值，以避免重复计算，虽然会额外增加内存空间，但是思路还是不错的

class Solution {

	public static $map = [];
    /**
     * @param Integer $n
     * @return Integer
     */
    function fib($n) {
    	if($n<=1){
    		self::$map[$n] = $n;
    		return $n;
    	}else{
    		$a = isset(self::$map[$n-1]) ? self::$map[$n-1] : $this->fib($n-1);
    		$b = isset(self::$map[$n-2]) ? self::$map[$n-2] : $this->fib($n-2);
    		self::$map[$n] = ($a+$b)%1000000007;
    		return self::$map[$n];
    	}
    }
}

因为$map随着元素增加而线性递增，空间复杂度o(n)，还可以

动态规划

动态规划和递归有一点相似，但是动态规划往往要求总结和显式指出规律，在处理具有重叠子问题时相对递归的优势就非常明显。

f(n)只跟f(n-1)和f(n-2)有关，那么可以只记录更新f(n-1)、f(n-2)

class Solution {

    /**
     * @param Integer $n
     * @return Integer
     */
    function fib($n) {
    	if($n<=1){
    		return $n;
    	}
    	$a = 0;
    	$b = 1;
    	for($i=2;$i<=$n;$i++){
    		$sum = ($a+$b)%1000000007;
    		$a = $b;
    		$b = $sum;
    	}
    	return $sum;
    }
}

剑指 Offer 10- II. 青蛙跳台阶问题

与斐波那契数列几乎相同的还有青蛙跳台问题

https://leetcode-cn.com/problems/qing-wa-tiao-tai-jie-wen-ti-lcof/

递归

function findRepeatNumber($nums) {
	$arr = [];
	for($i=0;$i<count($nums);$i++){
		if(! in_array($nums[$i], $arr)){
			$arr[] = $nums[$i];
		}else{
			return $nums[$i];
		}
	}
	return [];
}

气不气~?

map

存一下过往数据

class Solution {

	public static $map=[];
    /**
     * @param Integer $n
     * @return Integer
     */
	function numWays($n) {
	    if($n<=1){
	    	self::$map[$n]=1;
			return 1;
		}else{
			$a = isset(self::$map[$n-1]) ? self::$map[$n-1] : $this->numWays($n-1);
    		$b = isset(self::$map[$n-2]) ? self::$map[$n-2] : $this->numWays($n-2);
			self::$map[$n]=($a + $b)%1000000007;
			return self::$map[$n];
		}
	}
}

100%夸张了吧...

动态规划

class Solution {

    /**
     * @param Integer $n
     * @return Integer
     */
    function numWays($n) {
    	if($n<=1){
    		return 1;
    	}
    	$a = $b = 1;
    	for($i=2;$i<=$n;$i++){
    		$sum = ($a+$b)%1000000007;
    		$a = $b;
    		$b = $sum;
    	}
    	return $sum;
    }
}