[数据结构与算法]B树 B+树和红黑树详解

1. 树

1.1 2-3树

? 为了保证二叉查找树的平衡性，允许树中的一个节点保存多 个键。

1.1.1 2-3树的定义

一棵2-3查找树要么为空树，要么满足如下两个条件;

• 2-节点：

  含有一个键和两条链，左链指向的2-3树中的键都小于该节点，右链指向的2-3树中的键都大于该节点

• 3-节点：

  含有两个键和三条链，左链指向的2-3树中的键都小于该节点，中链指向的2-3树中的键都位于该节点的两个键之间，右链指向的2-3树中的键都大于该节点

1.1.2 查找

? 将二叉查找树的查找算法一般化，可以得到2-3查找树的查找算法。判断一个键是否在树中，先在根节点查找是否命中。若命中，则查找结束；若未命中，则根据比较结果找到对应的区间连接，并在连接指向的子树中继续执行查找算法（递归）。如果这个连接为NULL，则查找失败。

1.1.3 插入

1.1.3.1 向2-结点中插入新键

? 先进行查找，后将键放到未找到的节点上。插入后仍然保证树的平衡状态。如果查找后未找到的节点是一个2-节点，则只需要将新的元素放到这个2-节点里面使其变成一个3-节点即可。

1.1.3.2 向一棵只含有一个3-结点的树插入新键

? 假设2-3树中只含有一个3-节点，这个节点有两个键，没有空间来插入第三个键。则假设这个节点能存放三个元素，使其暂时成为一个4-节点。将这个4-节点中间的键进行提升，左边的键成为其左子树，右边的键成为其右子树。插入完成后，变回2-3树，树的高度从0到1；

1.1.3.3 向一个父节点为2-结点的3-结点中插入新值

? 先将节点插入3-节点，使其临时成为一个4-节点。把4-节点的中间元素提升到父节点（2-节点）中。把剩余的键分别挂到父节点恰当的位置。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-spD9mQLh-1627393422343)(resource/1619077308948.png)]

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-S3qZ6wzO-1627393422348)(resource/1619077329619.png)]

1.1.3.4 向一个父节点为3-结点的3-结点中插入新键

? 当插入节点是一个3-节点的时候，将该节点进行拆分，中间元素提升到父节点。由于父节点也是一个3-节点，故父节点也进行拆分，将中间元素向上提升。直到遇到一个2-节点，将其变成一个3-节点后，插入完成。

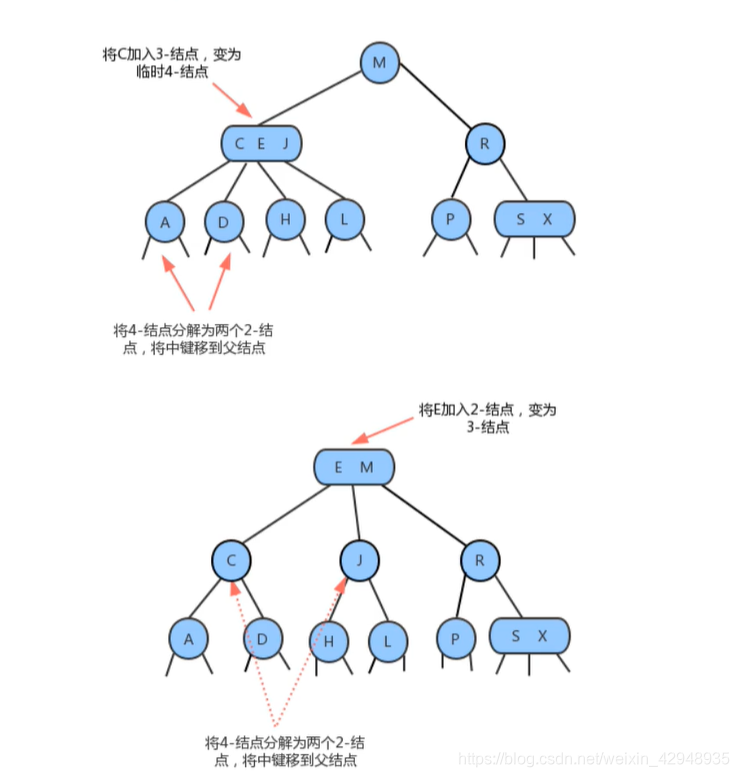
1.1.3.5 分解根节点

? 当插入节点到根节点的路径上全部都是3-节点的时候，最终根节点会变成一个临时的4-节点。此时，需要将根节点拆分成两个2-节点，中间的键向上提升成为根节点（2-节点）

1.1.4 2-3树的性质

一棵完全平衡的2-3树具有以下性质：

1. 任意空链接到根节点的路径长度相等
2. 只有当根节点变成临时的4-节点并分解根节点后，树的高度才会+1
3. 普通的二叉查找树是自顶向上生长的，而2-3树是自底向上生长的

1.1.5 2-3树的实现

直接实现2-3树比较复杂，因为：

• 需要处理不同的节点类型，非常复杂
• 需要多次比较操作来将节点下移
• 需要上移来拆分4-节点
• 拆分4-节点的情况有很多种

2-3查找树实现起来比较复杂，在某些情况插入后的平衡操作可能会使得效率降低。但是2-3查找树作为一种比较重要的概念和思路，对于理解红黑树、B树B+树非常重要。

1.2 红黑树

红黑树是2-3树思想的简单实现。其基本思想是用标准的二叉查找树（全是2-节点）和一些额外的信息（替换3-节点）来表示2-3树。树中的链接分为两种类型：

• 红链接：将两个2-节点连接起来构成一个3-节点
• 黑链接：2-3树中的普通链接

将3-节点表示为由一个左斜的红色链接相连的两个2-节点。其优点是：可以直接使用标准的二叉查找树的get方法。

1.2.1 红黑树的定义

含有红黑链接并满足以下条件的二叉查找树：

1. 红链接均为左链接；
2. 没有任何一个节点同时和两个红链接相连；
3. 任意空链接到根节点的路径上的黑链接数量相同

2-3树与红黑树的对应关系：

1.2.2 红黑树节点API

? 每个节点都只会有一条指向自己的链接，可以在节点中添加一个布尔类型的变量color来表示链接的颜色。如果指向它的链接是红色的，变量值为true；如果是黑色的，变量值为false。

package com.zipeng.tree.redblacktree;

/**
 * @author: zipeng Li
 * 2021/4/22  16:35
 *
 * 红黑树节点
 */
public class Node<K,V> {
    /**
     * 左子节点
     */
    public Node left;
    /**
     * 右子节点
     */
    public Node right;
    /**
     * 存储键
     */
    public K key;
    /**
     * 存储值
     */
    public V value;
    /**
     * 父节点指向该节点的链接的颜色
     * true -> 红色
     * false -> 黑色
     */
    public boolean color;

    public Node(Node left, Node right, K key, V value, boolean color) {
        this.left = left;
        this.right = right;
        this.key = key;
        this.value = value;
        this.color = color;
    }

    public Node() {
    }
}

1.2.3 红黑树的平衡化

? 对红黑树进行一些增删改查的操作后，可能会出现红色的右链接或者两条连续红色的链接，而这些都不满足红黑树的定义，所以我们需要对这些情况通过旋转进行修复，让红黑树保持平衡。

1.2.3.1 左旋

条件：当某个节点的左子节点为黑色，右子节点为红色，此时需要左旋

假设：当前节点为h，其右子节点为x；

左旋过程：

1. 让x的左子节点变为h的右子节点：h.right = x.left；
2. 让h成为x的左子节点：x.left = h;
3. 让h的color属性变为x的color属性值：x.color = h.color;
4. 让h的color属性变为red: h.colo = true;

1.2.3.2 右旋

条件：某个节点的左子节点是红色，且左子节点的左子节点也是红色，则需要右旋

假设：当前节点为n，左子节点为x

右旋过程：

1. 让x的右子节点成为h的左子节点：h.left = x.right;
2. 让h成为x的右子节点：x.right = h;
3. 让x的color变为h的color：x.color = h.color;
4. 让h的color变为red

1.2.4 向单个2-节点插入新键

一棵只含有一个键的红黑树只含有一个2-节点，插入另一个键后，需要进行旋转。

• 如果新键小于当前节点的键，只需新增一个红色节点即可，新的红黑树和单个3-节点完全等价

• 如果新键大于当前节点的键，则新增的红色节点会产生一条红色的右链接。此时需要左旋把红色右链变成左链，插入完成。形成的新红黑树依然和3-节点等价，其中含有两个键，一条红色的链接。

1.2.5 向底部的2-节点插入新键

? 新建一个红链接节点和对应底部节点连接，根据插入情况，调用上述对应的调整方法进行调整

1.2.6 颜色反转

? 当一个节点的左右子节点都是red时，只需把左右子节点变为black，同时让当前节点的颜色变成red即可。

1.2.7 向一棵双键树（即一个3-节点）中插入新键

? 有三种情况：

• 新建大于两个键–>直接进行颜色反转

  

• 新建小于两个键–>先右旋，后颜色反转

• 新建介于两键之间–>先左旋，后右旋，再颜色反转

1.2.8 根节点的颜色总是黑色

? 由于根节点不存在父节点，所有每次插入操作后，都需要把根节点的颜色设置为黑色。

1.2.9 向树底部的3-节点插入新键

? 假设在树的底部的一个3-节点下加入一个新的节点。

1.3 B树

• B-tree 树即 B 树，B 即 Balanced，平衡的意思。有人把 B-tree 翻译成 B-树，容易让人产生误解。会以为 B-树是一种树，而 B 树又是另一种树。实际上，B-tree 就是指的 B 树。
• 前面已经介绍了 2-3 树和 2-3-4 树，他们就是 B 树，这里我们再做一个说明，我们在学习 Mysql 时，经常听到说某种类型的索引是基于 B 树或者 B+树的，如图:

对上图的说明：

• B 树的阶：节点的最多子节点个数。比如 2-3 树的阶是 3，2-3-4 树的阶是 4
• B-树的搜索，从根结点开始，对结点内的关键字（有序）序列进行二分查找，如果命中则结束，否则进入查询关键字所属范围的儿子结点；重复，直到所对应的儿子指针为空，或已经是叶子结点
• 关键字集合分布在整颗树中, 即叶子节点和非叶子节点都存放数据.
• 搜索有可能在非叶子结点结束
• 其搜索性能等价于在关键字全集内做一次二分查找

1.4 B + 树

B+树是 B 树的变体，也是一种多路搜索树。

对上图说明：

• B+树的搜索与 B 树也基本相同，区别是 B+树只有达到叶子结点才命中（B 树可以在非叶子结点命中），其性能也等价于在关键字全集做一次二分查找
• 所有关键字都出现在叶子结点的链表中（即数据只能在叶子节点【也叫稠密索引】），且链表中的关键字(数据)恰好是有序的。
• 不可能在非叶子结点命中
• 非叶子结点相当于是叶子结点的索引（稀疏索引），叶子结点相当于是存储（关键字）数据的数据层
• 更适合文件索引系统
• B 树和 B+树各有自己的应用场景，不能说 B+树完全比 B 树好，反之亦然