一、概念
由训练数据构建一组基分类器(base classifier),将每个基分类器的预测结果进行组合(ensemble)得到最终结果。
为什么组合分类器的效果好于基分类器?
设基分类器的误差为 ? \epsilon ?,对 N N N个组合分类器来说,只有超过一半以上基分类器都预测错误时,最终预测结果才错误。当基分类器互相独立时,组合分类器的错误率为
∑ i = N 2 N C N i ? i ( 1 ? ? ) N ? i \sum_{i=\frac{N}{2}}^NC_N^i\epsilon^i(1-\epsilon)^{N-i} ∑i=2N?N?CNi??i(1??)N?i
当 ? < 0.5 \epsilon<0.5 ?<0.5时, e n s e m b l e ensemble ensemble的错误率更小。
因此当基分类器之间相关性不强;且基分类器分类误差小于0.5时,组合分类器的分类效果好于基分类器。
二、构建方法
如何在原始数据上构建多个分类器?
1. 对训练样本进行再抽样
对原始训练样本再抽样得到多个训练集,在每个训练集上训练一个分类器。
抽样方法:
- bagging(bootstrap aggregating)
基分类器是并行产生训练的。
从数据集中随机有放回抽样N次,得到大小为N的训练集。每次抽样每个样本被抽到的概率为 1 ? ( 1 ? 1 N ) N 1-(1-\frac{1}{N})^N 1?(1?N1?)N 趋近于 1 ? 1 / e = 0.632 1-1/e = 0.632 1?1/e=0.632,故每次抽样得到的训练集大小为63.2%,验证集大小为36.8%。
重复抽样k次,最终通过基分类器结果的多数表决得到最终结果。
- boosting
基分类器是迭代产生训练的。
不同于bagging的随机抽样,boosting每一轮训练结束后会调整样本的权值,增加分类错误样本的权值,减少分类正确样本的权值,根据权值进行下一轮抽样和模型学习。
三、模型实例
1. Adaboost
对第 j j j个分类器:
- j = 0 j=0 j=0时样本初始权值为 1 / N 1/N 1/N
- 计算基分类器的加权分类错误率 ? = ∑ i = 1 N ω i I ( y ^ i ≠ y i ) \epsilon = \sum_{i=1}^N\omega_iI(\hat y_i≠y_i) ?=∑i=1N?ωi?I(y^?i??=yi?)
- 若 ? > 0.5 \epsilon>0.5 ?>0.5则恢复所有样本权值为 1 / N 1/N 1/N,重新抽样。
- 确定基分类器的重要性: α = 1 2 l n ( 1 ? ? ? ) \alpha = \frac{1}{2}ln(\frac{1-\epsilon}{\epsilon}) α=21?ln(?1???)。 ? < 0.5 \epsilon<0.5 ?<0.5 时 α > 0 \alpha>0 α>0; ? > 0.5 \epsilon>0.5 ?>0.5 时 α < 0 \alpha<0 α<0
- 更新样本权值:分类正确的样本 ω ′ = ω Z × e ? α \omega' = \frac{\omega}{Z}×e^{-\alpha} ω′=Zω?×e?α;分类错误的样本 ω ′ = ω Z × e α \omega' = \frac{\omega}{Z}×e^{\alpha} ω′=Zω?×eα
- 最终预测结果为 s i g n ( ∑ j = 1 K α j y ^ j ) sign(\sum_{j=1}^K\alpha_j\hat y_j) sign(∑j=1K?αj?y^?j?)
优点:训练误差呈指数递减
e e n s e m b l e ≤ ∏ [ ? i ( 1 ? ? i ) ] ≤ ∏ [ 1 ? 4 γ i 2 ] ≤ e x p ( ? 2 ∑ γ i 2 ) e_{ensemble} ≤ \prod[\sqrt {\epsilon_i(1-\epsilon_i)}] ≤ \prod[\sqrt{1-4\gamma_i^2}]≤exp(-2\sum \gamma_i^2) eensemble?≤∏[?i?(1??i?)?]≤∏[1?4γi2??]≤exp(?2∑γi2?)
γ j = 0.5 ? ? j \gamma_j = 0.5 - \epsilon_j γj?=0.5??j?。表示第 j j j个分类器比随机猜测强多少。
缺点:倾向于分类错误的样本,容易过拟合。
2. GBDT
前期知识:加法模型与前向分步算法。
K个基分类器的组合,有
f ( x ) = ∑ k = 1 K β k C k ( x ; γ k ) f(x) = \sum_{k=1}^K\beta_kC_k(x; \gamma_k) f(x)=∑k=1K?βk?Ck?(x;γk?)
N个样本,最终最小化损失函数即为
m i n ∑ i = 1 N L ( y i , ∑ k = 1 K β k C k ( x ; γ k ) ) min\sum_{i=1}^NL(y_i, \sum_{k=1}^K\beta_kC_k(x; \gamma_k)) min∑i=1N?L(yi?,∑k=1K?βk?Ck?(x;γk?))
优化思路为从前往后每次只优化一个基分类器。即
f 0 ( x ) = 0 f_0(x) = 0 f0?(x)=0
对 k = 0 , 1 , 2... K k = 0, 1, 2...K k=0,1,2...K:
a r g m i n ∑ i = 1 N L ( y i , f k ? 1 ( x ) + β k C k ( x ; γ k ) ) argmin\sum_{i=1}^NL(y_i, f_{k-1}(x)+\beta_kC_k(x; \gamma_k)) argmin∑i=1N?L(yi?,fk?1?(x)+βk?Ck?(x;γk?))
得到参数并更新,最终分类器为 f K ( x ) f_K(x) fK?(x)
Adaboost算法即为前向分布加法算法,其中损失函数为指数损失函数 L ( y , f ( x ) ) = e x p [ ? y f ( x ) ] L(y, f(x))=exp[-yf(x)] L(y,f(x))=exp[?yf(x)]
前期知识:梯度下降 Gredient Decent
梯度是函数增加最快的地方。梯度下降法即为沿函数的负梯度方向前进,从而最快找到最低点。
对于 f ( θ ) f(\theta) f(θ),寻找 θ \theta θ使函数值最小。初始化 θ 0 \theta_0 θ0?,则 θ 1 = θ 0 ? α Δ θ 0 f ( θ ) \theta_1 = \theta_0-\alpha \Delta_{\theta_0}f(\theta) θ1?=θ0??αΔθ0??f(θ),不断迭代。
GBDT 梯度提升树
基分类器:决策树
f M ( x ) = ∑ m = 1 M T m ( x ; θ m ) f_M(x) = \sum_{m=1}^MT_m(x;\theta_m) fM?(x)=∑m=1M?Tm?(x;θm?)
在构造过程中,根据前向加法模型,第 m m m步优化为
a r g m i n θ m ∑ i = 1 N L ( y i , f m ? 1 ( x i ) + T m ( x i ; θ m ) ) \mathop{argmin}\limits_{\theta_m}\sum_{i=1}^N L(y_i, f_{m-1}(x_i)+T_m(x_i;\theta_m)) θm?argmin?∑i=1N?L(yi?,fm?1?(xi?)+Tm?(xi?;θm?))
若损失函数为平方损失,则回归树的boosting可转化为拟合残差
a
r
g
m
i
n
θ
m
∑
i
=
1
N
L
(
y
i
,
f
m
?
1
(
x
i
)
+
T
m
(
x
i
,
θ
m
)
)
\mathop{argmin}\limits_{\theta_m}\sum_{i=1}^N L(y_i, f_{m-1}(x_i)+T_m(x_i,\theta_m))
θm?argmin?∑i=1N?L(yi?,fm?1?(xi?)+Tm?(xi?,θm?))
=
a
r
g
m
i
n
θ
m
∑
i
=
1
N
(
y
i
?
f
m
?
1
(
x
i
)
?
T
m
(
x
i
;
θ
m
)
)
2
= \mathop{argmin}\limits_{\theta_m}\sum_{i=1}^N(y_i-f_{m-1}(x_i)-T_m(x_i;\theta_m))^2
=θm?argmin?∑i=1N?(yi??fm?1?(xi?)?Tm?(xi?;θm?))2
求导可得 = a r g m i n θ m ∑ 2 ( y i ? f m ? 1 ( x i ) ? T m ( x i ; θ m ) ) = \mathop{argmin}\limits_{\theta_m}\sum 2(y_i-f_{m-1}(x_i)-T_m(x_i;\theta_m)) =θm?argmin?∑2(yi??fm?1?(xi?)?Tm?(xi?;θm?))
y i ? f m ? 1 ( x i ) ? T m ( x i ; θ m ) = r i ? T m ( x i ; θ m ) y_i-f_{m-1}(x_i)-T_m(x_i;\theta_m) = r_i-T_m(x_i;\theta_m) yi??fm?1?(xi?)?Tm?(xi?;θm?)=ri??Tm?(xi?;θm?)
即第m步需要用 T m ( x ; θ m ) T_m(x;\theta_m) Tm?(x;θm?) 拟合残差 r r r
若损失函数为指数损失,则为Adaboost算法
对于复杂的损失函数,利用梯度下降法的近似方法GBDT进行优化
将 f ( x ) f(x) f(x)参数化,相当于找到一个 f ( x ) f(x) f(x),使 ∑ i = 1 N L ( y i , f ( x i ) ) \sum_{i=1}^N L(y_i, f(x_i)) ∑i=1N?L(yi?,f(xi?))最小
由梯度下降,迭代更新 f ( x i ) f(x_i) f(xi?)
f ( x i ) : = f ( x i ) ? Δ f m ? 1 ( x i ) L ( y i , f ( x i ) ) f(x_i) := f(x_i)-\Delta_{f_{m-1}(x_i)}L(y_i,f(x_i)) f(xi?):=f(xi?)?Δfm?1?(xi?)?L(yi?,f(xi?))
又因为 f m ( x i ) = f m ? 1 ( x i ) + h m ( x i ) f_m(x_i) = f_{m-1}(x_i)+h_m(x_i) fm?(xi?)=fm?1?(xi?)+hm?(xi?)
所以相当于每次用 h m ( x i ) h_m(x_i) hm?(xi?)拟合 ? Δ f m ? 1 ( x i ) L ( y i , f ( x i ) ) -\Delta_{f_{m-1}(x_i)}L(y_i,f(x_i)) ?Δfm?1?(xi?)?L(yi?,f(xi?))
即计算负梯度作为残差样本进行训练。
GBDT用于分类
GBDT
3. 随机森林
随机森林对决策树进行bagging,同时每次选择不同的特征来构建基分类器。
树的相关性越低,每棵树的误差越小,RF的泛化误差越小。因此要尽可能随机化,减少决策树之间的相关性。
Forest-RI
不考察全部特征,而是每次随机选择F个特征来构造树。每棵树完全增长不进行修剪。最终使用多数表决法对结果进行组合。
F F F越大,树的强度越高,树之间的相关性越大。作为折中,通常取 F = l o g 2 d + 1 F=log_2d+1 F=log2?d+1
Forest-RC
如果特征数量少,很难保证树的独立性,可以加大特征空间,创建新特征。在结点处,新特征通过随机选择 L L L个输入特征进行线性组合来创造,线性系数为区间 [ ? 1 , 1 ] [-1,1] [?1,1]的均匀分布。
三、组合方法的特征
-
模型的方差和偏差:模型简单,用不同训练样本得到的分类器基本相同,方差很小,但是偏差很大。
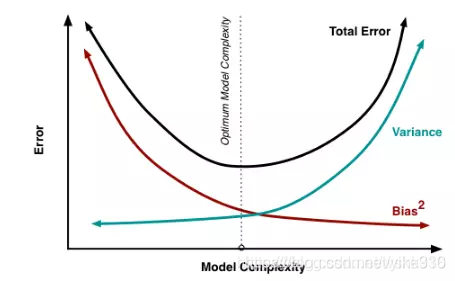
-
Boosting主要关注降低偏差,因此Boosting能基于泛化性能相当弱的学习器构建出很强的集成,比如深度很浅的决策树。
-
Bagging主要关注降低方差,因此它需要选择偏差较小的基分类器,如在不剪枝的决策树、神经网络等学习器上效用更为明显。
为什么GBDT使用CARET作为基分类器?
- 决策树可以认为是if-then规则的集合,易于理解,可解释性强,预测速度快。
- 决策树算法相比于其他的算法需要更少的特征工程,比如可以不用做特征标准化,可以很好的处理字段缺失的数据,也可以不用关心特征间是否相互依赖等。决策树能够自动组合多个特征,它可以毫无压力地处理特征间的交互关系并且是非参数化的,因此你不必担心异常值或者数据是否线性可分(举个例子,决策树能轻松处理好类别A在某个特征维度x的末端,类别B在中间,然后类别A又出现在特征维度x前端的情况)。
- 单独使用决策树算法时,有容易过拟合缺点。所幸的是,通过各种方法,抑制决策树的复杂性,降低单颗决策树的拟合能力,再通过梯度提升的方法集成多个决策树,最终能够很好的解决过拟合的问题。由此可见,梯度提升方法和决策树学习算法可以互相取长补短,是一对完美的搭档。至于抑制单颗决策树的复杂度的方法有很多,比如限制树的最大深度、限制叶子节点的最少样本数量、限制节点分裂时的最少样本数量、吸收bagging的思想对训练样本采样(subsample),在学习单颗决策树时只使用一部分训练样本、借鉴随机森林的思路在学习单颗决策树时只采样一部分特征、在目标函数中添加正则项惩罚复杂的树结构等。