[数据结构与算法]排序算法之归并排序

排序算法之归并排序

算法思维

归并排序（Merge sort）是建立在归并操作上的一种有效的排序算法。该算法是采用分治法的一个非常典型的应用。该算法采用经典的分治策略（分治法将问题分成一些小的问题然后递归求解，而治的阶段则将分的阶段得到的各答案"修补"在一起，即分而治之)。
作为一种典型的分而治之思想的算法应用，归并排序的实现由两种方法：
1.自上而下的递归（所有递归的方法都可以用迭代重写，所以就有了第 2 种方法）；
2.自下而上的迭代；

算法步骤

1.申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列；

2.设定两个指针，最初位置分别为两个已经排序序列的起始位置；

3.比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置；

4.重复步骤 3 直到某一指针达到序列尾；

5.将另一序列剩下的所有元素直接复制到合并序列尾。

算法图解

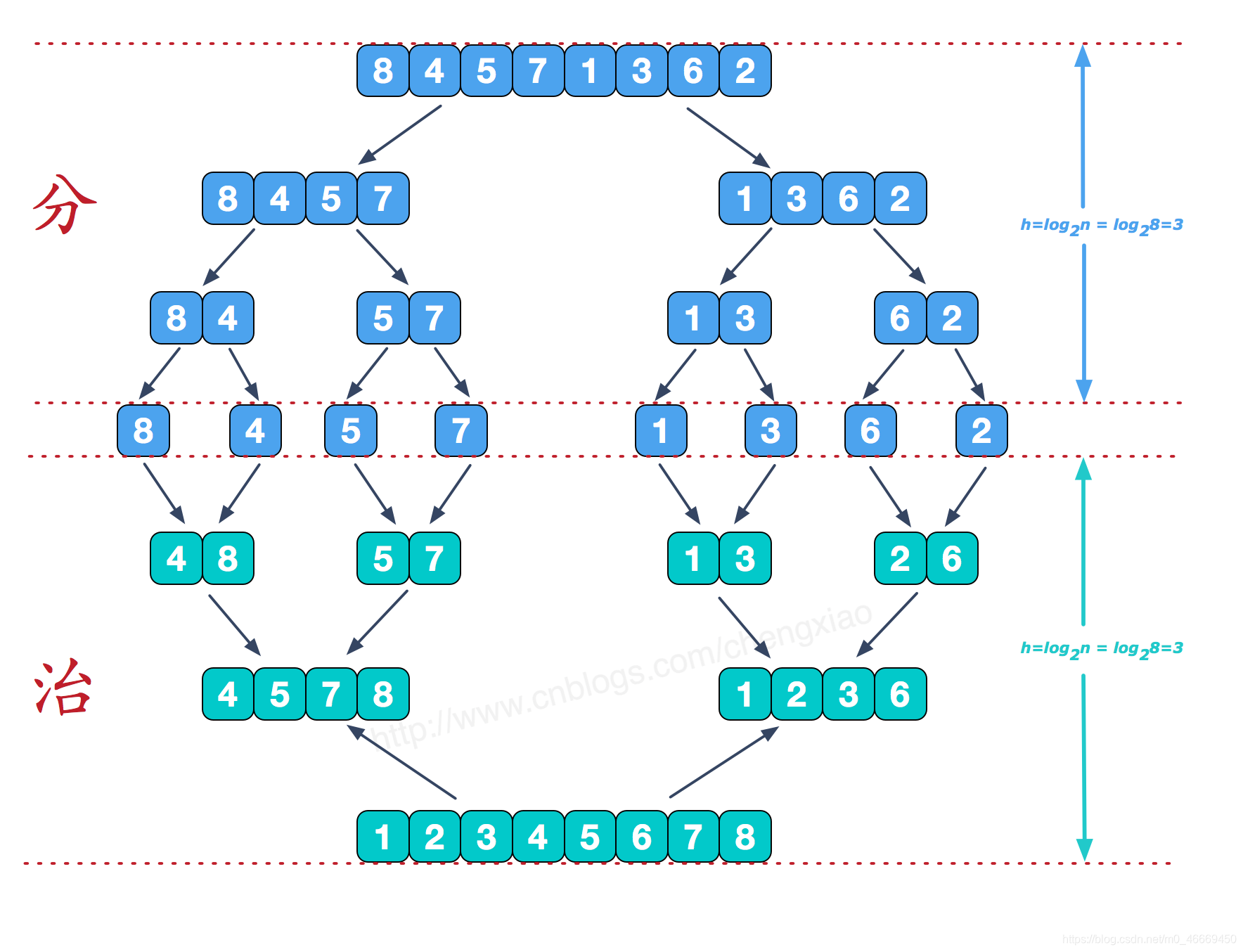
我们需要将两个已经有序的子序列合并成一个有序序列，比如上图中的最后一次合并，要将[4,5,7,8]和[1,2,3,6]两个已经有序的子序列，合并为最终序列[1,2,3,4,5,6,7,8]，来看下实现步骤。

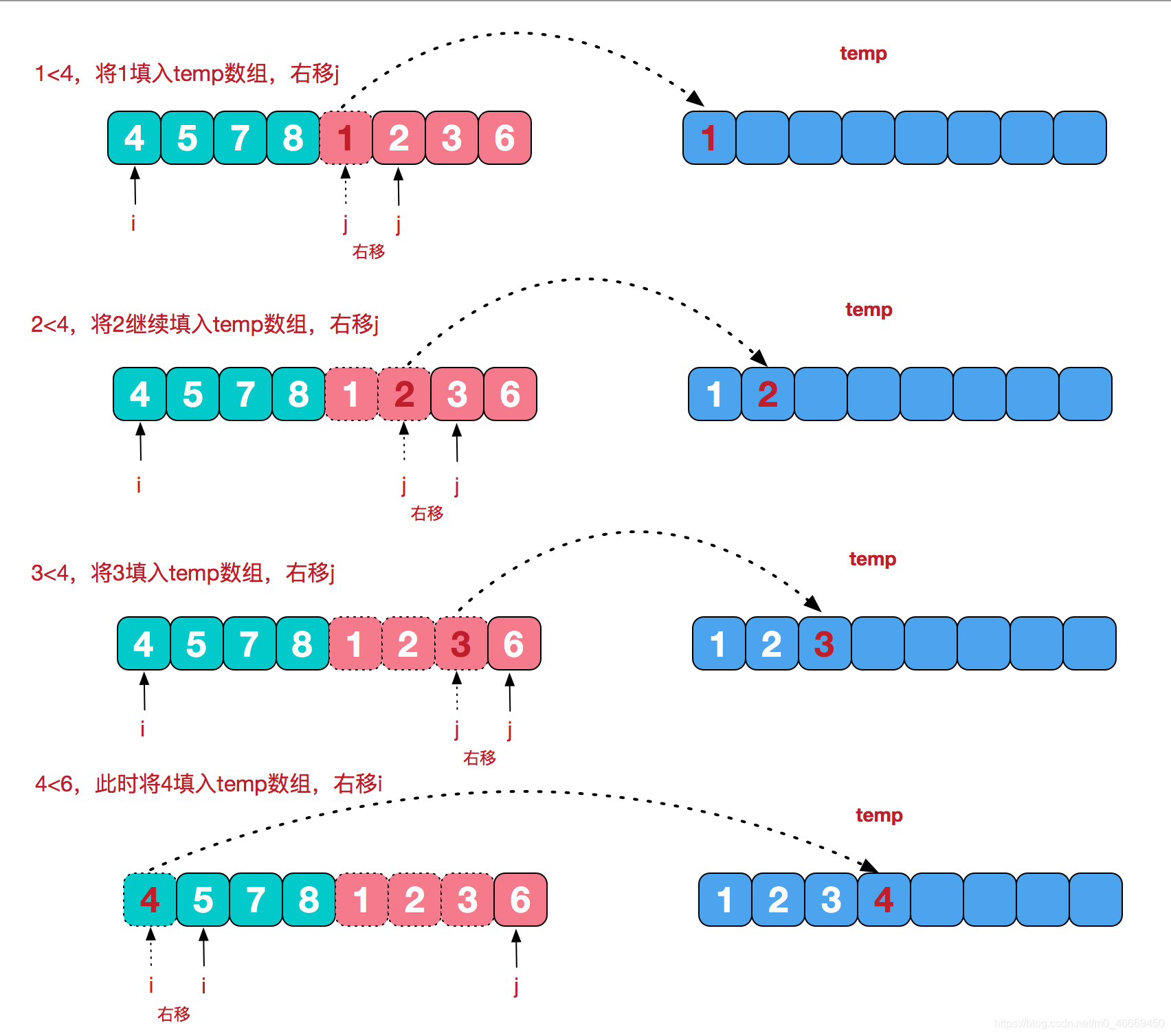
代码模板

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int m_sort[N],arr[N];
void merge_sort(int l,int r,int a[])
{
    int mid=(l+r)>>1;
    if(l>=r) return;
    else
    {
        merge_sort(l,mid,a);   //左边归并排序，使得左子序列有序
        merge_sort(mid+1,r,a); //右边归并排序，使得右子序列有序
    }
    int i=l;  //左序列指针
    int j=mid+1; //右序列指针
    int t=0; //临时数组指针
    while(i<=mid&&j<=r)
    {
        if(a[i]>a[j]) m_sort[t++]=a[j++];
        else m_sort[t++]=a[i++];
    }
    while(i<=mid) m_sort[t++]=a[i++];  //将左边剩余元素填充进m_sort中
    while(j<=r) m_sort[t++]=a[j++];   //将右边剩余元素填充进m_sort中
    int k=0;
    while(l<=r) a[l++]=m_sort[k++];   //将m_sort中的元素全部拷贝到原数组中
}
int main()
{
    int n;
    cin>>n;
    for(int i=0;i<n;i++) cin>>arr[i];
    merge_sort(0,n-1,arr);
    for(int i=0;i<n;i++) cout<<arr[i]<<' ';
    cout<<endl;
    return 0;
}

如果觉得写的不错点个赞吧 ^ - ^