Priority Queues
1 API和初级实现 API and elementary implementations





//泛型<>,中间是类名,表示声明的MinPQ实例只能储存Transaction类型的值
//MinPQ类:删除最小值
MinPQ<Transaction> pq = new MinPQ<Transaction>();
while (StdIn.hasNextLine()){
String line = StdIn.readLine();
Transaction item = new Transaction(line); //readline自动读取下一行,可见源码
pq.insert(item);
if (pq.size()>M){
pq.delMin();
}
}
- 如果M和N很大,elementary PQ所需时间会很长
- 如果用二叉堆数据结构,时间和空间复杂度俱佳,最接近最优解
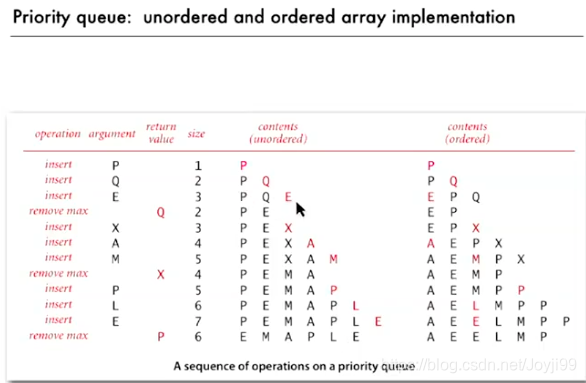
- 内容无序需要每次遍历所有元素来寻找最大
- 内容有序,每次需要把大的元素移动一位来插入小的元素,好处在于移除最小项更容易
- 无序数组优先队列的实现:
package Chapter02;
import edu.princeton.cs.algs4.*;
import java.security.Key;
import static com.sun.xml.internal.xsom.impl.UName.comparator;
public class UnorderedMaxPQ<Key extends Comparable<Key>> {
private Key[] pq; //pq[i] = ith element on pq
private int N; //number of elements on pq
public UnorderedMaxPQ(int capacity){ //没有创建泛型数组
pq = (Key[]) new Comparable[capacity];
}
public boolean isEmpty(){
return N == 0;
}
public void insert(Key x){
pq[N++] = x; //输入下一个数据,插入到最末
}
public Key delMax(){
int max = 0;
for (int i = 1; i < N; i++) {
if (less(max,i)) max = i;
}
exch(max,N-1);
return pq[--N];//删除最后一行
}
private void exch(int i, int j) {
Key swap = pq[i];
pq[i] = pq[j];
pq[j] = swap;
}
private boolean less(int i, int j) {
if (comparator == null) {
return ((Comparable<Key>) pq[i]).compareTo(pq[j]) < 0;
}
else {
return comparator.compare(pq[i], pq[j]) < 0;
}
}
}

2 二叉堆 binary heaps
2.1 堆的定义
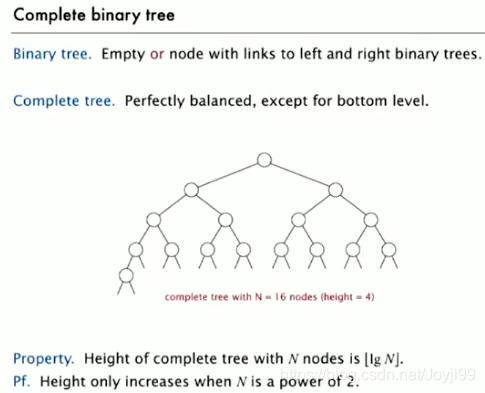
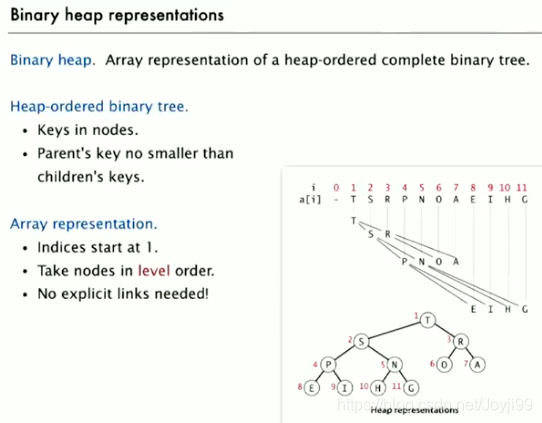
- 二叉树的每个结点都大于等于它的两个子节点时,它被称为堆有序
- 二叉堆是一组能够用堆有序的完全二叉树排序的元素,并在数组中按照层级储存(不使用数组的第一个位置)
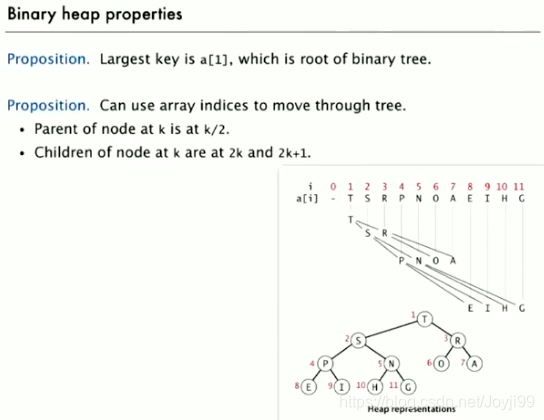
- 在一个堆中,位置k的结点的父结点的位置为k/2,而它的两个子结点的位置分别为2k和2k+1
2.2 堆的算法
2.2.1 由下至上的堆有序化
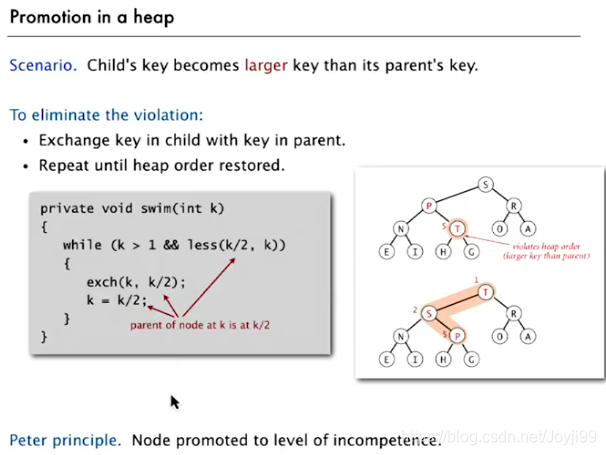
public class MaxPQ<Key extends Comparable<Key>> {
private Key[] pq; //基于堆的完全二叉树
//堆有序化:上浮
private void swim(int k){
while (k > 1 && less(k/2,k)){
exch(k/2,k);
k = k/2; //迭代,继续检查上一个结点
}
}
private boolean less(int i,int j){
return pq[i].compareTo(pq[j]) < 0;
}
private void exch(int i,int j){
Key t = pq[i];
pq[i] = pq[j];
pq[j] = t;
}
}
插入元素
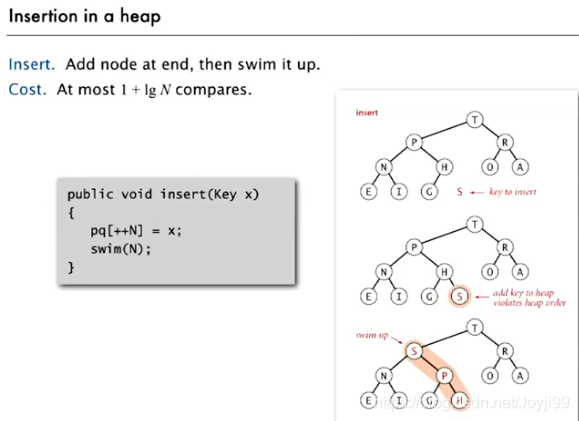
package Chapter02;
public class MaxPQ<Key extends Comparable<Key>> {
private Key[] pq; //基于堆的完全二叉树
private int N = 0;//存储于pq[1...N]中,pq[0]没有使用
public MaxPQ(int maxN){
pq = (Key[]) new Comparable[maxN + 1];
}
public boolean isEmpty(){
return N == 0;
}
public int size(){
return N;
}
//堆有序化:上浮
private void swim(int k){
while (k > 1 && less(k/2,k)){
exch(k/2,k);
k = k/2; //迭代,继续检查上一个结点
}
}
//插入元素
public void insert(Key x){
pq[++N] = x;
swim(N);
}
private boolean less(int i,int j){
return pq[i].compareTo(pq[j]) < 0;
}
private void exch(int i,int j){
Key t = pq[i];
pq[i] = pq[j];
pq[j] = t;
}
}
2.2.2 由上至下的堆有序化

package Chapter02;
public class MaxPQ<Key extends Comparable<Key>> {
private Key[] pq; //基于堆的完全二叉树
private int N = 0;//存储于pq[1...N]中,pq[0]没有使用
public MaxPQ(int maxN){
pq = (Key[]) new Comparable[maxN + 1];
}
public boolean isEmpty(){
return N == 0;
}
public int size(){
return N;
}
//堆有序化:下沉
private void sink(int k){
while (2*k <= N){
int j = 2*k;
if (j < N && less(j,j+1)) j++;
if (!less(k,j)) break;
exch(k,j);
k = j;
}
}
private boolean less(int i,int j){
return pq[i].compareTo(pq[j]) < 0;
}
private void exch(int i,int j){
Key t = pq[i];
pq[i] = pq[j];
pq[j] = t;
}
}
删除最大元素
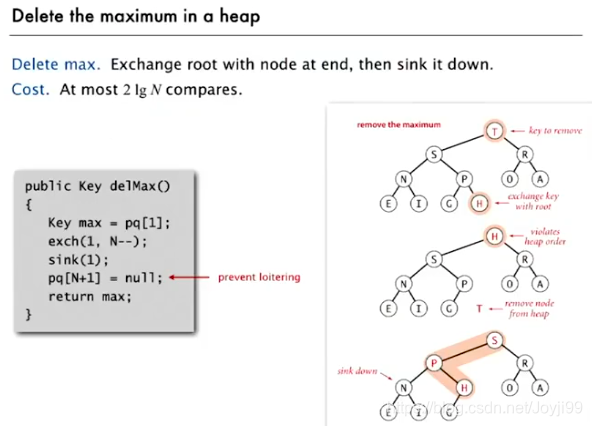
package Chapter02;
public class MaxPQ<Key extends Comparable<Key>> {
private Key[] pq; //基于堆的完全二叉树
private int N = 0;//存储于pq[1...N]中,pq[0]没有使用
public MaxPQ(int maxN){
pq = (Key[]) new Comparable[maxN + 1];
}
public boolean isEmpty(){
return N == 0;
}
public int size(){
return N;
}
//堆有序化:下沉
private void sink(int k){
while (2*k <= N){
int j = 2*k;
if (j < N && less(j,j+1)) j++;
if (!less(k,j)) break;
exch(k,j);
k = j;
}
}
//删除最大元素
public Key delMax(){
Key max = pq[1];
exch(1,N--);//1先和N交换,然后N变为N-1
sink(1);
pq[N+1] = null;//不在使用的元素设为null,以便系统回收它所占的空间
return max;
}
private boolean less(int i,int j){
return pq[i].compareTo(pq[j]) < 0;
}
private void exch(int i,int j){
Key t = pq[i];
pq[i] = pq[j];
pq[j] = t;
}
}
- 基于堆的优先队列

- 有逻辑的四部分
package Chapter02;
public class MaxPQ<Key extends Comparable<Key>> {
private Key[] pq; //基于堆的完全二叉树
private int N;//存储于pq[1...N]中,pq[0]没有使用 size
public MaxPQ(int capacity){
pq = (Key[]) new Comparable[capacity + 1]; //因为不用pq[0],所以capacity要+1
}
public boolean isEmpty(){
return N == 0;
}
public int size(){
return N;
}
//堆有序化:上浮
private void swim(int k){
while (k > 1 && less(k/2,k)){
exch(k/2,k);
k = k/2; //迭代,继续检查上一个结点
}
}
//插入元素
public void insert(Key x){
pq[++N] = x;
swim(N);
}
//堆有序化:下沉
private void sink(int k){
while (2*k <= N){
int j = 2*k;
if (j < N && less(j,j+1)) j++;
if (!less(k,j)) break;
exch(k,j);
k = j;
}
}
//删除最大元素
public Key delMax(){
Key max = pq[1];
exch(1,N--);//1先和N交换,然后N变为N-1
sink(1);
pq[N+1] = null;//不在使用的元素设为null,以便系统回收它所占的空间
return max;
}
private boolean less(int i,int j){
return pq[i].compareTo(pq[j]) < 0;
}
private void exch(int i,int j){
Key t = pq[i];
pq[i] = pq[j];
pq[j] = t;
}
}
2.3 复杂度


- unferflow & overflow下溢和溢出

- 优先队列的数据类型需要immutable,如果用户可以改变值,无法保证堆排序操作是正常的

3 堆排序 heapsort
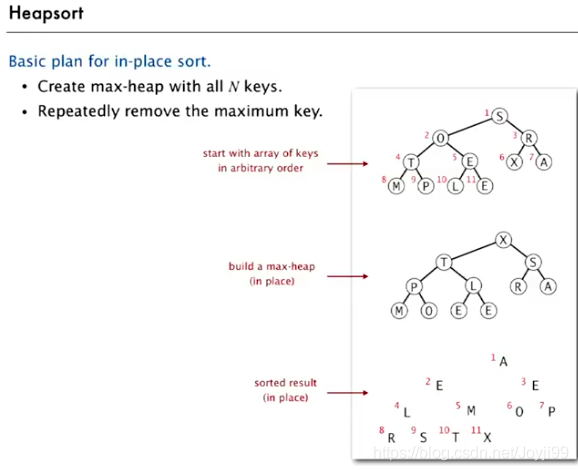
3.1 堆的构造
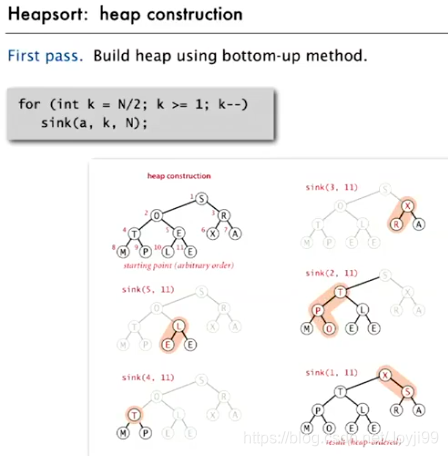
3.2 下沉排序

package Chapter02;
public class Heap {
public static void sort(Comparable[] pq){
int N = pq.length;
//堆的构造
for (int k = N/2; k >= 1 ; k--) {
sink(pq,k,N);
}
//下沉排序
while (N>1){
exch(pq,1,N--);//pq[1]和最后一项交换后,N-1,最后一项不再属于pq
sink(pq,1,N);//此时的N是-1后的N
}
}
private static void sink(Comparable[] pq, int k, int N){
while (2*k <= N){
int j = 2*k;
if (j < N && less(pq,j,j+1)) j++;
if (!less(pq,k,j)) break;
exch(pq,k,j);
k = j;
}
}
private static boolean less(Comparable[] pq, int i, int j){
return pq[i-1].compareTo(pq[j-1]) < 0;//堆的pq[i]是array的pq[i-1],因为数组从0开始
}
private static void exch(Comparable[] pq, int i, int j){
Comparable t = pq[i-1];
pq[i-1] = pq[j-1];
pq[j-1] = t;//考虑到pq[0]存在,处理同上
}
// print array to standard output
private static void show(Comparable[] a) {
for (int i = 0; i < a.length; i++) {
StdOut.println(a[i]);
}
}
public static void main(String[] args) {
String[] a = StdIn.readAllStrings();
sort(a);
show(a);
}
}

3.3 mathematical analysis

- cache memory高速缓冲存储器
3.4 所有排序算法总结
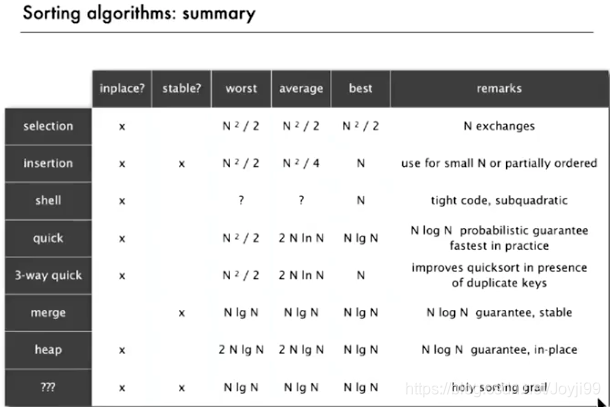
4 应用:事件驱动模拟 event-driven simulation
- 一群在正方形中随意碰撞的粒子,可能互相碰撞,也可能碰到墙


package Chapter02;
import edu.princeton.cs.algs4.StdDraw;
public class BouncingBalls {
public static void main(String[] args) {
int N = Integer.parseInt(args[0]);
Ball[] balls = new Ball[N];
for (int i = 0; i < N; i++) {
balls[i] = new Ball();
}
while (true){
StdDraw.clear();
for (int i = 0; i < N; i++) {
balls[i].move(0.5);
balls[i].draw();
}
StdDraw.show(50);
}
}
}
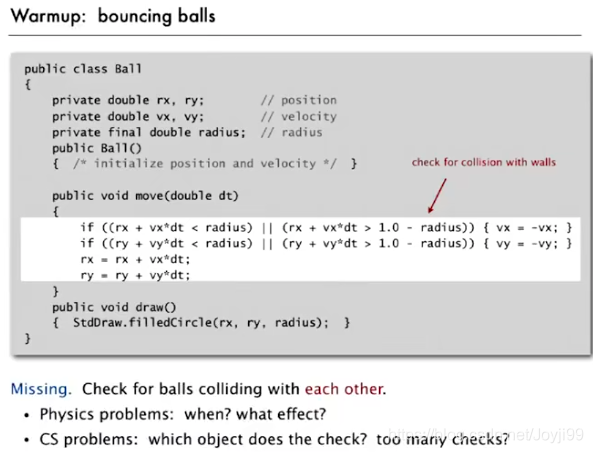
package Chapter02;
import edu.princeton.cs.algs4.StdDraw;
public class Ball {
private double rx, ry; //position
private double vx, vy; //velocity
private final double radius = 0.1; //radius
public Ball(){}
public void move(double dt){
//check for collision with walls
if ((rx + vx*dt < radius) || (rx + vx*dt > 1.0 - radius)){//wall at x=1
vx = -vx;
}
if ((ry + vy*dt < radius) || (ry + vy*dt > 1.0 - radius)){
vy = -vy;
}
rx = rx + vx*dt;
ry = ry + vy*dt;
}
public void draw(){
StdDraw.filledCircle(rx,ry,radius);
}
}

- 以量子大小的dt离散时间








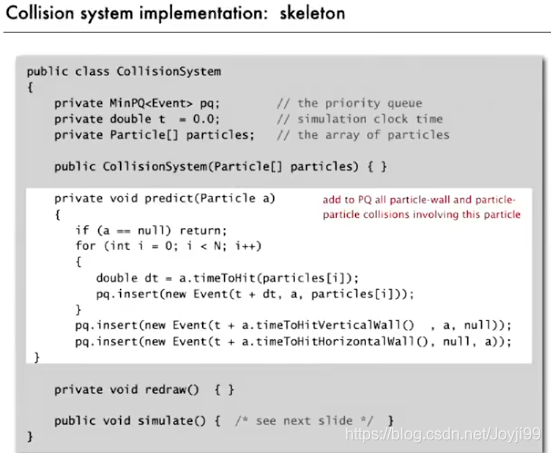

- 源码见alsg4 --> CollisionSystem
% java CollisionSystem
% java CollisionSystem < billards.txt
% java CollisionSystem < brownian.txt
% java CollisionSystem < diffusion.txt