0/1背包(一)暴力枚举与贪心算法
简单0/1背包问题概述:
(大致是这么个意思,杜撰自老师ppt,hhhh)
假定你因缘分进入一个藏宝地宫,里面奇珍异宝n件(n当然大得你数不过来)。你当然想尽可能多地带走珍宝,无奈你只有一个背包,且该背包只可承重c千克。超出此重量背包就会裂开(也就是说无法带走超出重量的物品)。地宫里的每件珍宝都有重量wi和价值vi。请问,如何挑选珍宝才能使你背出的珍宝价值最大?当然是在背包不裂开的情况下。
一个具体实例:
假定珍宝一共有5件,其重量(用符号W表示)与价值(用符号V表示),i为各个物品得下标,如下表所示:
| i | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Vi (单位$) | 60 | 100 | 120 | 30 | 40 |
| Wi(单位kg) | 10 | 20 | 30 | 10 | 20 |
| Vi/Wi | 6 | 5 | 4 | 3 | 2 |
你的背包的总承重为50kg;问:怎么装东西才能得到最大价值;
(该实例是一个简单例子,我们可以一眼看出,最优解为物品2与物品3装入背包,获得价值为220$,这也是该问题的最优解,记下该解)
暴力枚举算法:
针对上述简单实例,我们之所以可以一眼看出问题的答案,是因为我们针对小规模问题,采取了暴力枚举算法,简而言之,由于问题规模不大,所以我们可以在可观时间内获得0/1背包的最优解。
此时,我们把所有可能的序列都列一遍,由于0/1背包主要讨论的问题是放与不放的问题,即该物品非0即1,因此从理论上来讲,这是一个排列组合问题,时间复杂度大概如下公式所示:
暴力枚举的代码:
#include <iostream>
#include<stdio.h>
#include<algorithm>
#include<cmath>
#include<string.h>
#define num_proj 5
using namespace std;
//按照需要输入宝物数量
int value[num_proj]={60,100,120,30,40};
int weight[num_proj]={10,20,30,10,20};
int bagage = 50;
//宝物的定义
int solution[num_proj];//中间方案
int final_solu[num_proj];//最终解决方案
int max_value=0;//最大价值
void get_bin_num(int num){
memset(solution,0,num_proj);
int i = 5;
int bin = num;
while(bin > 0){
i--;
solution[i]=bin % 2;
bin = ceil(bin /2);
}
}
//简单的十进制转二进制的函数,
//利用二进制来决定哪一个装,哪一个不装
/*
例如 31:
二进制为 1 1 1 1 1
这个就说明是所有物品1,2,3,4,5都装进去
*/
int main(){
int loop_num = 1<<num_proj;
//获得全部的数字,得到2^num_proj
while(loop_num>=0){
//遍历所有可能情况
loop_num--;
get_bin_num(loop_num);
int cur_weight = 0;
int cur_value = 0;
for(int i =0;i<5;i++){
if (solution[i]==1){
cur_weight += weight[i];
cur_value += value[i];
}
}
if(cur_value > max_value && cur_weight <= bagage){
/*cout<<cur_value<<" "<<cur_weight<<" "<<max_value<<endl;
比较获得最大值,如果满足条件:
1最大值比当前最大值大;
2当前重量小于等于背包承重;
则记录下解决办法,更新最大值。
*/
for(int j = 0;j<num_proj;j++){
final_solu[j] = solution[j];
}
max_value = cur_value;
}
}
cout<<"solution is : "<<endl;
for(int j = 0;j<num_proj;j++){
cout << final_solu[j]<<" ";
}
}
结果示意
但是如果不是5件物品呢,万一你掉进了很牛很牛的宝藏库,宝物的件数远远超出你能数数解决的范围(大致为10e5)呢?指数的时间复杂度很可能会把你一生的时间全部耗尽,因此,我们需要一些启发式算法来帮你做出决定。
贪心算法:
针对上述问题,最直观,快速且有效的(不一定最优)解决方法必定是贪心算法。
1. 贪心算法介绍:
贪心算法,是一种贪婪的算法,顾名思义,也就是挑选眼前所有的选择中最优的一个选择,直到算法结束。
只要每一步都选择局部最优解,那么累加起来的结果必定是全局最优解的一个近似解。(注:只能是近似解,而不是绝对最优解,后面会有例子方便理解,话说这个性质也和人生一样,有时候总是选择最好的,人生反而会过的不太顺利,扯远了扯远了)
2. 0/1背包贪心算法的解决思路:
针对0/1背包问题,我们把自己代入,解决该问题可以大体有一定的思路:
(1)将眼前的宝物排序;
(2)根据排序的结果按优选择带出的物品;
该思路下,贪心算法解决0/1背包最精华的部分,也就是如何解决物品的排序问题。(排序,排序,排序重要的问题说3遍)
3. 0/1背包问题的排序方式:
想要解决排序问题,我们首先得拎清楚,排序的对象有哪些,即可以按照物品的哪些属性进行排序
(1)按照物品的本身存在的价值(假设用符号V表示)进行排序;
(2)按照物品的重量(假设用符号W表示)进行排序;
(3)按照物品的价值密度(价值/重量,即V/W)的比值进行排序;
三种排序方式中,前两种方法存在明显的短板。
对于方法一,如果价值高的物品重量也重,那么很有可能最后求得的解离最优解相去甚远,也许只能捡一个价值最高的物品,而其他物品加起来的价值要远远高于单一物品;
对于方法二,如果价值低的物品恰好重量也很轻,那么你很有可能最后捡了一堆没人要的垃圾。
而第三种排序方式相较于前两种,有明显的优势,由于背包能背的重量(假设用符号C表示)一定,所以每次都选择价值密度最大的物品,这样一来最后在理想情况下获得的收益一定是最大的,为:
最优价值密度 * 重量;
(注:最优价值密度不是指某一个具体的价值密度,而是一种理想化简化)
第三种排序思路,也是简单0/1背包中最常用得思路,是精髓所在;
贪心代码:
#include <iostream>
#include<stdio.h>
#include<algorithm>
#include<cmath>
#include<string.h>
#define num_proj 5
using namespace std;
//按照需要输入宝物数量
struct treasure{
int no;//物品序号
double value;//物品价值
double weight;//物品重量
double per_value;
};
treasure project[num_proj];
double value[num_proj]={60,100,120,30,40};
double weight[num_proj]={10,20,30,10,20};
int baggage = 50;
//预设价值
int solution[num_proj];//中间辅助数组
int final_solu[num_proj];//结果数组
int max_value=0;//最大价值
void initalize(){
for(int i = 0 ; i < num_proj ; i++ ){
project[i].no = i+1;
project[i].value = value[i];
project[i].weight = weight[i];
project[i].per_value = value[i]/weight[i];
}
}//初始化
bool cmp(treasure a , treasure b){
return a.per_value > b.per_value;
}
//用于使用sort函数,将结构体根据价值密度从大到小排序
int main(){
initalize();
sort(project , project+num_proj , cmp);//排序
cout <<"after sorted by per value, the seq is :";
for(int i = 0 ; i < num_proj ; i++ ){
cout << project[i].no <<" ";
}
cout <<endl;
memset(solution , -1 , num_proj);
//初始化
int cur_weight = 0 , cur_value = 0 , cnt = 0;
for (int j = 0 ; j < num_proj ; j++ ){
if (project[j].weight + cur_weight <= baggage){
cur_weight += project[j].weight;
cur_value += project[j].value;
solution[cnt++] = project[j].no;
//cout << project[j].no<<endl;
}
}
/*根据价值密度,取得当前最佳选择;
如果最佳选择加上当前已有重量超重,那么放弃当前物品,转而寻找下一件;
否则将记录下当前物品的序号,便于输出;
*/
max_value = cur_value;
memset(final_solu,0,num_proj);
for(int k = 0 ; k < num_proj ; k++){
if (solution[k] >= 0 && solution[k] < num_proj){
int temp = solution[k] - 1;
final_solu[temp] = 1;
}
}
/*
中间操作,获取序列
*/
cout<<"solution is : "<<endl;
for(int j = 0;j<num_proj;j++){
cout << final_solu[j]<<" ";
}
cout<<endl<<"max value is "<<max_value<<endl;
//cout<<"hello world";//test*/
}
运行结果:
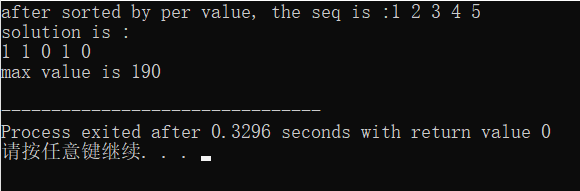
贪心存在的问题:
由于贪心算法总是从局部最优出发,因此往往如前文所述,获得的解仅仅是最优解的一个近似解,上述代码的执行结果恰好说明了这一问题,根据前文的暴力枚举获得的结果,把物品2与物品3放到一起将获得比190更高的价值,而贪心算法的解却无法将该解囊括,因此足以见得,贪心算法虽然简单有效,但也存在结果不精准的缺点,但贪心算法的思想仍然是具有巨大价值的启发式算法。
如何解决贪心缺陷,请听下回分解。
下节预告:k-优化算法,回溯法。
本博客纯属学习总结,希望能起到抛砖引玉的功效,希望各位大佬们能指出我的不足,我将虚心听取。