[数据结构与算法]魔鬼训练 Day 3

1. 将向量下标为偶数的分量 $(x_2,x_4,\dots )$ 累加, 写出相应表达式.

① $$\sum _{i\%2=0}{x}_i$$
② $$\sum _{i=1}^{?2/n?}{x}_{2i}$$

2. 累加习题：求 1! + 2! + 3! + $\dots$ + 20! 。
   $$\sum _{i=1}^{20}i!$$

int sum = 0;
int t = 1;
for(int i = 1; i < 21; i++)
{
	t *= i;
	sum += t;
}

输出：
1!+2!+3!+……+20! = 2561327494111820313

累乘习题：求 1! * 2! * 3! * $\dots$ * 20! 。
$$\prod _{i=1}^{20}i!$$

int res = 1;
int t = 1;
for(int i = 1; i < 21; i++)
{
	t *= i;
	res *= t;
}

积分习题：
$${\int }_1^{20}{x}^3+2dx$$

double integration = 0;
double delta = 0.0001;
for(double x = 1; x <= 20; x += delta)
	integration += (x * x * x + 2) * delta;

3. 三重累加
   三重积分：计算
   $$I=\int \int {\int }_{\Omega }zdv,\Omega :z=\sqrt{x^2+y^2},z=1,z=2$$ 围城的区域。
   
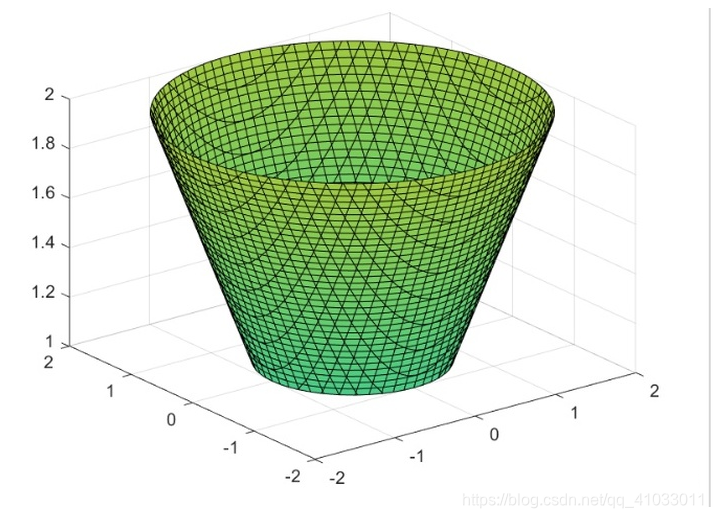
   I = ∫ ∫ ∫ Ω z d v = ∫ 1 2 z d z ∫ ∫ D 1 d x d y D 1 = { ( x , y ) ∣ 0 ≤ x 2 + y 2 ≤ z 2 } I = \int\int\int_{\Omega} zdv = \int_1^2 zdz \int\int_{D_1} dxdy \\ D_1 = \{(x, y) \vert 0 \leq x^2+y^2 \leq z^2\} I=∫∫∫Ω?zdv=∫12?zdz∫∫D1??dxdyD1?={(x,y)∣0≤x2+y2≤z2}
   $$={\int }_1^{2}zdz\int {\int }_{D_1}dxdy={\int }_1^2\pi z^{3}dz=15\pi /4$$

4. 有如下积分。$${\int }_0^{10}x+2dx$$

#include <iostream>
#include <ctime>
using namespace std;

int main()
{
    double integration = 0;
    double delta = 0.0001;;
    clock_t startTime, endTime;
    startTime = clock();//计时开始
    for(double x = 0; x <= 10; x += delta)
        integration += (x + 2) * delta;
    endTime = clock();//计时结束
	cout << integration << endl;
	cout << (double)(endTime - startTime) / CLOCKS_PER_SEC << endl;
}

手算 = 70
程序 = 70.0007

5. 验证最小二乘法见 最小二乘法

6. 逻辑回归推导见 逻辑回归推导